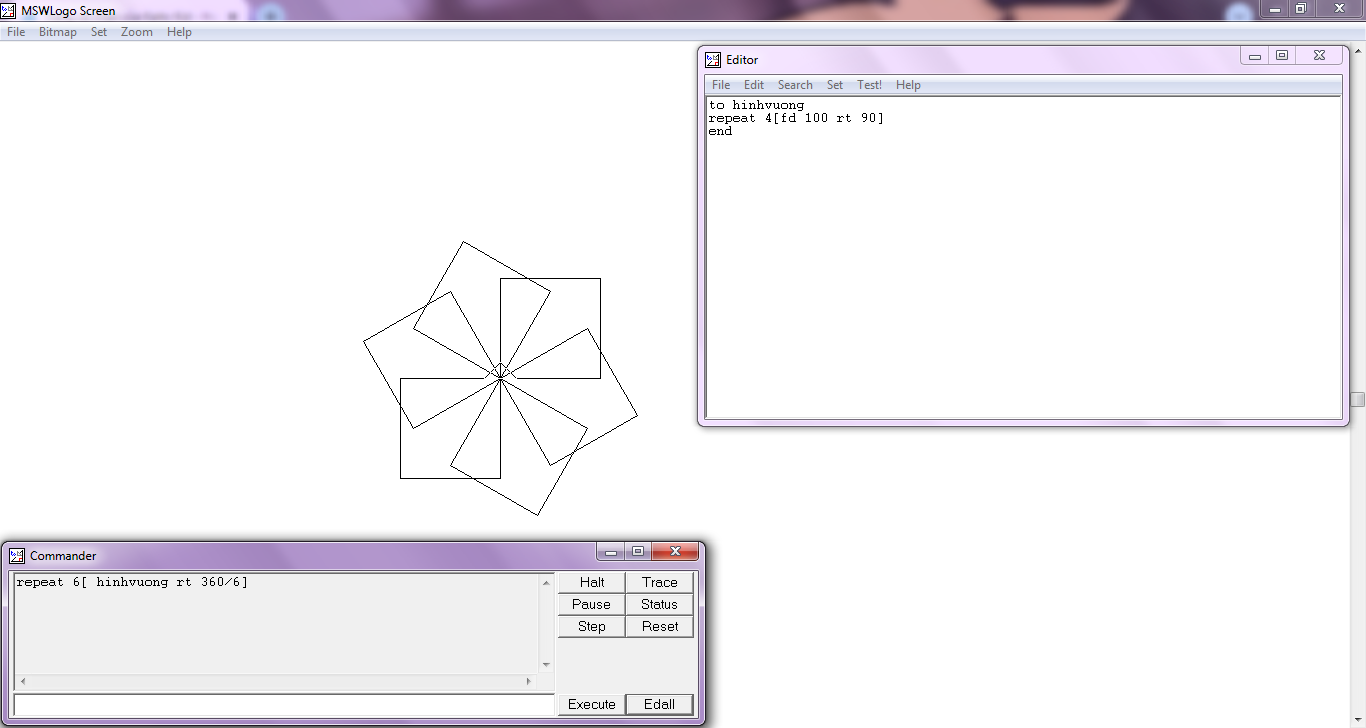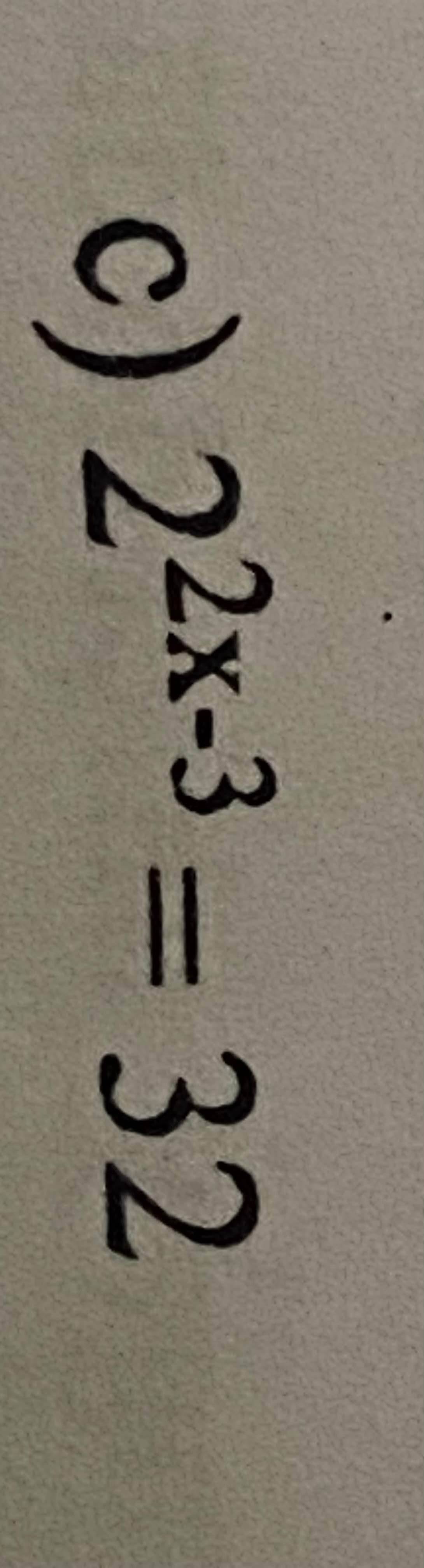
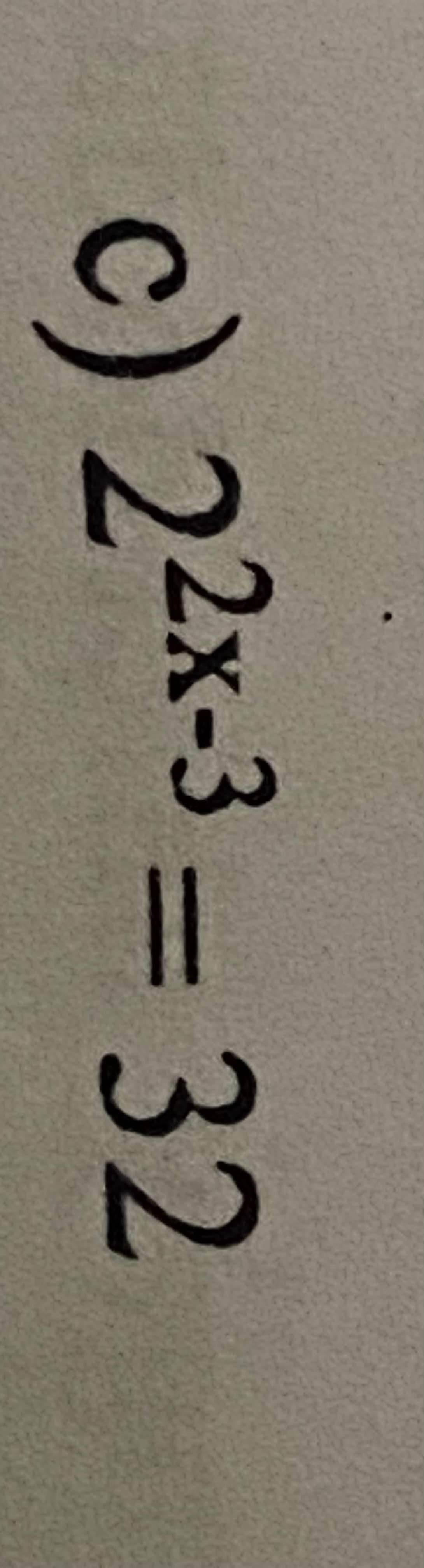 câu này lm thế nào thế ạ
câu này lm thế nào thế ạ

Những câu hỏi liên quan
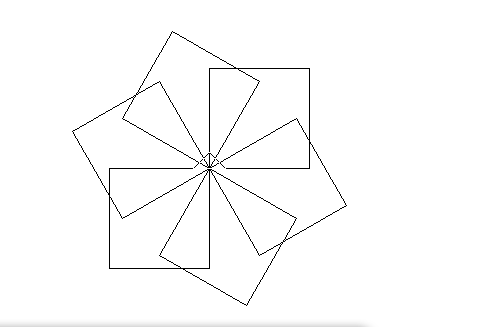
lm thế nào để tạo ra hình này ạ?
Xem thêm câu trả lời
Câu a lm thế nào ạ
a, \(A=\dfrac{7\sqrt{x}+9}{\sqrt{x}+1}=\dfrac{7\left(\sqrt{x}+1\right)+2}{\sqrt{x}+1}=7+\dfrac{2}{\sqrt{x}+1}\)
Ta có : \(\sqrt{x}+1\ge1\Rightarrow\dfrac{2}{\sqrt{x}+1}\le2\)
\(\Rightarrow A=7+\dfrac{2}{\sqrt{x}+1}\le7+2=9\)
Dấu ''='' xảy ra khi x = 0
Vậy GTLN của A bằng 9 tại x = 0
Đúng 1
Bình luận (0)
Câu a lm như thế nào ạ 
Cho mk hỏi câu này lm thế nào
Câu này lm thế nào vậy mọi ngừi?
Did LaToma Tina hold in Spain ?
Mọi người ơi câu 9 và câu 10 lm thế nào vậy ạ ?
câu 9 10 nào hả bạn?
câu này làm như thế nào ạ ?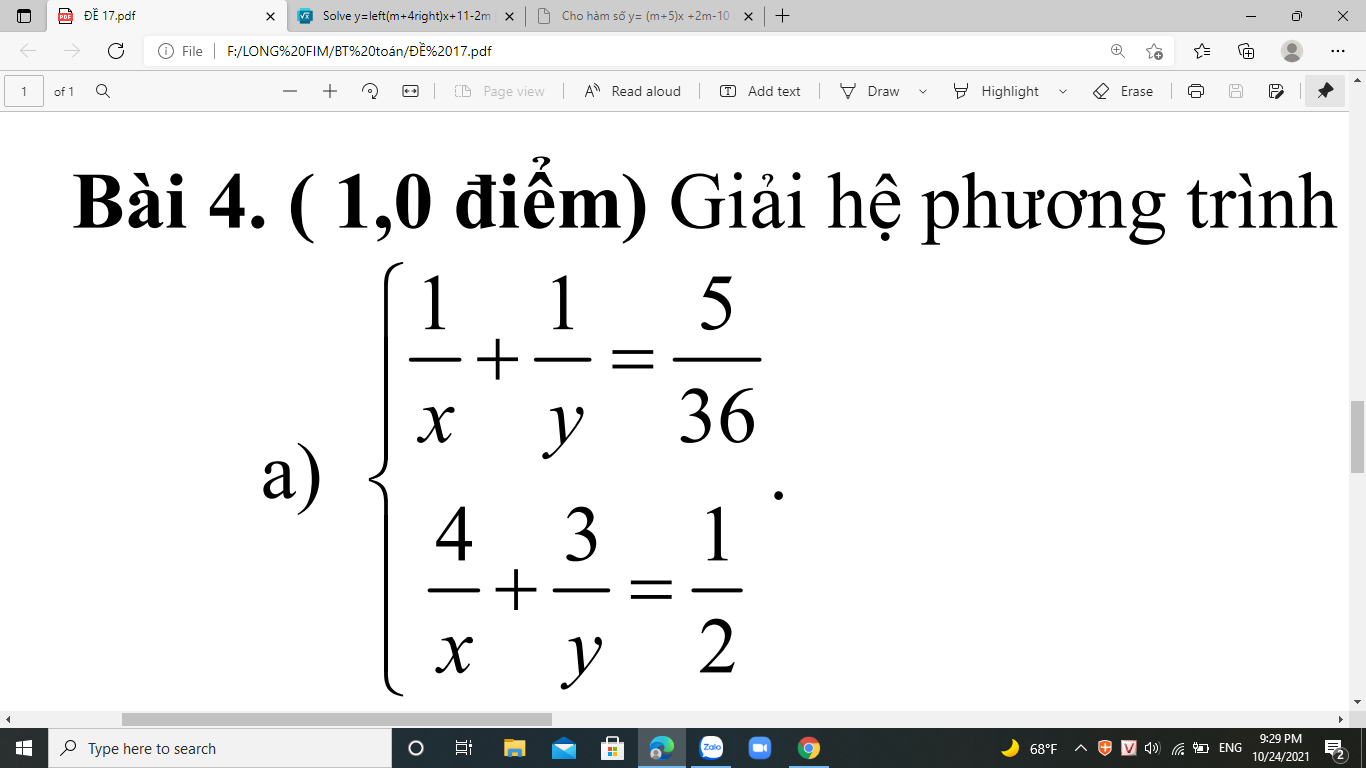
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{36}\\\dfrac{4}{x}+\dfrac{3}{y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{4}{y}=\dfrac{5}{9}\\\dfrac{4}{x}+\dfrac{3}{y}=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1}{18}\\\dfrac{1}{x}=\dfrac{1}{36}-\dfrac{1}{18}=-\dfrac{1}{36}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=18\\x=-36\end{matrix}\right.\)
Đúng 0
Bình luận (0)
 giải câu này như thế nào ạ
giải câu này như thế nào ạ
Câu này giải như thế nào ạ
a. \(C=\dfrac{n+1}{n-2}\) \(\left(n\ne2\right)\)
\(C=\dfrac{n-2+3}{n-2}=\dfrac{n-2}{n-2}+\dfrac{3}{n-2}=1+\dfrac{3}{n-2}\)
Để C nguyên thì \(\dfrac{3}{n-2}\in Z\) \(\Leftrightarrow n-2\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
`@n-2=1->n=3(n)`
`@n-2=-1->n=1(n)`
`@n-2=3->n=5(n)`
`@n-2=-3->n=-1(n)`
Vậy \(n\in\left\{3;1;5;-1\right\}\) thì C nguyên
b.\(D=\dfrac{2n+1}{5n-3}\left(n\ne\dfrac{3}{5}\right)\)
Ta có: \(2n+1⋮5n-3\)
\(\Leftrightarrow5.\left(2n+1\right)⋮\left(5n-3\right)\)
\(\Leftrightarrow10n+5⋮5n-3\)
\(\Leftrightarrow2\left(5n-3\right)+11⋮\left(5n-3\right)\)
Vì \(2\left(5n-3\right)⋮\left(5n-3\right)\) nên để D nguyên thì \(11⋮\left(5n-3\right)\)
hay \(5n-3\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
`@5n-3=1->n=14/5(l)`
`@5n-3=-1->n=2/5(l)`
`@5n-3=11->n=14/5(l)`
`@5n-3=-11->n=-8/5(l)`
Vậy không có giá trị \(n\in Z\) thỏa mãn
Đúng 1
Bình luận (0)