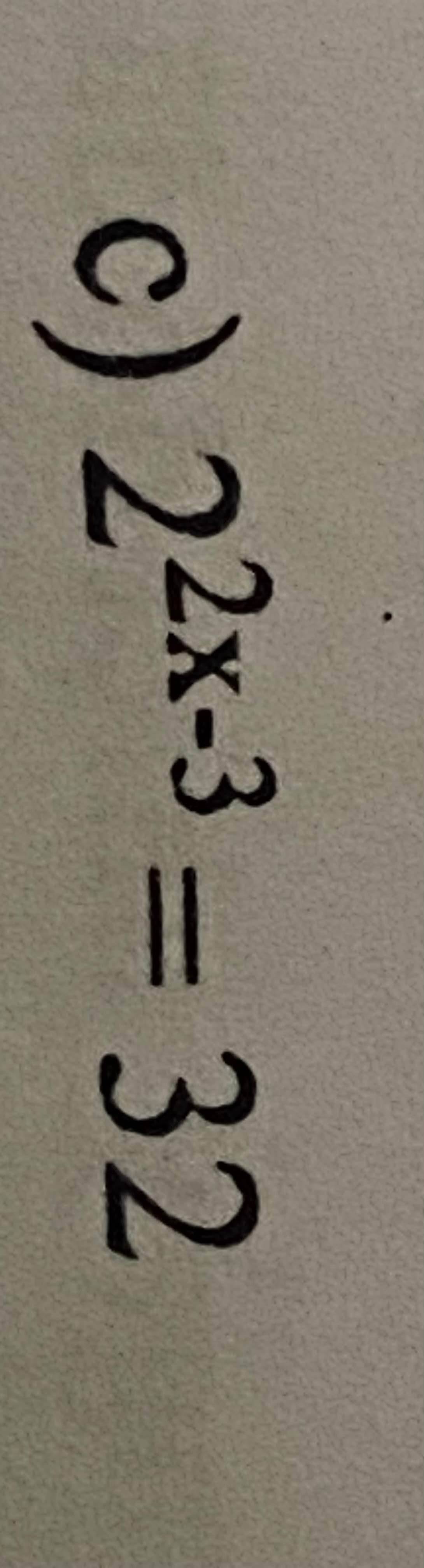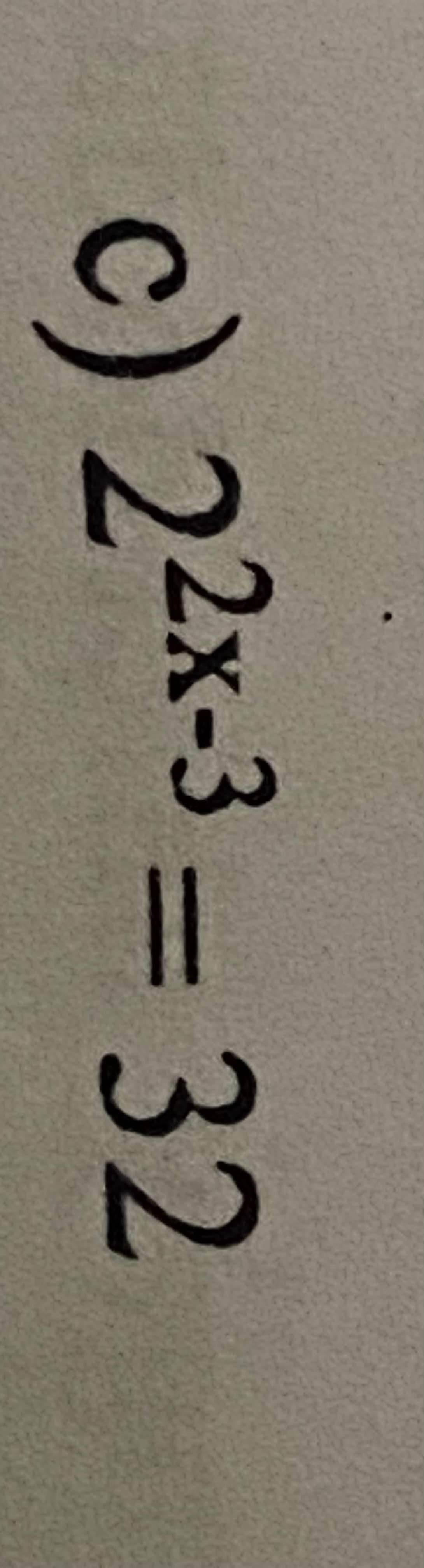a. \(C=\dfrac{n+1}{n-2}\) \(\left(n\ne2\right)\)
\(C=\dfrac{n-2+3}{n-2}=\dfrac{n-2}{n-2}+\dfrac{3}{n-2}=1+\dfrac{3}{n-2}\)
Để C nguyên thì \(\dfrac{3}{n-2}\in Z\) \(\Leftrightarrow n-2\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
`@n-2=1->n=3(n)`
`@n-2=-1->n=1(n)`
`@n-2=3->n=5(n)`
`@n-2=-3->n=-1(n)`
Vậy \(n\in\left\{3;1;5;-1\right\}\) thì C nguyên
b.\(D=\dfrac{2n+1}{5n-3}\left(n\ne\dfrac{3}{5}\right)\)
Ta có: \(2n+1⋮5n-3\)
\(\Leftrightarrow5.\left(2n+1\right)⋮\left(5n-3\right)\)
\(\Leftrightarrow10n+5⋮5n-3\)
\(\Leftrightarrow2\left(5n-3\right)+11⋮\left(5n-3\right)\)
Vì \(2\left(5n-3\right)⋮\left(5n-3\right)\) nên để D nguyên thì \(11⋮\left(5n-3\right)\)
hay \(5n-3\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
`@5n-3=1->n=14/5(l)`
`@5n-3=-1->n=2/5(l)`
`@5n-3=11->n=14/5(l)`
`@5n-3=-11->n=-8/5(l)`
Vậy không có giá trị \(n\in Z\) thỏa mãn