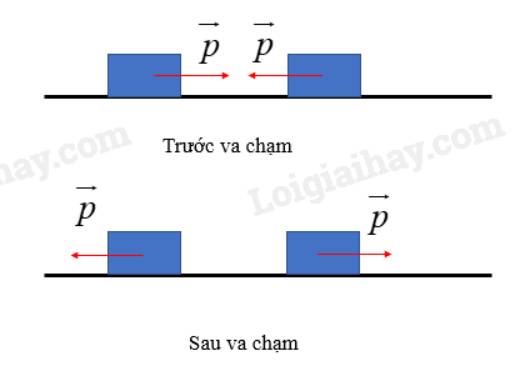
Đánh giá sự thay đổi động lượng của từng xe và cả hệ trước và sau va chạm.

Những câu hỏi liên quan
8. Đánh giá sự thay đổi động lượng của từng xe và cả hệ trước và sau va chạm.
Đánh giá sự thay đổi năng lượng (thông qua động năng) của hệ trong hai va chạm đang xét.
Từ bảng tính toán số liệu, ta thấy:
+ Va chạm đàn hồi: Động năng của hệ trước và sau va chạm gần bằng nhau.
+ Va chạm mềm: Động năng của hệ sau va chạm nhỏ hơn động năng của hệ trước va chạm.
Đúng 0
Bình luận (0)
10. Đánh giá sự thay đổi năng lượng (thông qua động năng) của hệ trong hai va chạm đang xét.
Từ bảng tính toán số liệu, ta thấy:
+ Va chạm đàn hồi: Động năng của hệ trước và sau va chạm gần bằng nhau.
+ Va chạm mềm: Động năng của hệ sau va chạm nhỏ hơn động năng của hệ trước va chạm.
Đúng 0
Bình luận (0)
Từ kết quả thí nghiệm của mình, bạn hãy tính động lượng của các xe trước và sau va chạm. So sánh độ thay đổi động lượng của xe 1 và xe 2.

Khối lượng của hai xe là như nhau và đều có độ lớn là m = 0,245 (kg)
Động lượng của xe 1 trước va chạm: p1 = 0,444.m
Động lượng của xe 1 sau va chạm: p’1 = 0,316.m
=> Độ thay đổi động lượng của xe 1 là: \(\Delta {p_1} = \left| {p_1' - {p_1}} \right| = 0,444m - 0,316m \approx 0,03(kg.m/s)\)
Động lượng của xe 2 trước va chạm: p2 = 0,316.m
Động lượng của xe 2 sau va chạm: p’2 = 0,438.m
=> Độ thay đổi động lượng của xe 2 là: \(\Delta {p_2} = \left| {p_2' - {p_2}} \right| = 0,438m - 0,316m \approx 0,03(kg.m/s)\)
=> Độ thay đổi động lượng của xe 1 và xe 2 bằng nhau.
Đúng 0
Bình luận (0)
Hãy biểu diễn độ thay đổi động lượng của từng xe sau khi va chạm (hình 1.2)
Một quả cầu A khối lượng 2 kg chuyển động trên máng thẳng ngang không ma sát với vận tốc 3 m/s và tới va chạm vào quả cầu B khối lượng 3 kg đang chuyển động với vận tốc 1 m/s cùngchiều với quả cầu A trên cùng một máng ngang. Xác định độ lớn của vận tốc và chiều chuyển động của hai quả cầu sau khi va chạm. Cho biết sự va chạm giữa hai quả cầu A và B có tính chất hoàn toàn đàn hồi, tức là sau khi va chạm thì các quả cầu này chuyển động tách rời khỏi nhau, đồng thời tổng động năng của chúng trước v...
Đọc tiếp
Một quả cầu A khối lượng 2 kg chuyển động trên máng thẳng ngang không ma sát với vận tốc 3 m/s và tới va chạm vào quả cầu B khối lượng 3 kg đang chuyển động với vận tốc 1 m/s cùng'chiều với quả cầu A trên cùng một máng ngang. Xác định độ lớn của vận tốc và chiều chuyển động của hai quả cầu sau khi va chạm. Cho biết sự va chạm giữa hai quả cầu A và B có tính chất hoàn toàn đàn hồi, tức là sau khi va chạm thì các quả cầu này chuyển động tách rời khỏi nhau, đồng thời tổng động năng của chúng trước và sau va chạm được bảo toàn (không thay đổi).
Chọn chiều chuyển động ban đầu của quả cầu A là chiều dương. Hệ vật gồm hai quả cầu A và B. Gọi v 1 , v 2 và v ' 1 , v ' 2 là vận tốc của hai quả cầu trước và sau khi va chạm.
Vì hệ vật chuyển động không ma sát và ngoại lực tác dụng lên hệ vật (gồm trọng lực và phản lực của máng ngang) đều cân bằng nhau theo phương thẳng đứng, nên tổng động lượng của hệ vật theo phương ngang được bảo toàn (viết theo trị đại số):
m 1 v ' 1 + m 2 v ' 2 = m 1 v 1 + m 2 v 2
2. v ' 1 + 3. v ' 2 = 2.3 +3.1 = 9
Hay v ' 1 + 1,5. v ' 2 = 4,5 ⇒ v ' 2 = 3 - 2 v ' 1 /3 (1)
Đồng thời, tổng động năng của hệ vật cũng bảo toàn, nên ta có:
m1 v ' 1 2 /2 + m2 v ' 2 2 /2 = m1 v 1 2 /2 + m2 v 2 2 /2
2 v ' 1 2 /2 + 3 v ' 2 2 /2 = 2. 3 2 /2 + 3. 1 2 /2
Hay v ' 1 2 + 1,5 v ' 2 2 = 10,5 ⇒ v ' 2 2 = 7 - 2 v ' 1 2 /3 (2)
Giải hệ phương trình (1), (2), ta tìm được: v ' 1 = 0,6 m/s; v ' 2 = 2,6 m/s
(Chú ý: Loại bỏ cặp nghiệm v ' 1 = 3 m/s, v ' 2 = 1 m/s, vì không thỏa mãn điều kiện v ' 2 > v 2 = 1 m/s)
Đúng 0
Bình luận (0)
Một quả bóng bida khối lượng 0,35 kg va chạm vuông góc vào mặt bên của mặt bida và bật ra cũng vuông góc. Tốc độ của nó trước khi va chạm là 2,8 m/s và tốc độ sau khi va chạm là 2,5 m/s. Tính độ thay đổi động lượng của quả bida.
Độ thay đổi động lượng của quả bida là:
\(\Delta p = \left| {{p_s} - {p_{tr}}} \right| = \left| {m.{v_s} - m.{v_{tr}}} \right| = \left| {0,25(2,5 - 2,8)} \right| = 0,075(kg.m/s)\)
Đúng 0
Bình luận (0)
8. Từ kết quả thí nghiệm, hãy tính độ chênh lệch tương đối động lượng của hệ trước và sau va chạm \(\dfrac{\left|p_1-p^,\right|}{p_1}.100\%\) Từ đó, nêu nhận xét về động lượng của hệ trước và sau va chạm.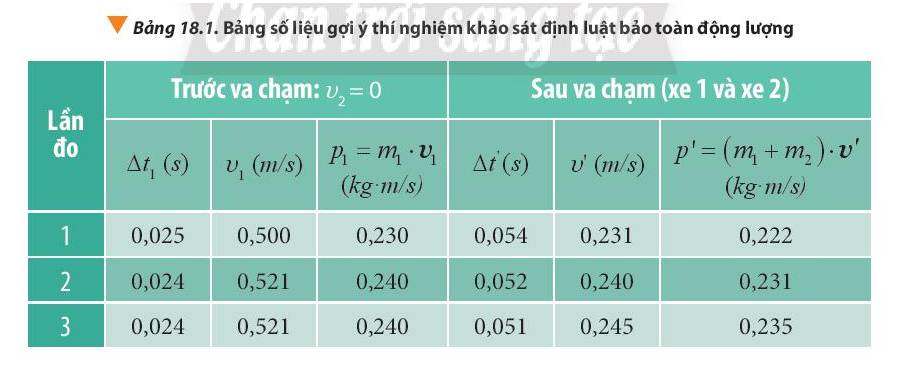
Câu 11. Trong thí nghiệm xác định động lượng của vật trước và sau va chạm để đo tốc độ của hai xe trước và sau va chạm ta làm cách nào sau đây?A. Do thời gian, sau đó tính gián tiếp tốc độ và động lượng của vật trước và sau va chạm.B. Đo trực tiếp tốc độ sau đó tính gián tiếp động lượng của vật trước và sau va chạm.C. Đo trực tiếp động lượng của vật trước và sau va chạm.D. Chỉ cần đo thời gian là kết luận được.
Đọc tiếp
Câu 11. Trong thí nghiệm xác định động lượng của vật trước và sau va chạm để đo tốc độ của hai xe trước và sau va chạm ta làm cách nào sau đây?
A. Do thời gian, sau đó tính gián tiếp tốc độ và động lượng của vật trước và sau va chạm.
B. Đo trực tiếp tốc độ sau đó tính gián tiếp động lượng của vật trước và sau va chạm.
C. Đo trực tiếp động lượng của vật trước và sau va chạm.
D. Chỉ cần đo thời gian là kết luận được.