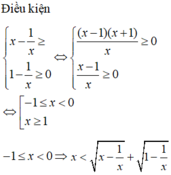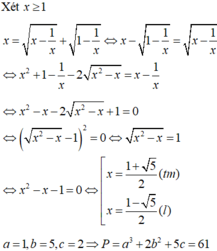Những câu hỏi liên quan
cho 3 số a,b,c khác 0 thỏa mãn : a/b + b/c + c/a = b/a + a/c + c/b. tính giá trị của biểu thức p = (a - b) (b - c) (c - a) (a + 2b + 3c) 2022 + 2023
2.Cho a, b, c là các số thực khác 0 thỏa a ^ 2 + b ^ 2 + c ^ 2 = ab + bc + ca . Tính giá trị của biểu thúc T = (a ^ 2022 + b ^ 2022 + c ^ 2022)/((a + b + c) ^ 2022)
a^2+b^2+c^2=ab+bc+ac
=>2a^2+2b^2+2c^2-2ab-2bc-2ac=0
=>a^2-2ab+b^2+b^2-2bc+c^2+a^2-2ac+c^2=0
=>(a-b)^2+(b-c)^2+(a-c)^2=0
=>a=b=c
\(T=\dfrac{a^{2022}+a^{2022}+a^{2022}}{\left(3a\right)^{2022}}=\dfrac{3}{3^{2022}}=\dfrac{1}{3^{2021}}\)
Đúng 3
Bình luận (0)
Cho a,b,c khác 0 từ x=a+b/c=b+c/a=c+a/b.Tính giá trị biểu thức P=(x-1)^2022
cho các số hữu tỉ a,b,c khác 0 sao cho: \(\frac{5a+5b-c}{c}=\frac{5b+5c-a}{a}=\frac{5c+5a-b}{b}\)
tính giá trị của biểu thức : P = \(\frac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{16120abc}\)
Cho các số hữu a,b,c khác 0 sao cho : \(\frac{5a+5b-c}{c}=\frac{5b+5c-a}{a}=\frac{5c+5a-b}{b}\)
Tinghs giá trị biểu thức: \(P=\frac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{16120abc}\)
\(\frac{5a+5b-c}{c}=\frac{5b+5c-a}{a}=\frac{5c+5a-b}{b}\)
\(\Leftrightarrow\)\(\frac{5a+5b-c}{c}+1=\frac{5b+5c-a}{a}+1=\frac{5c+5a-b}{b}+1\)
\(\Leftrightarrow\)\(\frac{5a+5b}{c}=\frac{5b+5c}{a}=\frac{5c+5a}{b}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{5a+5b}{c}=\frac{5b+5c}{a}=\frac{5c+5a}{b}=\frac{5a+5b+5b+5c+5c+5a}{a+b+c}=\frac{10\left(a+b+c\right)}{a+b+c}=10\)
Do đó :
\(\frac{5a+5b}{c}=10\)\(\Leftrightarrow\)\(5a+5b=10c\)\(\Leftrightarrow\)\(a+b=2c\) \(\left(1\right)\)
\(\frac{5b+5c}{a}=10\)\(\Leftrightarrow\)\(5b+5c=10a\)\(\Leftrightarrow\)\(b+c=2a\) \(\left(2\right)\)
\(\frac{5c+5a}{b}=10\)\(\Leftrightarrow\)\(5c+5a=10b\)\(\Leftrightarrow\)\(c+a=2b\) \(\left(3\right)\)
Thay (1), (2) và (3) vào \(P=\frac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{16120abc}\) ta được :
\(P=\frac{2c.2a.2b}{16120abc}=\frac{8abc}{16120abc}=\frac{1}{2015}\)
Vậy \(P=\frac{1}{2015}\)
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
a/3 - b=c:3/5 và a b c khác 0 tính Q=2022-(a-5c/5a)^3.(a-3b/b)^3.(5c+3b/3c)^3
\(\frac{a}{3}-b=c:\frac35\)
=>\(\frac{a-3b}{3}=c\cdot\frac53=\frac{5c}{3}\)
=>a-3b=5c
=>a-5c=3b; 5c+3b=a
\(\left(\frac{a-5c}{5a}\right)^3=\left(\frac{3b}{5a}\right)^3=\frac{27b^3}{125a^3}\)
\(\left(\frac{a-3b}{b}\right)^3=\left(\frac{5c}{b}\right)^3=\frac{125c^3}{b^3}\)
\(\left(\frac{5c+3b}{3c}\right)^3=\left(\frac{a}{3c}\right)^3=\frac{a^3}{27c^3}\)
\(Q=2022-\left(\frac{a-5c}{5a}\right)^3\cdot\left(\frac{a-3b}{b}\right)^3\cdot\left(\frac{5c+3b}{3c}\right)^3\)
\(=2022-\frac{27b^3}{125a^3}\cdot\frac{125c^3}{b^3}\cdot\frac{a^3}{27c^3}=2022-1=2021\)
Đúng 0
Bình luận (0)
Giải phương trình:
x
x
-
1
x
+
1
-
1
x
ta được một nghiệm
x
a
+
b
c
,
a
,
b
,
c
∈
ℕ
;
b...
Đọc tiếp
Giải phương trình: x = x - 1 x + 1 - 1 x ta được một nghiệm x = a + b c , a , b , c ∈ ℕ ; b < 20 . Tính giá trị biểu thức P = a 3 + 2 b 2 + 5 c .
A. P = 61
B. P = 109
C. P = 29
D. P = 73
Cho 3 số thực a,b,c khác 0 và đôi một khác nhau thỏa mãn \(a^2\left(b+c\right)=b^2\left(a+c\right)=2022\).Tính giá trị của iểu thức P= \(c^2\left(a+b\right)\)
`Answer:`
Có `a^2.(b+c)=b^2.(a+c)`
`<=>a^2.b+a^2.c-ab^2-b^2.c=0`
`<=>ab.(a-b)+c.(a^2-b^2)=0`
`<=>(a-b)(ab+c(a+b))=0`
`<=>(a-b)(ab+ac+bc)=0`
`<=>ab+ac+bc=0`
Lúc này `P=c^2.(a+b)=c.(ac+bc)=c.(-ab)=-abc`
Mà `a^2.(b+c)=a.(ab+ac)=a.(-bc)=-abc=2022`
Vậy `P=2022`
cho biết a/2 -b=c:2/3 và a,b,c khác 0. tính giá trị biểu thức Q=2018 - (c/a - 1/3)^5 x . (a/2 - 2) ^5 . (3/2 + b/c )^5
Bạn cần viết đề bài bằng công thức toán để được hỗ trợ tốt hơn (biểu tượng $\sum$ bên trái khung soạn thảo)
Đúng 1
Bình luận (0)