Trên cạnh AB ở phía trong hình vuông ABCD dựng tam giác AFB cân tại F có góc đáy là 15 độ. Chứng minh tam giác CFD đều.

Những câu hỏi liên quan
1.trên cạnh AB ở phía trong hình vuông ABCD dựng tam giác AFB cân, đỉnh F có góc đáy là 15 độ.Cm tam giác CFD là tam giác đều
2.Trong tam giác ABC lấy P sao cho góc PAC = góc PBC.Từ P dựng PM vuông góc vs BC,PK vuông góc vs CA.Gọi D là trung điểm của AB.CM DK=DM
Ở phía trong hình vuông ABCD dựng tam giác ABE cân tại E có góc đáy 15o. Chứng minh rằng tam giác CDE đều
Phía trong của hình vuông ABCD ta dựng tam giác đều ADK. Ta có AD = AK = DK.
\(\widehat{DAK}=90^o-\widehat{KAD}=30^o\).
Do AB = AK (cùng bằng AD) nên tam giác BAK cân tại A.
Suy ra \(\widehat{ABK}=\widehat{AKB}=\frac{180^o-\widehat{BAK}}{2}=75^o\).
Suy ra \(\widehat{BKC}=90^o-\widehat{ABK}=15^o\).
Tương tự ta cũng có \(\widehat{KDC}=30^o,\widehat{DCK}=75^o,\widehat{KCB}=15^o\).
Dễ dàng chứng minh được \(\Delta ABE=\Delta BKC\left(g.c.g\right)\) nên AE = BE = BK = KC.
Từ đó ta chứng minh được \(\Delta AED=\Delta CDK\left(c.g.c\right)\).
Suy ra \(\widehat{ADE}=\widehat{KDC}=30^o\).
Suy ra tam giác CDE đều.
Đúng 1
Bình luận (0)
Bài 143. Ở phía trong hình vuông ABCD, vẽ tam giác ADE cân ở E có góc đáy bằng 15 độ.
a) Chứng minh tam giác BEC đều.
b) Ở phía ngoài hình vuông ABCD, vẽ tam giác DCF đều. Chứng minh A, E, F thẳng hàng.
Cho hình vuông ABCD, về phía trong hình vuông, dựng tam giác ABE cân tại E có góc đáy 15 độ. Chứng minh rằng tam giác CDE đều.
Mọi người giúp em với ạ! Em cảm ơn!
Cho hình vuông ABCD. Về phía trong của hình vuông dựng tam giác cân FAB (FA = FB) sao cho góc FAB = 15 độ. Chứng minh tam giác FCD đều.
Bài này khó đó bạn, có lẽ phải vẽ thêm đường phụ
Đúng 0
Bình luận (0)
Có hai cách vẽ thêm hình phụ ở bài này:
Dựng tam giác đều IFB, I nằm trong tam giác CFB.
Hoặc ở phía ngoài hình vuông ABCD dựng tam giác ABH đều.
Đúng 0
Bình luận (0)
1.Cho tam giác đều BSC, phía trong tam giác vẽ tam giác vuông cân ABC.trong tam giác abc lấy điểm D sao cho góc DBC=ACD=30 độ. Chứng minh tứ giác SADC là hình thang
2.Cho hình thang vuông ABCD (góc C=B=90 độ). Có AB=Bc=1/2 DC. Lấy điểm M bất kì trên cạnh AB, lấy điểm N trên cạnh AD sao cho góc NMC=90 độ. Chứng minh rằng khi M thay đổi trên cạnh AB thì góc MNC có số đo không đổi.
cho hình vuông ABCD có điểm O thuộc hình vuông ,sao cho tam giác DOC cân ở O và góc ở đáy bằng 15 độ . Chứng minh tam giác AOB đều .
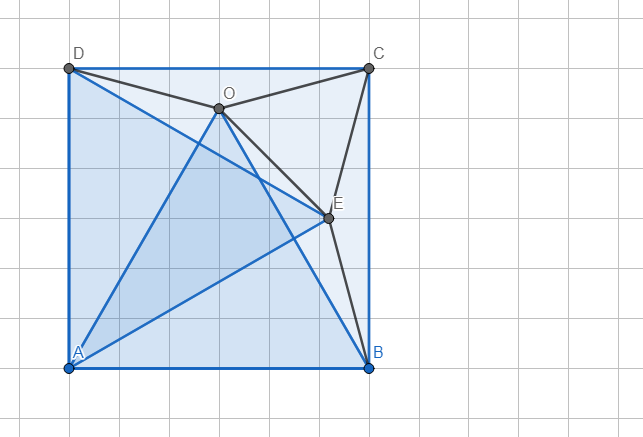
*Dựng △ADE đều.
\(\widehat{ODC}=\widehat{OCD}=15^0\Rightarrow\)△DOC cân tại O.
\(\Rightarrow OD=OC;\widehat{DOC}=180^0-2\widehat{ODC}=180^0-2.15^0=150^0\)
\(\widehat{BAE}=\widehat{CDE}=90^0-\widehat{ADE}=90^0-60^0=30^0\)
\(AB=AE=DE=DC=AD\).
\(\Rightarrow\)△DCE cân tại D, △ABE cân tại A.
\(\Rightarrow\widehat{DCE}=\widehat{ABE}=\dfrac{180^0-\widehat{BAE}}{2}=\dfrac{180^0-30^0}{2}=75^0\).
\(\Rightarrow\widehat{ECB}=\widehat{EBC}=90^0-\widehat{DCE}=90^0-75^0=15^0\)
\(\widehat{OCE}=90^0-\widehat{OCD}-\widehat{BCE}=90^0-15^0-15^0=60^0\)
△DOC và △BEC có: \(\widehat{ODC}=\widehat{EBC}=15^0;\widehat{OCD}=\widehat{ECB}=15^0;DC=BC\)
\(\Rightarrow\)△DOC=△BEC (g-c-g)
\(\Rightarrow OD=BE=OC=EC\)
\(\Rightarrow\)△OCE cân tại C mà \(\widehat{OCE}=60^0\)
\(\Rightarrow\)△OCE đều.
\(\widehat{OEB}=360^0-\widehat{OEC}-\widehat{BEC}=360^0-60^0-150^0=150^0\)
\(OE=CE=EB\Rightarrow\)△OEB cân tại E.
\(\Rightarrow\widehat{OBE}=\dfrac{180^0-\widehat{OEB}}{2}=\dfrac{180^0-150^0}{2}=15^0\)
\(\widehat{OBA}=90^0-\widehat{OBE}-\widehat{CBE}=90^0-15^0-15^0=60^0\)
Mà △OAB cân tại O \(\Rightarrow\)△OAB đều.
Đúng 4
Bình luận (0)
ai làm giúp mình bài này với ạ,mình cảm ơn!
cho đoạn thẳng AB,trên cùng một nửa mặt phẳng bờ AB vẽ hình vuông ABCD và tam giác ABE cân có đáy AB,góc ở đáy bằng 15 độ.Vẽ tam giác AEF đều (F và D cùng phía đối với AE):a)Tính góc AFD?b)Tính góc EFD?c)Tính góc DEC
Cho hình thang cân ABCD có đáy lớn CD bằng 2 lần cạnh bên BC. Về bên ngoài hình thang dựng các tam giác đều ADF và BCE. G là trung điểm của CD. a) Chứng minh rằng tam giác EGF cân. b) Biết tam giác EFG vuông, AB = a. Tính các góc và các cạnh của hình thang.














