cho hình vẽABDCcdaCM a//d. Biết góc ADC65 độtính góc x?
Đọc tiếp
cho hình vẽ
CM a//d. Biết góc ADC=65 độ
tính góc x?
Những câu hỏi liên quan
Cho hình vẽ, biết góc A = 20 độ; góc C = 25 độ; góc B = 50 độ
Tính góc ADC.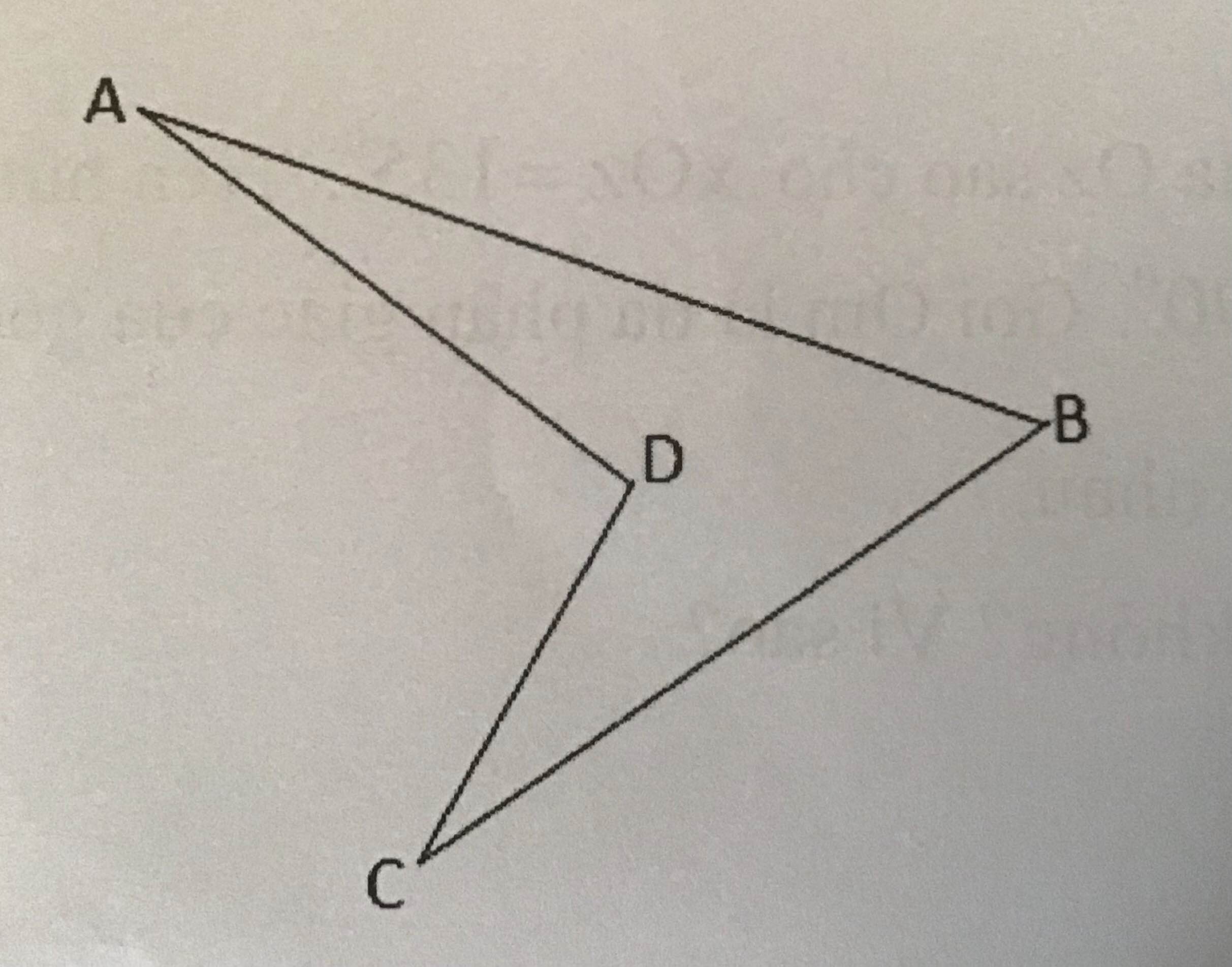
Xét tam giác ABC có \(\widehat{BAC}+\widehat{ACB}+\widehat{B}=180\Rightarrow\widehat{BAD}+\widehat{DAC}+\widehat{ACD}+\widehat{BAD}+\widehat{B}=180\) độ
hay \(20+\widehat{DAC}+25+\widehat{ACD}+50=180\) độ
\(\Rightarrow\widehat{DAC}+\widehat{ACD}=85\) độ
Xét tam giác ADC có \(\widehat{DAC}+\widehat{ACD}+\widehat{ADC}=180\Rightarrow\widehat{ADC}=180-85=95\) độ
Tick hộ nha
Đúng 3
Bình luận (0)
Một hình thang cân có 1 góc nhọn bằng 65 độtính các góc còn lại của hình thang cân
cho hình thang ABCD co góc A =3 lần góc D; góc B-góc C=40 độtính các goc của hình thang
Cho tam giác ABC biết góc A + góc B = 120 độ và góc A - góc B = 30 độ
Tính số đo các góc cuat tam giác ABC
Số đo `hat(A)=(120^0+30^0)/2=75^0`
Số đo `hat(B)=120^0-75^0=45^0`
`Delta ABC` có `hat(A)+hat(B)+hat(C)=180^0`
`=>(hat(A)+hat(B))+hat(C)=180^0`
hay `120^0+hat(C)=180^0`
`=>hat(C)=180^0-120^0=60^0`
Vậy ...
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC có AD, BE lần lượt là tia phân giác trong các góc A, B (D∈ BC; E∈ CA). Biết AD cắt Be tại K và góc ABK= 110 độ; góc KAC= 30 độ
Tính số đo cá góc A,B,C của tam giác ABC.
Bài 1: Cho tam giác ABC có AD, BE lần lượt là tia phân giác trong các góc A, B (D∈ BC; E∈ CA). Biết AD cắt Be tại K và góc ABK= 110 độ; góc KAC= 30 độ
Tính số đo cá góc A,B,C của tam giác ABC.
Đề sai rồi bạn:
Nếu BK là p/g thì \(\widehat{B}=2\widehat{ABK}=220^0\)(vô lí)
Đúng 1
Bình luận (0)
Bài 1 : Cho hình thang ABCD ( AB // CD ) có góc A bằng 3 lần góc B ; góc C 160độ.Tính các góc còn lạiBài 2 : Cho hình thang cân ABCD ( AB// CD ) có AD BC x cm ( x chưa biết ) và góc ADC bằng 60độ . DB là đường phân giác góc ADCa) Tính góc DAB và góc DBCb) Tính cạnh AB và CD theo xc) Gọi M là trung điểm CD . Chứng minh tam giác AMD đềud) Chứng minh rằng MA là đường trung trực của BD
Đọc tiếp
Bài 1 : Cho hình thang ABCD ( AB // CD ) có góc A bằng 3 lần góc B ; góc C = 160độ.Tính các góc còn lại
Bài 2 : Cho hình thang cân ABCD ( AB// CD ) có AD = BC = x cm ( x chưa biết ) và góc ADC bằng 60độ . DB là đường phân giác góc ADC
a) Tính góc DAB và góc DBC
b) Tính cạnh AB và CD theo x
c) Gọi M là trung điểm CD . Chứng minh tam giác AMD đều
d) Chứng minh rằng MA là đường trung trực của BD
Cho tứ giác ABCD có AB song song CD, Cx là tia đối của tia CD, biết góc ADC=65°; BCx=130°. Tính số đo góc A, Góc B của tứ giác
Cho hình thang ABCD có đáy AB và CD biết góc A =65° , góc C =90°.Tính góc B,D?
\(\widehat{D}=115^0\)
\(\widehat{B}=90^0\)
Đúng 0
Bình luận (0)