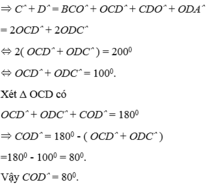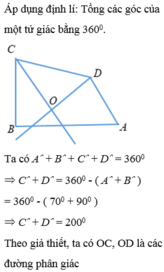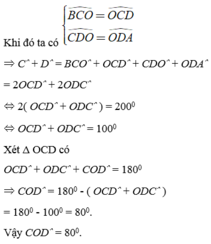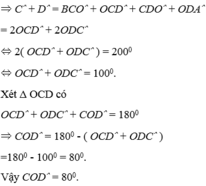Cho tứ giác ABCD có A=70o,B=100o,các tia phân giác của góc C và D cắt nhau tại O.Tính số đo COD

Những câu hỏi liên quan
Cho tứ giác ABCD có A ^ = 70 0 , B ^ = 90 0 . Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc C O D ^ ?
Cho tứ giác ABCD có A ^ = 70 0 , B ^ = 90 0 . Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc C O D ^ ?
Cho tứ giác ABCD có A ^ = 70 0 , B ^ = 90 0 . Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc C O D ^ ?
Tứ giác ABCD có A = 101o, B = 100o. Các tia phân giác của các góc C và D cắt nhau ở E. Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau tại F. Tính góc (CED) ,(CFD) .
Bạn tham khảo tại đây:
Bài 8 Sách bài tập - trang 80 - Toán lớp 8 | Học trực tuyến
Bạn chú ý cái đường link rồi sửa thành h là OK hết chỗ nói nha.Hoặc là ib với mik rồi mik cho:3
Đúng 0
Bình luận (0)
Bạn tham khảo nhé :
https://h.o.c24.vn/hoi-dap/question/255576.html
~Std well~
#Thạc_Trân
Đúng 0
Bình luận (0)
Trong tứ giác ABCD, ta có: ∠A + ∠B + ∠C + ∠D = 360o
⇒ ∠C + ∠D = 360o - (∠A + ∠B) = 360o – (110o + 100o) = 150o
\(\widehat{C_1}+\widehat{D_1}=\frac{\widehat{C}+\widehat{D}}{2}=\frac{150}{2}=75o.\)
Trong ΔCED ta có:
∠CED = 180o – (∠C1 + ∠D1) = 180o – 75o = 105o
DE ⊥ DF (t/chất tia phân giác của hai góc kề bù) ⇒ ∠EDF = 90o
CE ⊥ CF (t/chất tia phân giác của hai góc kề bù) ⇒ ∠ECF = 90o
Trong tứ giác CEDF, ta có: ∠DEC + ∠EDF + ∠DFC + ∠ECF = 360o
⇒ ∠DFC = 360o - (∠DEC + ∠EDF + ∠ECF) = 75o
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 3: Cho tứ giác ABCD có AB//CD và góc D =60 độ
a) Tính số đo góc A?
b) Biết góc B phần góc D = 4/5. Tính góc B, góc C
Bài 4: Cho tứ giác ABCD, góc A - góc B = 40 độ. Các tia phân giác của góc C, góc D cắt nhau tại O. Cho biết góc COD= 110 độ. Chứng minh rằng AB vuông góc với BC
Nhờ các bạn hướng dẫn mình hai bài này
a) Vì AB//CD, ta có góc ACD = góc BCD = 180 - góc D = 180 - 60 = 120 độ.
Vì AB//CD, ta có góc ACD = góc BAD.
Vậy số đo góc A là 120 độ.
b) Gọi góc BCD là x độ.
Theo giả thiết, góc B phần góc D = 4/5, ta có:
góc B = (4/5) * góc D
= (4/5) * 60
= 48 độ.
Vì AB//CD, ta có góc BCD = góc BAD.
Vậy góc BAD = góc BCD = x độ.
Vì tứ giác ABCD là tứ giác lồi, tổng các góc trong tứ giác ABCD là 360 độ.
Ta có: góc A + góc B + góc C + góc D = 360 độ.
Vì góc D = 60 độ, góc A = 120 độ và góc B = 48 độ, ta có:
120 + 48 + góc C + 60 = 360
góc C = 360 - 120 - 48 - 60 = 132 độ.
Vậy số đo góc B là 48 độ và số đo góc C là 132 độ.
* Ib = bài 4
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có BC bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12.Tính độ dài các cạnh góc vuông AB và AC?
Cho tứ giác ABCD có A=700,B=1000,các tia phân giác của góc C và D cắt nhau tại O.Tính số đo COD
giúp mình với mình đang cần gấp ạ
a: Đặt \(\dfrac{AB}{5}=\dfrac{AC}{12}=k\)
=>AB=5k; AC=12k
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(25k^2+144k^2=26^2\)
=>\(k^2=4\)
=>k=2
=>AB=10cm; AC=24cm
b: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(\widehat{BCD}+\widehat{ADC}=360^0-70^0=290^0\)
=>\(2\cdot\left(\widehat{ODC}+\widehat{OCD}\right)=290^0\)
=>\(\widehat{OCD}+\widehat{ODC}=145^0\)
Xét ΔOCD có \(\widehat{COD}+\widehat{OCD}+\widehat{ODC}=180^0\)
=>\(\widehat{COD}=180^0-145^0=35^0\)
Đúng 1
Bình luận (0)
Cho tứ giác ABCD có
∠
A
75
o
;
∠
B
85
o
;
các tia phân giác của các góc ∠C và ∠D cắt nhau tại I. Số đo góc ∠CID là: A.
60
°
B.
70
°
C.
80
°
D.
90
°
Đọc tiếp
Cho tứ giác ABCD có ∠ A = 75 o ; ∠ B = 85 o ; các tia phân giác của các góc ∠C và ∠D cắt nhau tại I. Số đo góc ∠CID là:
A. 60 °
B. 70 °
C. 80 °
D. 90 °
1. Cho tứ giác ABCD, có hiệu của góc A và góc B là 400. Các tia phân giác của góc C và D cắt nhau tại H sao cho góc CHD có số đo là 1100. Chứng minh rằng AB vuông góc với BC.
2. Cho tứ giác ABCD có tổng của góc A và góc B là 2200. Các tia phân giác góc ngoài tại đỉnh C và D cắt nhau tại K. Tính số đo của góc CKD.
1:
Xét ΔCHD có \(\widehat{CHD}+\widehat{HCD}+\widehat{HDC}=180^0\)
=>\(\widehat{HCD}+\widehat{HDC}=180^0-110^0=70^0\)
=>\(\dfrac{1}{2}\left(\widehat{ADC}+\widehat{BCD}\right)=70^0\)
=>\(\widehat{ADC}+\widehat{BCD}=140^0\)
Xét tứ giác ABCD có
\(\widehat{ADC}+\widehat{BCD}+\widehat{DAB}+\widehat{ABC}=360^0\)
=>\(\widehat{DAB}+\widehat{ABC}=220^0\)
mà \(\widehat{DAB}-\widehat{ABC}=40^0\)
nên \(\widehat{ABC}=\dfrac{220^0-40^0}{2}=90^0\)
=>BA\(\perp\)BC
2:
Xét tứ giác ABCD có
\(\widehat{BAD}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(\widehat{BCD}+\widehat{ADC}=360^0-220^0=140^0\)
=>\(2\cdot\left(\widehat{KCD}+\widehat{KDC}\right)=140^0\)
=>\(\widehat{KCD}+\widehat{KDC}=70^0\)
Xét ΔCKD có
\(\widehat{CKD}+\widehat{KCD}+\widehat{KDC}=180^0\)
=>\(\widehat{CKD}=180^0-70^0=110^0\)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có các tia phân giác của góc A và D vuông góc với nhau tại Ea) Tứ giác ABCD là hình gì? Chứng minhb) Các tia phân giác của các góc B và C cắt nhau tại F. Các tia phân giác của các góc ngoài đỉnh A và D cắt nhau tại M. Các tia phân giác của các góc ngoài đỉnh B và C cắt nhau tại N. Chứng minh 4 điểm M,N,E,F thẳng hàngc) Cho biết AB a, BC b, CD c, DA d (a,b,c,d có cùng đơn vị độ dài). CMR: Nếu a+cb+d thì E trùng với FGiúp em với ạ, vẽ hình giúp em nhé. Cảm ơn mn ạ
Đọc tiếp
Cho tứ giác ABCD có các tia phân giác của góc A và D vuông góc với nhau tại E
a) Tứ giác ABCD là hình gì? Chứng minh
b) Các tia phân giác của các góc B và C cắt nhau tại F. Các tia phân giác của các góc ngoài đỉnh A và D cắt nhau tại M. Các tia phân giác của các góc ngoài đỉnh B và C cắt nhau tại N. Chứng minh 4 điểm M,N,E,F thẳng hàng
c) Cho biết AB = a, BC = b, CD = c, DA= d (a,b,c,d có cùng đơn vị độ dài). CMR: Nếu a+c=b+d thì E trùng với F
Giúp em với ạ, vẽ hình giúp em nhé. Cảm ơn mn ạ