a: =64x^4+16x^2y^2+y^4-16x^2y^2

=(8x^2+y^2)^2-(4xy)^2

=(8x^2+y^2-4xy)(8x^2+y^2+4xy)

b: =x^8+2x^4+1-x^4

=(x^4+1)^2-x^4

=(x^4-x^2+1)(x^4+x^2+1)

=(x^4-x^2+1)(x^4+2x^2+1-x^2)

=(x^4-x^2+1)(x^2+1-x)(x^2+x+1)

c: =(x+1)(x^2-x+1)+2x(x+1)

=(x+1)(x^2-x+1+2x)

=(x+1)(x^2+x+1)

d: =(x^2-1)(x^2+1)-2x(x^2-1)

=(x^2-1)(x^2-2x+1)

=(x-1)^2*(x-1)(x+1)

=(x+1)(x-1)^3

a) \(4x\left(a-b\right)+6xy\left(b-a\right)\)

\(=4x\left(a-b\right)-6xy\left(a-b\right)\)

\(=\left(4x-6xy\right)\left(a-b\right)\)

\(=2x\left(2-3y\right)\left(a-b\right)\)

b) \(\left(6x+3\right)-\left(2x-5\right)\left(2x+1\right)\)

\(=3\left(2x+1\right)-\left(2x-5\right)\left(2x+1\right)\)

\(=\left(3-2x+5\right)\left(2x+1\right)\)

\(=\left(8-2x\right)\left(2x+1\right)\)

\(=2\left(4-x\right)\left(2x+1\right)\)

g: \(\left(3x-1\right)^2-\left(x+3\right)^2\)

\(=\left(3x-1-x-3\right)\left(3x-1+x+3\right)\)

\(=\left(2x-4\right)\left(4x+2\right)\)

\(=4\left(x-2\right)\left(2x+1\right)\)

\(a)\left(x^2+2x\right)\left(x^2+2x+4\right)+3\)

Để đơn giản hơn cũng như là dễ nhìn hơn thì ta :

Đặt : \(x^2+2x=a\)

Do đó ta có đa thức :

\(a.\left(a+4\right)+3=a^2+4a+3\)

\(=a^2+a+3a+3\)

\(=a\left(a+1\right)+3\left(a+1\right)\)

\(=\left(a+1\right)\left(a+3\right)\)

\(=\left(x^2+2x+1\right)\left(x^2+2x+3\right)\)

\(=\left(x+1\right)^2.\left(x^2+2x+3\right)\)

Hoặc bạn có thể đặt \(x^2+2x+2=t\)

Thì \(P=\left(x^2+2x\right)\left(x^2+2x+4\right)+3\)

\(P=\left(t-2\right)\left(t+2\right)+3\)

\(P=t^2-4+3\)

\(P=t^2-1\)

\(P=\left(t-1\right)\left(t+1\right)\)

\(P=\left(x^2+2x+1\right)\left(x^2+2x+3\right)\)

\(P=\left(x+1\right)^2\left(x^2+2x+3\right)\)

a) \(\left(x^2+2x\right).\left(x^2+2x+4\right)+3\)

\(=x^4+4x^3+4x^2+4x^3+16x^2+16x\)

\(=x^4+8x^3+20x^2+16x\)

\(=\left(x^4+8x^3+20x^2+16x\right)+3\)

\(=x^4+8x^3+20x^2+16x+3\)

\(x^6+2x^5+x^4-2x^3-2x^2+1=\left(x^3+x^2-1\right)^2\)

a)\(x^4-2x^3+2x-1=x^4-x^3-x^3+x+x-1\)

\(=x^3\left(x-1\right)-x\left(x^2-1\right)+\left(x-1\right)\)

\(=x^3\left(x-1\right)-x\left(x-1\right)\left(x+1\right)+\left(x-1\right)\)

\(=x^3\left(x-1\right)-\left(x^2+x\right)\left(x-1\right)+\left(x-1\right)\)

\(=\left(x-1\right)\left[x^3-\left(x^2+x\right)+1\right]\)

\(=\left(x-1\right)\left(x^3-x^2-x+1\right)\)

\(=\left(x-1\right)\left[x^2\left(x-1\right)-\left(x-1\right)\right]\)

\(=\left(x-1\right)\left(x-1\right)\left(x^2-1\right)\)

\(=\left(x-1\right)\left(x-1\right)\left(x-1\right)\left(x+1\right)\)

\(=\left(x-1\right)^3\left(x+1\right)\)

b)\(x^4+2x^3+2x^2+2x+1=x^4+x^3+x^3+x^2+x^2+x+x+1\)

\(=x^3\left(x+1\right)+x^2\left(x+1\right)+x\left(x+1\right)+\left(x+1\right)\)

\(=\left(x+1\right)\left(x^3+x^2+x+1\right)\)

\(=\left(x+1\right)\left[x^2\left(x+1\right)+\left(x+1\right)\right]\)

\(=\left(x+1\right)\left(x+1\right)\left(x^2+1\right)\)

\(=\left(x+1\right)^2\left(x^2+1\right)\)

a) =

\(x^4-x^3-x^3+x^2-x^2+x+x-1=x^3\left(x-1\right)-x^2\left(x-1\right)-x\left(x-1\right)+\left(x-1\right)=\left(x-1\right)\left(x^3-x^2-x+1\right)\)

cái vế x³-x²-x+1 tự phân tích nhá

nghiệm = 1 và -1 

a: \(x^8+x^4+1\)

\(=x^8+2x^4+1-x^4\)

\(=\left(x^4+1\right)^2-x^4\)

\(=\left(x^4+1+x^2\right)\left(x^4+1-x^2\right)\)

\(=\left(x^4+2x^2+1-x^2\right)\left(x^4-x^2+1\right)\)

\(=\left(x^4-x^2+1\right)\cdot\left[\left(x^2+1\right)^2-x^2\right]\)

\(=\left(x^4-x^2+1\right)\left(x^2+1-x\right)\left(x^2+1+x\right)\)

b: \(\left(x^2+1\right)^2+3x\left(x^2+1\right)+2x^2\)

\(=\left(x^2+1\right)^2+x\left(x^2+1\right)+2x\left(x^2+1\right)+2x^2\)

\(=\left(x^2+1\right)\left(x^2+x+1\right)+2x\left(x^2+1+x\right)\)

\(=\left(x^2+x+1\right)\left(x^2+2x+1\right)\)

\(=\left(x^2+x+1\right)\left(x+1\right)^2\)

a) \(x^4-2x^3+2x-1\)

\(=x^4-x^3-x^3+2x-2+1\)

\(=\left(x^4-x^3\right)+\left(2x-2\right)-\left(x^3-1\right)\)

\(=x^3\left(x-1\right)+2\left(x-1\right)-\left(x-1\right)\left(x^2+x+1\right)\)

\(=\left(x-1\right)\left(x^3+2-x^2-x-1\right)\)

\(=\left(x-1\right)\left(x^3-x^2-x+1\right)\)

\(=\left(x-1\right)\left[\left(x^3-x^2\right)-\left(x-1\right)\right]\)

\(=\left(x-1\right)\left[x^2\left(x-1\right)-\left(x-1\right)\right]\)

\(=\left(x-1\right)\left(x^2-1\right)\left(x-1\right)\)

\(=\left(x-1\right)^2\left(x-1\right)\left(x+1\right)\)

\(=\left(x-1\right)^3\left(x+1\right)\)

b) \(x^4+2x^3+2x^2+2x+1\)

\(=\left(x^4+2x^2+1\right)+\left(2x^3+2x\right)\)

\(=\left(x^2+1\right)^2+2x\left(x^2+1\right)\)

\(=\left(x^2+1\right)\left(x^2+1+2x\right)\)

\(=\left(x^2+1\right)\left(x+1\right)^2\)

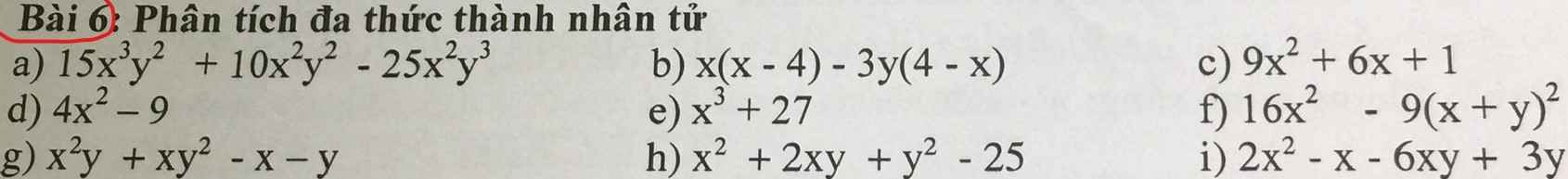
Bài 6:

c: \(9x^2+6x+1=\left(3x+1\right)^2\)

d: \(4x^2-9=\left(2x-3\right)\left(2x+3\right)\)

e: \(x^3+27=\left(x+3\right)\left(x^2-3x+9\right)\)

a: \(x^4-2x^3+x^2-2x\)

\(=\left(x^4-2x^3\right)+\left(x^2-2x\right)\)

\(=x^3\left(x-2\right)+x\left(x-2\right)\)

\(=x\left(x-2\right)\left(x^2+1\right)\)

b: \(x^4+x^3-8x-8\)

\(=\left(x^4+x^3\right)-\left(8x+8\right)\)

\(=x^3\left(x+1\right)-8\left(x+1\right)\)

\(=\left(x+1\right)\left(x^3-8\right)\)

\(=\left(x+1\right)\left(x-2\right)\left(x^2+2x+4\right)\)