Ai giúp mik câu 28,29 với

Những câu hỏi liên quan
sách VNEN lớp 7 bài 3 trang 28,29
bài 1,2,3.giúp mik
ai giúp mik câu 4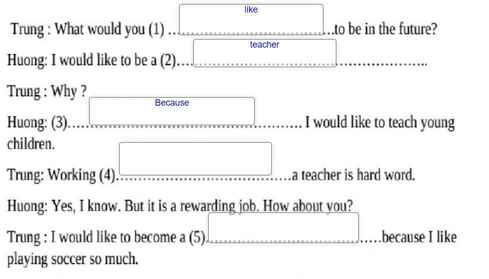
ai giúp mik câu 4 với ạ?
ai giả giúp mik câu 6 và câu 7 với 
Ai giúp mik 2 câu này với mik đang gấp. Cảm ơn ạ!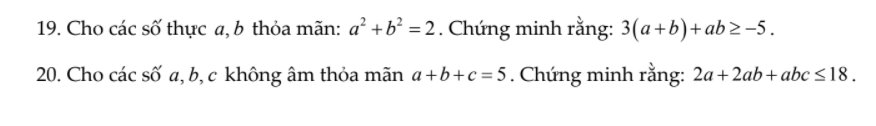
19.
\(\left(a+b\right)^2\le2\left(a^2+b^2\right)=4\Rightarrow-2\le a+b\le2\)
\(P=3\left(a+b\right)+ab=3\left(a+b\right)+\dfrac{\left(a+b\right)^2-\left(a^2+b^2\right)}{2}=\dfrac{1}{2}\left(a+b\right)^2+3\left(a+b\right)-1\)
Đặt \(a+b=x\Rightarrow-2\le x\le2\)
\(P=\dfrac{1}{2}x^2+3x-1=\dfrac{1}{2}\left(x+2\right)\left(x+4\right)-5\ge-5\) (đpcm)
Dấu "=" xảy ra khi \(x=-2\) hay \(a=b=-1\)
Đúng 1
Bình luận (0)
20.
Đặt \(P=2a+2ab+abc\)
\(P=2a+ab\left(2+c\right)\le2a+\dfrac{a}{4}\left(b+2+c\right)^2=2a+\dfrac{a}{4}\left(7-a\right)^2\)
\(P\le\dfrac{1}{4}\left(a^3-14a^2+57a-72\right)+18=18-\dfrac{1}{4}\left(8-a\right)\left(a-3\right)^2\le18\) (đpcm)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(3;2;0\right)\)
Đúng 1
Bình luận (0)
ai giải giúp mik câu c với 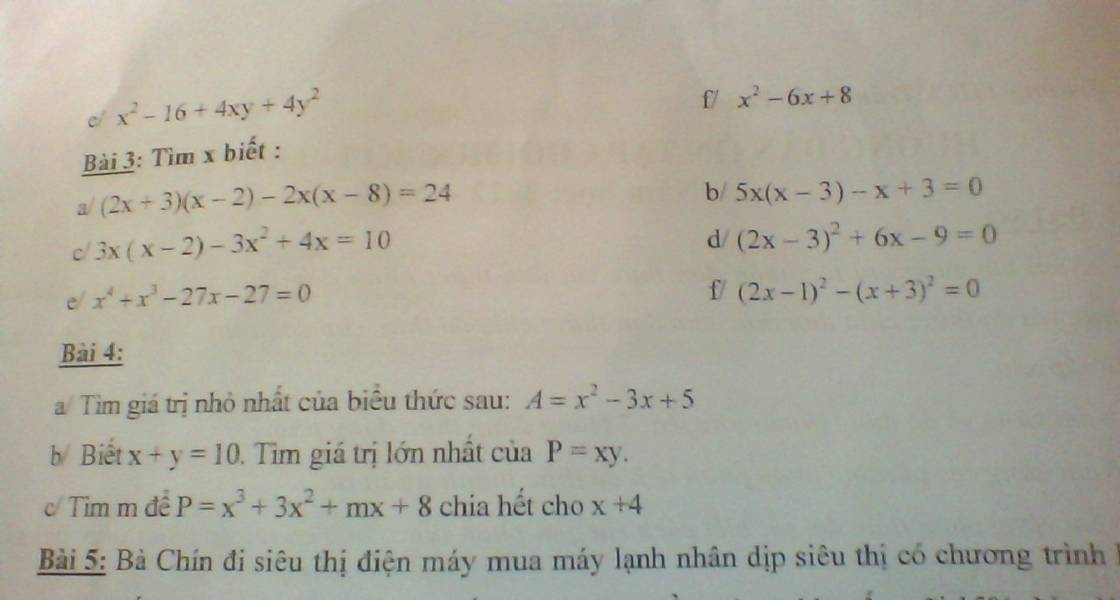
Bài 4. c)
\(P\left(x\right)=x^3+3x^2+mx+8\) chia hết cho \(x+4\) suy ra \(P\left(-4\right)=0\)
khi đó \(\left(-4\right)^3+3.\left(-4\right)^2+m.\left(-4\right)+8=0\Leftrightarrow m=-2\).
Đúng 1
Bình luận (0)
ai giải giúp mik câu 5 với
$a) n_{Fe_2O_3} = \dfrac{32}{160} = 0,2(mol)$
$b) m_{O_2} = 0,12.32 = 3,84(gam)$
$c) n_{CuSO_4} = \dfrac{1,2.6^{23}}{6.10^{23}} = 0,2(mol)$
$m_{hh} = 0,12.342 + 0,2.160 = 73,04(GAM)$
$d) n_{CO_2} = \dfrac{3,6.10^{23}}{6.10^{23}} = 0,6(mol)$
$V_{CO_2} = 0,6.22,4 = 13,44(lít)$
$e) n_{CO_2} = 0,5(mol) \Rightarrow V_{hh} = (0,5 + 0,5).22,4 = 22,4(lít)$
Đúng 1
Bình luận (0)
ai giải giúp mik câu 4 với 
$a) Zn + 2HCl \to ZnCl_2 + H_2$
$b)n_{Zn} = \dfrac{1,2.10^{23}}{6.10^{23}} = 0,2(mol) ; n_{H_2} = \dfrac{4,48}{22,4} = 0,2(mol)$
Bảo toàn khối lượng : $m_{Zn} + m_{HCl} = m_{ZnCl_2} + m_{H_2}$
$\Rightarrow m = 0,2.65 + 0,4.36,5 - 0,2.2 = 27,2(gam)$
Đúng 1
Bình luận (0)
ai giúp mik câu c với ạ

-Lưu ý: Chỉ mang tính chất tóm tắt lại bài làm, bạn không nên trình bày theo!
c/ △ABC có: BD, CE là các đường cao và BD, CE cắt nhau tại H.
\(\Rightarrow\)AH là đường cao mà AH cắt BC tại Q \(\Rightarrow\)AH⊥BC tại Q.
△BEC∼△BQA (g-g) \(\Rightarrow\dfrac{BE}{BQ}=\dfrac{BC}{BA}\Rightarrow\dfrac{BE}{BC}=\dfrac{BQ}{BA}\)
\(\Rightarrow\)△BEQ∼△BCA (c-g-c) \(\Rightarrow\)\(\widehat{BQE}=\widehat{BAC}\) (1)
△BDC∼△AQC (g-g) \(\Rightarrow\dfrac{BC}{AC}=\dfrac{DC}{QC}\Rightarrow\dfrac{BC}{DC}=\dfrac{AC}{QC}\)
\(\Rightarrow\)△DQC∼△BCA (c-g-c) \(\Rightarrow\)\(\widehat{DQC}=\widehat{BAC}\) (2)
-Từ (1) và (2) suy ra: \(\widehat{BQE}=\widehat{DQC}\Rightarrow\widehat{AQE}=\widehat{AQD}\)
\(\Rightarrow\)QA là tia p/g của góc EQD
Đúng 1
Bình luận (0)
ai giải giúp mik câu này với





















