Gọi đường tròn (O) đi qua ba điểm A, B, C. Đường phân giác của  cắt cung nhỏ AC tại E. Xét hai tam giác ABE và DBC, chúng có:  (gt),  (hai góc nội tiếp cùng chắn cung AB).

Vậy ∆ ABE ~ ∆ DBC =>  = 

=> AB.BC = BD.BE = (BD + DE).BD = BD2 + DE.BD

=> BD2 = AB.BC - DE.BD (1)

Dễ dàng có ∆ DBC ~ ∆ DAE =>  =  => DE.BD = AD.DC (2).

Thay (2) vài (1) ta có điều phải chứng minh.

Từ A dựng đường thẳng //với BC cắt BD kéo dài tại E

\(\Rightarrow\widehat{E_1}=\widehat{B_2}\) (góc so le trong)

Mà \(\widehat{B_1}=\widehat{B_2}\)

\(\Rightarrow\widehat{B_1}=\widehat{E_1}\) => tg ABE cân tại A => BA=AE (1)

Áp dụng hệ quả định lý ta let đối với tam giác ta có

\(\frac{CD}{DA}=\frac{BC}{AE}\) (2)

Từ (1) và (2) \(\Rightarrow\frac{CD}{DA}=\frac{BC}{BA}=\frac{2BA}{BA}=2\Rightarrow CD=2DA\)

Xét ΔBAC có BD là phân giác

nên DA/DC=BA/BC=1/2

=>DC=2DA

a: Xét ΔBDE và ΔBCE có

BD=BC

\(\widehat{DBE}=\widehat{CBE}\)

BE chung

Do đó: ΔBDE=ΔBCE

b: Ta có: ΔBDE=ΔBCE

=>ED=EC

=>E nằm trên đường trung trực của DC(1)

Ta có: BD=BC

=>B nằm trên đường trung trực của CD(2)

Ta có: KD=KC

=>K nằm trên đường trung trực của CD(3)

Từ (1),(2),(3) suy ra B,E,K thẳng hàng

=>B,E,K cùng nằm trên đường trung trực của DC

=>EK\(\perp\)DC

c: ΔAHD vuông tại H có \(\widehat{DAH}=45^0\)

nên ΔAHD vuông cân tại H

Xét ΔBDC có BD=BC

nên ΔBCD cân tại B

mà \(\widehat{BDC}=45^0\)

nên ΔBCD vuông cân tại B

=>\(\widehat{ABC}=90^0\)

Dễ thế mà k bt lm . Google đi

Cho tam giác ABC có BC = 2BA . BD là phân giác của tam giác ABC . Chứng minh DC = 2DA

chứng minh à bạn

A)XÉT \(\Delta ABD\)VÀ\(\Delta HBD\)CÓ

\(\widehat{BAD}=\widehat{BHD}=90^o\)

\(\widehat{ABD}=\widehat{DBH}\left(GT\right)\)

BD LÀ CẠNH CHUNG

=>\(\Delta ABD\)=\(\Delta HBD\)(CẠNH HUYỀN - GÓC NHỌN ) ( ĐPCM)

GỌI I LÀ GIAO ĐIỂM CỦA BD VÀ AH

XÉT \(\Delta ABI\)VÀ\(\Delta HBI\)CÓ

\(AB=BH\left(\Delta ABD=\Delta HBD\right)\)

\(\widehat{ABD}=\widehat{DBH}\left(GT\right)\)

BI LÀ CẠNH CHUNG

=>\(\Delta ABI\)=\(\Delta HBI\)(C-G-C)

\(\Rightarrow\widehat{AIB}=\widehat{HIB}\)( HAI GÓC TƯƠNG ỨNG)

MÀ HAI GÓC NÀY KỀ BÙ 

\(\Rightarrow\widehat{AIB}=\widehat{HIB}=\frac{180^o}{2}=90^o\left(1\right)\)

mà\(\Delta ABI\)=\(\Delta HBI\)(C-G-C)

=> AI=HI( HAI CẠNH TƯƠNG ỨNG ) (2)

TỪ 1 VÀ 2 => BI LÀ ĐƯỜNG TRUNG TRỰC CỦA AH HAY BD LÀ ĐƯỜNG TRUNG TRỰC CỦA AH(ĐPCM)

B)

b)  

Vì  \(\Delta\)DBA =\(\Delta\) DBH ( cm ở câu a )

=) AD = DH 

Xét\(\Delta\)DHC ( DHC = 90 ) có :

DC là cạnh huyền 

\(\Rightarrow\) DC là cạnh lớn nhất 

\(\Rightarrow DC>DH\)

mà DH = AD

\(\Rightarrow AD< DC\)

a, Xét △ABD vuông tại A và △HBD vuông tại H

Có: BD là cạnh chung

       ABD = HBD (gt)

=> △ABD = △HBD (ch-gn)

=> AB = BH (2 cạnh tương ứng) => B thuộc đường trung trực của AH

và AD = HD (2 cạnh tương ứng) => D thuộc đường trung trực của AH

=> BD là đường trung trực của AH

b, Xét △HDC vuông tại H có: DC > DH (quan hệ giữa đường xiên và đường vuông góc)

=> DC > AD

a) Xét \(\Delta ABD\)và \(\Delta HBD\)có :

                  \(\widehat{BAD}=\widehat{AHD}\left(=90^o\right)\)

                \(BD\)chung

                  \(\widehat{B_1}=\widehat{B_2}\left(gt\right)\)

\(\Rightarrow\Delta ABD=\Delta HBD\left(ch-gn\right)\)

\(\Rightarrow AB=BH\)( 2 cạnh tương ứng ) \(\Rightarrow\)B thuộc đường trung trực của AH \(\left(1\right)\)

và \(AD=HD\)( 2 cạnh tương ứng ) \(\Rightarrow\)D thuộc đường trung trực của AH \(\left(2\right)\)

Từ \(\left(1\right);\left(2\right)\Rightarrow\)BD là trung trực của AH

b) Xét \(\Delta DHC\)vuông tại H , ta có :

      \(DH< DC\left(cgv< ch\right)\)

mà \(AD=HD\left(cmt\right)\)

\(\Rightarrow AD< DC\)

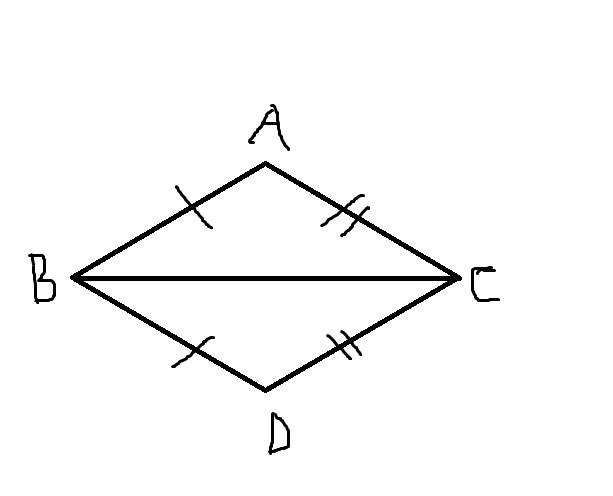
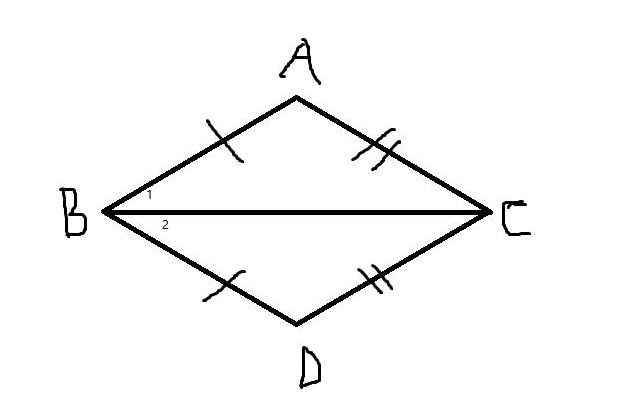
a) Xét ΔABC và ΔDBC có:
       AB=BC (gt)
        BC chung
      ∠B1 = ∠B2
 ⇒ ΔABC = ΔDBC (c-g-c)

b) Từ kết quả câu a, ta có: ΔABC = ΔDBC
                   ⇒ AC = DC (2 cạnh tương ứng)