cho (d): y=(m -1)x-m
(d1): y= (2m+1)x+m2 +1
a) c/m (d) luôn đi qua 1 điểm cố định
b) c/m (d1) ko đi qua điểm cố định
Cho 2 đường thẳng ( d1) : y = ( m - 1 )x - m
( d2 ) : y = ( 2m + 1 )x + m2 + 1
a ) Chứng tỏ (d1) đi qua 1 điểm cố định
b ) Cmr ( d2 ) không đi qua điểm cố định đó
c ) Cmr với mọi giá trị m hai đường thẳng (d1) và (d2) không thể trùng nhau
d ) Tìm giá trị của m để ( d1 ) song song ( d2 ), ( d1 ) cắt ( d2 )
Cho (d1) y= 4mx - ( m + 5 ) ; (d2) y= ( 3m^2 + 1)x + m^2 - 4
a) tìm m để đồ thị (d1) đi qua M(2;3)
b. CM khi m thay đổi thì d1 luôn đi qua điểm A cố định d2 đi qua B cố định
c. khoảng cách AB = ???
d. Tìm m để d1 // d2
e. Tìm m để d1 cắt d2 . tìm giao điểm khi m=2
a/
\(\Rightarrow3=4m.2-m-5\Leftrightarrow m=\dfrac{8}{5}\)
b/
Tọa độ A là \(A\left(x_0;y_0\right)\)
\(\Rightarrow y_0=4mx_0-m-5\forall m\)
\(\Leftrightarrow\left(4x_0-1\right)m-\left(y_0+5\right)=0\forall m\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x_0-1=0\\y_0+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\dfrac{1}{4}\\y_0=-5\end{matrix}\right.\)
=> d1 luân đi qua điểm A cố định \(A\left(\dfrac{1}{4};-5\right)\forall m\)
Tọa độ B là \(B\left(x_1;y_1\right)\)
\(\Rightarrow y_1=\left(3m^2+1\right)x_1+m^2-4\forall m\)
\(\Leftrightarrow3m^2x_1+x_1+m^2-4-y_1=0\forall m\)
\(\Leftrightarrow\left(3x_1+1\right)m^2+x_1-y_1-4=0\forall m\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x_1+1=0\\x_1-y_1-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{3}\\y_1=-\dfrac{13}{3}\end{matrix}\right.\)
=> d2 luân đi qua điểm B cố định \(B\left(-\dfrac{1}{3};-\dfrac{13}{3}\right)\)
d/ d1//d2 khi
\(\left\{{}\begin{matrix}4m=3m^2+1\\-m-5\ne m^2-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m_1=1\\m_2=\dfrac{1}{3}\end{matrix}\right.\\m^2+m+1\ne0\end{matrix}\right.\)
Ta có \(m^2+m+1>0\forall m\)
\(\Rightarrow\left[{}\begin{matrix}m_1=1\\m_2=\dfrac{1}{3}\end{matrix}\right.\)
e/
\(\Rightarrow4mx-\left(m+5\right)=\left(3m^2+1\right)x+m^2-4\) tìm m để phương trình có nghiệm
Tìm giao
\(\Rightarrow4mx-\left(m+5\right)=\left(3m^2+1\right)x+m^2-4\) khi m=2
Thay m=2 tìm x rồi thay vào d1 hoặc d2 để tìm y
Cho đường thẳng d 1 :y = mx + 2m - 1 (với m là tham số) và d 2 : y = x + 1
c) Chứng mình rằng đường thẳng d 1 luôn đi qua một điểm cố định với mọi giá trị của m.
c) Giả sử đường thẳng d 1 luôn đi qua một điểm cố định ( x 1 ; y 1 ) với mọi giá trị của m.
⇒ y 1 = m x 1 + 2m - 1 với mọi m
⇔ m( x 1 + 2) - 1 - y 1 = 0 với mọi m
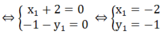
Vậy điểm cố định mà d 1 luôn đi qua với mọi giá trị của m là (-2; -1).
Cho đường thẳng d:y=(m-2)x+2+m với m là tham số
a.tìm m để d cắt (d1):y=2x-2m+1 tại một điểm trên trục tung
b. tìm m để d cùng các đường thẳng d1:y=x+2 và d2:y=4-3x đồng quy
c. chứng minh d luôn đi qua 1 điểm cố định với mọi m
a: Để (d) cắt (d1) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}m-2\ne2\\-2m+1=m+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne4\\-3m=1\end{matrix}\right.\Leftrightarrow m=-\dfrac{1}{3}\)
b: Tọa độ giao điểm của d1 và d2 là:
\(\left\{{}\begin{matrix}x+2=4-3x\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x=2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}+2=\dfrac{5}{2}\end{matrix}\right.\)
Thay x=1/2 và y=5/2 vào (d), ta được:
\(\dfrac{1}{2}\left(m-2\right)+2+m=\dfrac{5}{2}\)
=>\(\dfrac{1}{2}m-1+m+2=\dfrac{5}{2}\)
=>\(\dfrac{3}{2}m=\dfrac{3}{2}\)
=>m=1
c: (d): y=(m-2)x+m+2
=mx-2x+m+2
=m(x+1)-2x+2
Tọa độ điểm cố định mà (d) luôn đi qua là:
\(\left\{{}\begin{matrix}x+1=0\\y=-2x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\cdot\left(-1\right)+2=4\end{matrix}\right.\)
cho đường thẳng d y = (m + 2) x + m Tìm m để d
a, song song với đường thẳng d1 : y = -2 x + 3
b ,vuông góc với đường thẳng d2 : y = 1 / 3 x + 1
C, đi qua điểm N( 1,3)
D, Tìm điểm cố định Mà D luôn đi qua với mọi m
\(a,d//d_1\Leftrightarrow\left\{{}\begin{matrix}m+2=-2\\m\ne3\end{matrix}\right.\Leftrightarrow m=-4\\ b,d\perp d_2\Leftrightarrow\dfrac{1}{3}\left(m+2\right)=-1\Leftrightarrow m+2=-3\Leftrightarrow m=-5\\ c,d.qua.N\left(1;3\right)\Leftrightarrow x=1;y=3\Leftrightarrow3=m+2+m\\ \Leftrightarrow2m=1\Leftrightarrow m=\dfrac{1}{2}\)
\(d,\) Gọi điểm đó là \(A\left(x_1;y_1\right)\)
\(\Leftrightarrow y_1=\left(m+2\right)x_1+m\\ \Leftrightarrow y_1-mx_1-2x_1-m=0\\ \Leftrightarrow-m\left(x_1+1\right)+y_1-2x_1=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_1+1=0\\y_1-2x_1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-1\\y_1=-2\end{matrix}\right.\)
Vậy \(A\left(-1;-2\right)\) luôn đi qua D với mọi m
Cho đường thẳng d1: y = (2m – 1)x + 3m – 2 (m là tham số)
d2 : y = (n – 2)x + 3 (n là tham số)
Tìm n biết d1 và d2 cắt nhau tại điểm J là điểm cố định mà d1 luôn đi qua với mọi m.
Cho (d1) y= 4mx - ( m + 5 ) ; (d2) y= ( 3m^2 + 1)x + m^2 - 4
a) tìm m để đồ thị (d1) đi qua M(2;3)
b. CM khi m thay đổi thì d1 luôn đi qua điểm A cố định d2 đi qua B cố định
c. khoảng cách AB = ???
d. Tìm m để d1 // d2
e. Tìm m để d1 cắt d2 . tìm giao điểm khi m=2
1 . Cho hai đường thẳng (d1):mx+(m-2)y+m+2=0 và (d2):(2-m)x+my-m-2=0
a) Tìm điểm cố định mà (d1) luôn đi qua và điểm cố định mà (d2) luôn đi qua
b) Chứng minh hai đường thẳng (d1) ,(d2) luôn cắt nhau tại một điểm I và khi m thay
đổi thì điểm I luôn thuộc một đường tròn cố định.
2 . Cho các số thực a, b, c, d thỏa mãn a > 1, b > 1, c > 1, d > 1. Chứng minh
\(\frac{a^2}{b-1}+\frac{b^2}{c-1}+\frac{c^2}{a-1}\ge16\)
EM CẦN GẤP Ạ..GIÚP EM VỚI Ạ..
1)Cho hàm số y=(m-1)x+m (d)
a)Tìm m để khoảng cách từ gốc tọa độ đến (d) bằng 1
b)Chứng minh (d) luôn đi qua 1 điểm cố định với mọi m
2)Cho 3 đường thẳng d1:y=x-2;d2:y=2-x;d3:y=(2-m)x+1.Tính góc tạo bởi đường thẳng d1 và trục Ox