P = (10.102.103.104. ….. . 109):(105.1010.1025) ai giúp mình bài này với mình đang cần gấp,làm ơn.Mình cảm ơn.

Những câu hỏi liên quan
Bài 1:Tính giá trị của biểu thức: a, P = ( 10.102.103.104...109) : ( 105.1010.1025); b, Q = ( 29.3 + 29.5) : 212 Nhanh nha mn
b) Ta có: \(Q=\dfrac{\left(29\cdot3+29\cdot5\right)}{212}\)
\(=\dfrac{29\cdot\left(3+5\right)}{212}\)
\(=\dfrac{29\cdot8}{212}=\dfrac{58}{53}\)
Đúng 0
Bình luận (0)
Ai Giải giúp mình 2 bài này với ạ
Mình đang cần gấp, xin cảm ơn.
Bài 3:
a. \(R=R1+R2=15+30=45\Omega\)
b. \(\left\{{}\begin{matrix}I=U:R=9:45=0,2A\\I=I1=I2=0,2A\left(R1ntR2\right)\end{matrix}\right.\)
c. \(\left\{{}\begin{matrix}U1=R1.I1=15.0,2=3V\\U2=R2.I2=30.0,2=6V\end{matrix}\right.\)
Bài 4:
\(I1=U1:R1=6:3=2A\)
\(\Rightarrow I=I1=I2=2A\left(R1ntR2\right)\)
\(U=R.I=\left(3+15\right).2=36V\)
\(U2=R2.I2=15.2=30V\)
Đúng 1
Bình luận (0)
Ai giúp mình 2 cái bài này với ! Mình đang cần gấp , mình cảm ơn trc nha 😊✌️
Ai giúp mình làm 3 câu này với ạ mình đang cần gấp. Cảm ơn mn nhiều ạ.
Mnguoi ơi giúp mình làm bài này với ạ. Mình đang cần gấp. Cảm ơn mọi người nhiều lắm ạ❤
1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Đúng 0
Bình luận (0)
Trời ơi ! Ai cứu mình với , giúp mình 2 cái bài này đc ko ? Mình đang cần gấp ạ ! Cảm ơn trc nhen 😊
Trời trời giúp mình với mấy thần đồng tiếng anh ơi , mình sắp toang ròi 😢😢😢
Đúng 0
Bình luận (1)
Các bạn giúp mình làm bài này nhé mình đang cần gấp cảm ơn các bạn nhìu...
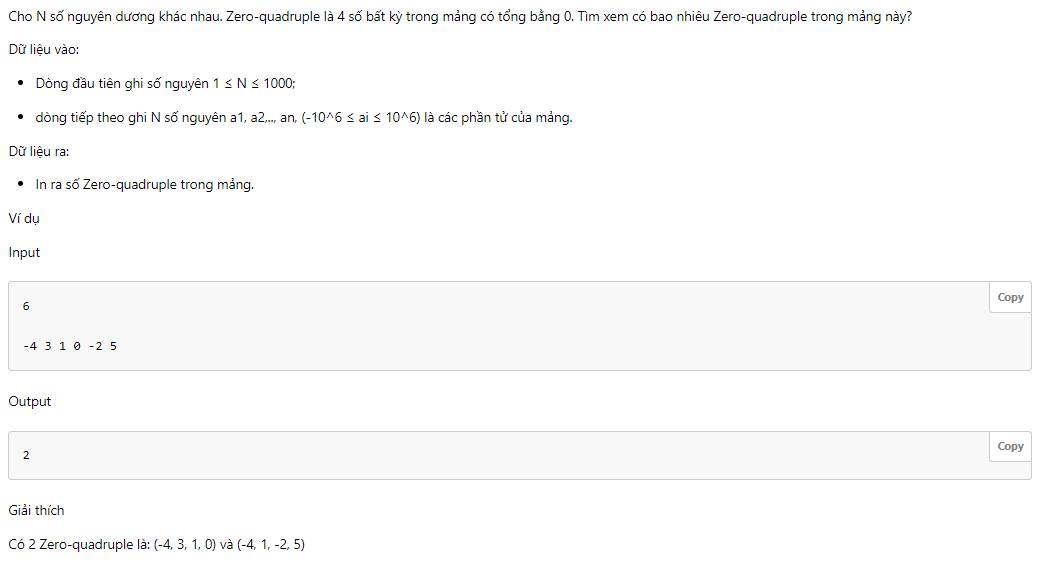 Bạn nào biết làm bài này ko làm giúp mình với mình đang cần bài này ạ! Xin cảm ơn
Bạn nào biết làm bài này ko làm giúp mình với mình đang cần bài này ạ! Xin cảm ơn
giúp mình giải bài này với ạ, mình đang cần gấp, mình 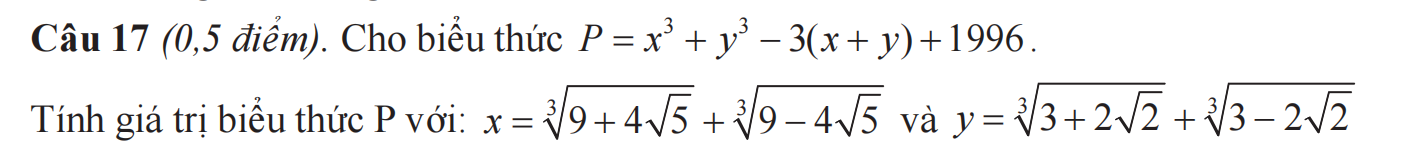 cảm ơn
cảm ơn
\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt[]{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(=18+3\sqrt{81-80}.x=18+3x\)\(\Rightarrow x^3-3x=18\left(1\right)\)
\(y=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(\Rightarrow y^3=3+2\sqrt{2}+3-2\sqrt{2}+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}.y=6+3y\)\(\Rightarrow y^3-3y=6\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow P=x^3+y^3-3\left(x+y\right)+1996=x^3-3x+y^3-3y+1996\)
\(=18+6+1996=2020\)
Đúng 1
Bình luận (0)



















