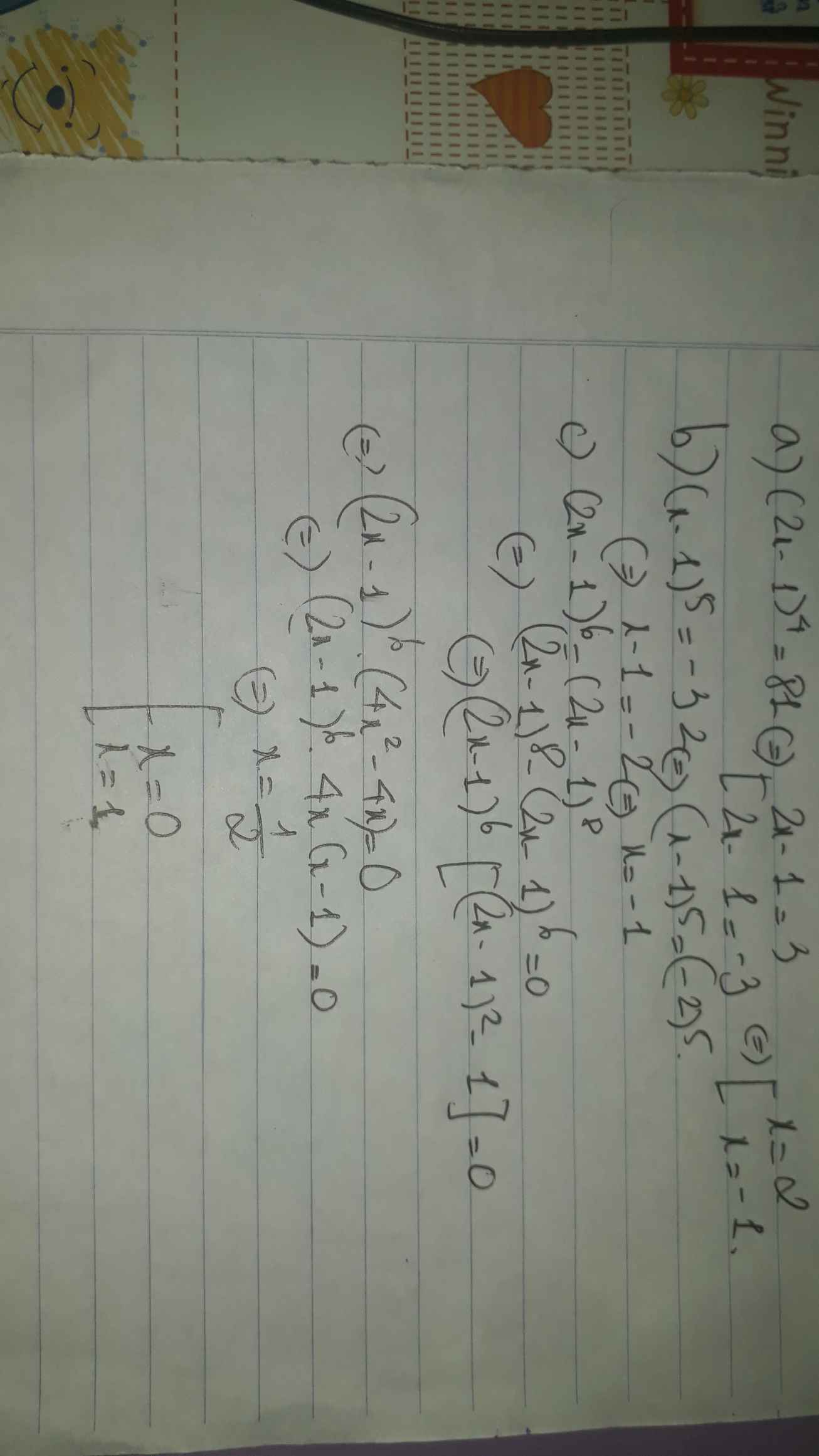Tìm số hữu tỉ x , biết:
4.(2x+1)2=576

Những câu hỏi liên quan
Tìm 2 số hữu tỉ a sao cho x < a < y, biết rằng:
a) x = 21,3678... và y = 21, 576...
b) x = -25,4832... và y = -24,9736...
Bài 1: Tìm số hữu tỉ x biết:a, ( 2x - 1 )4 81 b, ( x - 1 )5 -32 c, ( 2x - 1 )6 ( 2x - 1 )8Bài 2: Tìm các số tự nhiên x, y biết rằng: a, 2x + 1 . 3y 12x. b, 10x : 5y 20y c, 2x 4y - 1 và 27y 3x + 8
Đọc tiếp
Bài 1: Tìm số hữu tỉ x biết:
a, ( 2x - 1 )4 = 81 b, ( x - 1 )5 = -32
c, ( 2x - 1 )6 = ( 2x - 1 )8
Bài 2: Tìm các số tự nhiên x, y biết rằng:
a, 2x + 1 . 3y = 12x. b, 10x : 5y = 20y
c, 2x = 4y - 1 và 27y = 3x + 8
Bài 2:
a: Ta có: \(2^{x+1}\cdot3^y=12^x\)
\(\Leftrightarrow2^{x+1}\cdot3^y=2^{2x}\cdot3^x\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1=2x\\x=y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm số hữu tỉ x, biết rằng:
(2x-1)^6 =(2x-1)^8
Các giá trị x thu được là \(0,1,\frac{1}{2}\)
Đúng 0
Bình luận (0)
\(\left(2x-1\right)^6=\left(2x-1\right)^8\)
\(\Leftrightarrow\left(2x-1\right)^6-\left(2x-1\right)^8=0\)
\(\Leftrightarrow\left(2x-1\right)^6.[1-\left(2x-1\right)^2]=0\)
\(\Leftrightarrow\orbr{\begin{cases}\left(2x-1\right)^6=0\\1-\left(2x-1\right)^2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}2x-1=0\\\left(2x-1\right)^2=1\end{cases}}\)
Còn bn tự giải nhé
Xem thêm câu trả lời
1 tìm các số hữu tỉ x,y thỏa mãn 3x2y và x+y-152 tìm các số hữu tỉ x,y biết rằng a) x+y-z20 và dfrac{x}{4}dfrac{y}{3}dfrac{z}{5}b)dfrac{x}{11}dfrac{y}{12};dfrac{y}{3}dfrac{z}{7} và 2x-y+z1523) chia số 552 thành ba phần tỉ lệ nghịch 3;4;5 tính giá trị từng phần?chia số 315 thành 3 phần tỉ lệ nghịch với 3:4:6. tính giá trị mỗi phần?4 cho tỉ lệ thức dfrac{a}{b}dfrac{c}{d} chứng minh rằnga)dfrac{a+b}{a-b}dfrac{c+d}{c-d}b)dfrac{5a+2c}{5a+2d}dfrac{a-4c}{b-4d}cdfrac{ab}{cd}dfrac{left(a+bright)^2}{left(...
Đọc tiếp
1 tìm các số hữu tỉ x,y thỏa mãn 3x=2y và x+y=-15
2 tìm các số hữu tỉ x,y biết rằng
a) x+y-z=20 và \(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{5}\)
b)\(\dfrac{x}{11}=\dfrac{y}{12};\dfrac{y}{3}=\dfrac{z}{7}\) và 2x-y+z=152
3) chia số 552 thành ba phần tỉ lệ nghịch 3;4;5 tính giá trị từng phần?
chia số 315 thành 3 phần tỉ lệ nghịch với 3:4:6. tính giá trị mỗi phần?
4 cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) chứng minh rằng
a)\(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
b)\(\dfrac{5a+2c}{5a+2d}=\dfrac{a-4c}{b-4d}\)
c\(\dfrac{ab}{cd}=\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}\)
Các bạn giúp mình với nhé mình dang cần gấp.mình xin cảm ơn
Bài 1:
Ta có: \(3x=2y\)
nên \(\dfrac{x}{2}=\dfrac{y}{3}\)
mà x+y=-15
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x+y}{2+3}=\dfrac{-15}{5}=-3\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=-3\\\dfrac{y}{3}=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=-9\end{matrix}\right.\)
Vậy: (x,y)=(-6;-9)
Đúng 1
Bình luận (0)
Bài 2:
a) Ta có: \(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{5}\)
mà x+y-z=20
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{x+y-z}{4+3-5}=\dfrac{20}{2}=10\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{4}=10\\\dfrac{y}{3}=10\\\dfrac{z}{5}=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=40\\y=30\\z=50\end{matrix}\right.\)
Vậy: (x,y,z)=(40;30;50)
Đúng 1
Bình luận (0)
Bài 2:
b) Ta có: \(\dfrac{y}{3}=\dfrac{z}{7}\)
nên \(\dfrac{y}{12}=\dfrac{z}{28}\)
mà \(\dfrac{x}{11}=\dfrac{y}{12}\)
nên \(\dfrac{x}{11}=\dfrac{y}{12}=\dfrac{z}{28}\)
hay \(\dfrac{2x}{22}=\dfrac{y}{12}=\dfrac{z}{28}\)
mà 2x-y+z=152
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{22}=\dfrac{y}{12}=\dfrac{z}{28}=\dfrac{2x-y+z}{22-12+28}=\dfrac{152}{38}=4\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{11}=4\\\dfrac{y}{12}=4\\\dfrac{z}{28}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=44\\y=48\\z=112\end{matrix}\right.\)
Vậy: (x,y,z)=(44;48;112)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tìm số hữu tỉ x biết:
a) |1-2x|>7
b) (x-2)(x+2)(4-x)(x-1)2 \(\le\)0
a) \(\left|1-2x\right|>7\)
<=> \(\orbr{\begin{cases}1-2x>7\\1-2x< -7\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< -3\\x>4\end{cases}}\)
b) Lập bảng:
Ta có: (x-2)(x+2)(4-x)(x-1)2 \(\le\)0
<=> \(\orbr{\begin{cases}-2\le x\le2\\x\ge4\end{cases}}\)
Tìm x, biết:
a) / x-2 / = 2x+1
b) / 2x-3 / + 2017 có giá trị nhỏ nhất
c) 199 - / x+3 / có gia strij lớn nhất
d) 37 - / 17.x+3/ không là số hữu tỉ âm, không là số hữu tỉ dương.
Tìm số hữu tỉ x , biết rằng :
( 2x - 1 )6 = ( 2x - 1 )8
( 2 - 3x )4 : (3x-2 )5
(2x-1)^6=(2x-1)^8'
=> (2x-1)=1 hoặc (2x-1)=0
(2x-1)=1 =>2x=2 =>x=1
(2x-1)=0 =>2x=1 =>x=0,5
Đúng 0
Bình luận (0)
\(\left(2x-1\right)^6=\left(2x-1\right)^8\)
\(\left(2x-1\right)^6-\left(2x-1\right)^8=0\)
\(\left(2x-1\right)^6-\left(2x-1\right)^6.\left(2x-1\right)^2=0\)
\(\left(2x-1\right)^6.\left[1-\left(2x-1\right)^2\right]=0\)
\(\left(2x-1\right)^6.\left[\left(1-2x+1\right)\left(1+2x-1\right)\right]=0\)
\(\left(2x-1\right)^6.\left[\left(2-2x\right).2x\right]=0\)
\(\left(2x-1\right)^6.\left[4x\left(1-x\right)\right]=0\)
\(\Rightarrow\orbr{\begin{cases}\left(2x-1\right)^6=0\\4x\left(1-x\right)=0\end{cases}}\Rightarrow\orbr{\begin{cases}2x-1=0\\4x=0hoac1-x=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=0hoacx=1\end{cases}}\)
vay \(x=\frac{1}{2}\)hoac \(\orbr{\begin{cases}x=0\\x=1\end{cases}}\)
\(\frac{\left(2-3x\right)^4}{\left(3x-2\right)^5}=\frac{-\left(3x-2\right)^4}{\left(3x-2\right)^5}=\frac{-1}{3x-2}\)
Đúng 0
Bình luận (0)
tìm hai số x và y biết x^2+y^2 ; x^2 - y^2 và x^2y^2 tỉ lệ nghịch với 1/25; 1/7; 1/576
Tìm x hữu tỉ biết: \(\frac{2x+\frac{2x^2}{x}}{3x}=\frac{3}{4}\)
Ta có: \(\frac{2x+\frac{2x^2}{x}}{3x}=\frac{3}{4}\)
\(\Rightarrow\frac{2x+2x}{3x}=\frac{3}{4}\)
\(\Leftrightarrow\frac{4x}{3x}=\frac{3}{4}\)
\(\Rightarrow x=\frac{16}{9}\)
Đúng 0
Bình luận (0)
theo mk thi x chỉ có thể bằng 0
giai ra ta dc \(\frac{4x}{3x}\)= \(\frac{3}{4}\)\(\Rightarrow\)16x=9x (vô li)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời