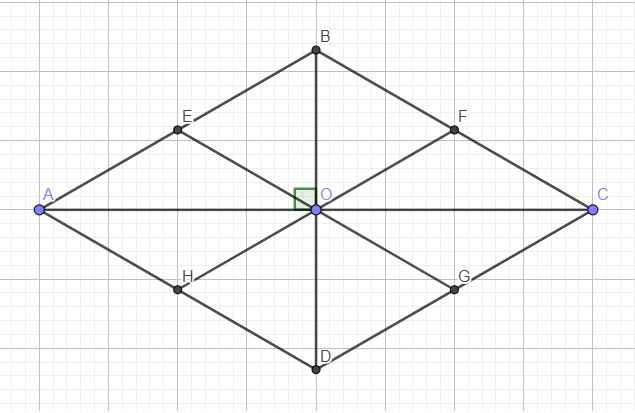
Cho hình thoi $ABCD$. Lấy $E, \, F$ trên $BC$ và $CD$ sao cho $BE=DF.$ Gọi $G, \, H$ lần lượt là giao điểm của $AE, \, AF$ với $BD.$ Chứng minh $AGCH$ là hình thoi.

Những câu hỏi liên quan
Bài 11: Cho hình thoi ABCD. Lấy E,F trên BC và CD sao cho BE=DF. Gọi G,H lần lượt là giao điểm của AE,AF với BD. Cm AGCH là hình thoi
ABCD là hình thoi
=>AC vuông góc BD tại trung điểm của mỗi đường và BD là phân giác của góc ABC
Xét ΔADF và ΔABE có
AD=AB
\(\widehat{ADF}=\widehat{ABE}\)
DF=BE
Do đó: ΔADF=ΔABE
=>AF=AE và \(\widehat{AFD}=\widehat{AEB}\)
Xét ΔHFD và ΔGEB có
\(\widehat{HFD}=\widehat{GEB};\widehat{FDH}=\widehat{EBG}\left(=\widehat{ABD}\right)\)
DF=BE
Do đó: ΔHFD=ΔGEB
=>HF=GE và DH=BG
AH+HF=AF
AG+GE=AE
mà HF=GE và AF=AE
nên AH=AG
Xét ΔCDH và ΔABG có
CD=AB
\(\widehat{CDH}=\widehat{ABG}\)
DH=BG
Do đó: ΔCDH=ΔABG
=>CH=AG
Xét ΔADH và ΔCBG có
AD=CB
\(\widehat{ADH}=\widehat{CBG}\)
DH=BG
Do đó: ΔADH=ΔCBG
=>AH=CG
Xét tứ giác AGCH có
AG=CH
AH=CG
Do đó: AGCH là hình bình hành
mà AC vuông góc GH
nên AGCH là hình thoi
Đúng 0
Bình luận (0)
Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE DF. Gọi G, H theo thứtựlà giao điểm của AE, AF với đường chéo BD. Chứng minh rằng tứgiác AGCH là hình thoi.*Gợi ý:+Gọi O là giao điểm của AC và BD+ Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD ta có:+Xét tam giác ABE và tam giác ADFAB .... ; 𝐵̂⋯; BE ...Suy ra: ∆ABE .... ( .........)Suy ra 𝐵𝐴𝐸̂⋯( 2 góc tương ứng)Mà AC là phân giác của góc 𝐵𝐴𝐷̂ 𝐸𝐴𝐶̂⋯(1)Do đó AO là phân giác của góc HAGXét ta...
Đọc tiếp
Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H theo thứtựlà giao điểm của AE, AF với đường chéo BD. Chứng minh rằng tứgiác AGCH là hình thoi.
*Gợi ý:
+Gọi O là giao điểm của AC và BD
+ Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD ta có:
+Xét tam giác ABE và tam giác ADFAB =.... ; 𝐵̂=⋯; BE =...
Suy ra: ∆ABE =.... ( .........)
Suy ra 𝐵𝐴𝐸̂=⋯( 2 góc tương ứng)
Mà AC là phân giác của góc 𝐵𝐴𝐷̂=> 𝐸𝐴𝐶̂=⋯(1)
Do đó AO là phân giác của góc HAG
Xét tam giác AGH có AO là đường phân giác, là đường cao
=> ∆AGH là tam giác cân tại A
=> HO =.... (2)
Vì ABCD là hình thoi nên AO =.... (3)
Từ(1), (2), (3) suy ra AGCH là hình thoi.
Cho hình thoi ABCD, lấy E trên BC, F trên CD, sao cho BE = BF. Gọi I,K theo thứ tự là giao điểm của AE;AF với đường chéo BD. Chứng minh rằng : AICK là hình thoi .
Cho hình bình hành ABCD. Trên cạnh AD, BC lần lượt lấy điểm H, G sao cho DH=BG a) Chứng minh: AGCH là hình bình hành. b) Gọi O là giao điểm của AC và BD. Chứng minh: G,O,H thẳng hàng c) Trên cạnh AB lấy điểm E, gọi F là giao điểm của EO với DC. Chứng minh:EGFH là hình bình hành
cho hình thoi ABCD có góc C=60°. gọi D là giao điểm AC và BD. Gọi E,F,G,H lần lượt là trung điểm AB,BC,CD,DA. Chứng minh rằng các điểm E,B,F,G,D,H cùng nằm trên một đường tròn
Do ABCD là hình thoi \(\Rightarrow\Delta BCD\) cân tại C
Mà \(C=60^0\Rightarrow\Delta BCD\) đều
Hoàn toàn tương tự, ta có tam giác ABD đều
\(\Rightarrow AB=BC=CD=DA=BD\) (1)
Gọi O là giao điểm 2 đường chéo \(\Rightarrow OA\perp OB\)
Trong tam giác vuông OAB, do E là trung điểm AB nên OE là trung tuyến ứng với cạnh huyền
\(\Rightarrow OE=\dfrac{1}{2}AB\) (2)
Mà O là trung điểm BD (tính chất hình thoi) \(\Rightarrow OB=\dfrac{1}{2}BD\) (3)
(1);(2);(3) \(\Rightarrow OE=OB\)
Hoàn toàn tương tự, ta có:
\(OE=OB=OF=OG=OD=OH\)
\(\Rightarrow\) Các điểm E, B, F, G, D, H cùng thuộc 1 đường tròn tâm O bán kính OB
Đúng 1
Bình luận (0)
1) cho hình thoi ABCD có góc C=60°. gọi D là giao điểm AC và BD. Gọi E,F,G,H lần lượt là trung điểm AB,BC,CD,DA. Chứng minh rằng các điểm E,B,F,G,D,H cùng nằm trên một đường tròn
Xét ΔABD có AB=AD và góc BAD=60 độ
nên ΔABD đều
Ta có: ΔDAB cân tại D
mà DE là đường trung tuyến
nên DE vuông góc với BE
=>E nằm trên đường tròn đường kính BD(1)
Ta có:ΔBAD cân tại B
ma BH là đường trung tuyến
nên BH vuông góc với HD
=>H nằm trên đường tròn đường kính BD(2)
Xét ΔCBD có CB=CD và góc BCD=60 độ
nên ΔCBD đều
Ta có: ΔBDC cân tại D
mà DF là đường trung tuyến
nen DF vuông góc với BF
=>F nằm trên đường tròn đường kính BD(3)
Ta có: ΔBDC cân tại B
mà BG là đường trung tuyến
nên BG vuông góc với GD
=>G nằm trên đường tròn đường kính BD(4)
Từ (1), (2), (3) và (4) suy ra E,B,F,G,D,H cùng nằm trên 1 đường tròn
Đúng 0
Bình luận (0)
Cho hình thang ABCD có CD=3AB .Trên CD lấy E,F sao cho CE=EF =FD. Chứng minh
a, ABFD là hình bình hành
b, AF//BE
c,AE=BC
d, Gọi M,N,P lần lượt là trung điểm của AF và BD ,AE và PF, AC và BE .Chứng minh M,N,P thẳng hàng
a) Ta có: DF=FE=CE(gt)
mà DF+FE+CE=DC
nên \(DF=FE=CE=\dfrac{DC}{3}\)
Xét tứ giác ABFD có
AB//FD(gt)
AB=FD
Do đó: ABFD là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Xét tứ giác ABEF có
AB//EF(gt)
AB=EF(cmt)
Do đó: ABEF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Suy ra: AF=BE(Hai cạnh đối)
Đúng 1
Bình luận (0)
c) Xét tứ giác ABCE có
AB//CE
AB=CE
Do đó: ABCE là hình bình hành
Suy ra: AE=BC
Đúng 0
Bình luận (0)
cho hình bình hành ABCD .Trên đường thẳng AC lấy 2 điểm E,F sao cho AE=AF=FC. Gọi O là giao điểm của AC và BD
cm DF cắt BC tại I , BEDC là hình bình hành . Chứng minh DF= 2FM
Cho hình thoi ABCD, lấy E trên BC, F trên CD, sao cho BE = BF. Gọi I,K theo thứ tự là giao điểm của AE;AF với đường chéo BD. Chứng minh rằng : AICK là hình thoi .