Hãy ước lượng sai số tuyệt đối \({\Delta _{{S_1}}}\) ở Ví dụ 1.

Những câu hỏi liên quan
Ở Babylon, một tấm đất sét có niên đại khoảng 1900 – 1600 trước Công nguyên đã ghi lại một phát biểu hình học, trong đó ám chỉ ước lượng số \(\pi \) bằng \(\frac{{25}}{8} = 3,1250.\) Hãy ước lượng sai số tuyệt đối và sai số tương đối của giá trị gần đúng này, biết \(3,141 < \pi < 3,142.\)
Ta có: \(3,141 < \pi < 3,142 \Rightarrow 3,141 - 3,125 < \pi - 3,125 < 3,142 - 3,125\)
Hay \(0,016 < \pi - 3,125 < 0,017 \Rightarrow 0,016 < \left| {\pi - 3,125} \right| < 0,017\)
Sai số tuyệt đối của số gần đúng 3,125: \(0,016 < {\Delta _{3,125}} < 0,017\)
Sai số tương đối \({\delta _{3,125}} = \frac{{{\Delta _{3.125}}}}{{\left| {3,125} \right|}} < \frac{{0,017}}{{3,125}} = 0,0544\% \)
Đúng 0
Bình luận (0)
CHo : π=3,141592654
a) Quy tròn hàng phần chục,ước lượng sai sô tuyệt đối
b) Quy tròn hàng phần trăm,ước lượng sai số tuyệt đối
c) Quy tròn hàng phần nghìn và ước lượng sai số tuyệt đối
Bảng 3.4 thể hiện kết quả đo khối lượng của một túi trái cây bằng cân đồng hồ. Em hãy xác định sai số tuyệt đối ứng với từng lần đo, sai số tương đối của phép đo. Biết sai số dụng cụ là 0,1 kg.Sai số tuyệt đối của phép đo: Delta m overline {Delta m} + Delta {m_{dc}} ?Sai số tương đối của phép đo: delta m frac{{Delta m}}{{overline m }}.100% ?Kết quả phép đo: m overline m pm Delta m ?
Đọc tiếp
Bảng 3.4 thể hiện kết quả đo khối lượng của một túi trái cây bằng cân đồng hồ. Em hãy xác định sai số tuyệt đối ứng với từng lần đo, sai số tương đối của phép đo. Biết sai số dụng cụ là 0,1 kg.
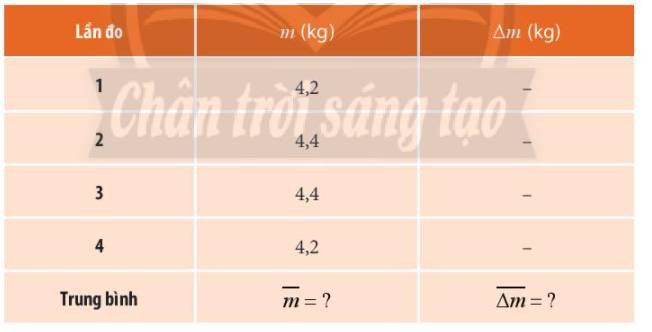
Sai số tuyệt đối của phép đo: \(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = ?\)
Sai số tương đối của phép đo: \(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = ?\)
Kết quả phép đo: \(m = \overline m \pm \Delta m = ?\)
Giá trị trung bình khối lượng của túi trái cây là:
\(\overline m = \frac{{{m_1} + {m_2} + {m_3} + {m_4}}}{4} = \frac{{4,2 + 4,4 + 4,4 + 4,2}}{4} = 4,3(kg)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {m_1} = \left| {\overline m - {m_1}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\\\Delta {m_2} = \left| {\overline m - {m_2}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_3} = \left| {\overline m - {m_3}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_4} = \left| {\overline m - {m_4}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta m} = \frac{{\Delta {m_1} + \Delta {m_2} + \Delta {m_3} + \Delta {m_4}}}{4} = \frac{{0,1 + 0,1 + 0,1 + 0,1}}{4} = 0,1(kg)\)
Sai số tuyệt đối của phép đo là:
\(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = 0,1 + 0,1 = 0,2(kg)\)
Sai số tương đối của phép đo là:
\(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = \frac{{0,2}}{{4,2}}.100\% = 4,65\% \)
Kết quả phép đo:
\(m = \overline m \pm \Delta m = 4,3 \pm 0,2(kg)\)
Đúng 0
Bình luận (0)
Cho b = 3,14 và c = 3,1416 là những giá trị gần đúng của π. Hãy ước lượng sai số tuyệt đối của b và c.
π = 3,14159265358…
+ Viết b = 3,14 :
Sai số tuyệt đối : |b – π| < |3,14 – 3,14159265358| < 0,0016
Vậy sai số tuyệt đối của b không quá 0,0016.
+ Viết c = 3,1416 :
Sai số tuyệt đối : |c – π| < |3,1416 – 3,14159265358| = 0,00001.
Vậy sai số tuyệt đối của c không vượt quá 0,00001.
Đúng 0
Bình luận (0)
Thế nào là địa chỉ tương đối, địa chỉ tuyệt đối, địa chỉ hỗn hợp? Hãy cho ví dụ.
- Địa chỉ tương đối là dạng địa chỉ có thể thay đổi cả tên hàng và tên cột khi sao chép công thức sang nơi khác
- Địa chỉ tuyệt đối: dạng địa chỉ có cả tên hàng và tên cột không bị thay đổi khi sao chép công thức sang nơi khác
- Địa chỉ hỗn hợp: dạng địa chỉ có tên hàng và tên cột thay đổi khi sao chép công thức sang nơi khác.
Đúng 1
Bình luận (0)
Thế nào là địa chỉ tương đối, địa chỉ tuyệt đối, địa chỉ hỗn hợp? Hãy cho ví dụ.
Địa chỉ tương đối: Địa chỉ tương đối chỉ định tới một ô hoặc vùng dữ liệu dựa trên vị trí tương đối của nó so với ô hiện tại. Khi bạn sao chép công thức hoặc kéo công thức xuống các ô khác, địa chỉ tương đối sẽ được cập nhật tự động để tham chiếu đến các ô mới mà công thức đang được sao chép.
Ví dụ: Nếu bạn có công thức "=A1+B1" trong ô C1 và sao chép nó xuống ô C2, công thức sao chép sẽ tự động thay đổi thành "=A2+B2" để tham chiếu đến ô và vùng dữ liệu mới.
Địa chỉ tuyệt đối: Địa chỉ tuyệt đối chỉ định tới một ô hoặc vùng dữ liệu cố định mà không bị thay đổi khi công thức được sao chép hoặc kéo.
Ví dụ: Nếu bạn có công thức "=A$1+B$1" trong ô C1 và sao chép nó xuống ô C2, công thức sao chép sẽ giữ nguyên địa chỉ tuyệt đối và không thay đổi thành "=A$1+B$2".
Địa chỉ hỗn hợp: Địa chỉ hỗn hợp sử dụng một sự kết hợp giữa địa chỉ tương đối và địa chỉ tuyệt đối. Với địa chỉ hỗn hợp, một phần của địa chỉ được cố định và phần còn lại được cập nhật khi công thức được sao chép hoặc kéo.
Ví dụ: Nếu bạn có công thức "=A$1+B2" trong ô C1 và sao chép nó xuống ô C2, phần địa chỉ tương đối (B2) sẽ được cập nhật thành B3, trong khi phần địa chỉ tuyệt đối (A$1) sẽ giữ nguyên không thay đổi.
Đúng 1
Bình luận (0)
Gõ dấu đô la trên hoc24 sẽ bị lỗi sang định dạng LaTex, nên mình gửi lại dạng ảnh nhé!

Đúng 1
Bình luận (0)
Đánh giá sai số tương đối của khối lượng bao gạo được đóng gói theo hai dây chuyền A, B ở Ví dụ 2 và HĐ4. Dựa trên tiêu chí này, dây chuyền nào tốt hơn?
Xét dây chuyền A: ta có d=0,2; a=5.
\({\delta _5} \le \frac{{0,2}}{{\left| 5 \right|}} = 0,04 = 4\% \)
Xét dây chuyền B: ta có d=0,5; a=20
\({\delta _5} \le \frac{{0,5}}{{\left| {20} \right|}} = 0,025 = 2,5\% \)
Ta thấy \(2,5\% < 4\% \) nên dây chuyền B tốt hơn.
Chú ý
Có thể không cần đổi sang đơn vị phần trăm (%) để so sánh.
Đúng 0
Bình luận (0)
Biết ∛5 = 1,709975947.....
Viết gần đúng ∛5 theo nguyên tắc làm tròn với hai, ba, bốn chữ số thập phân và ước lượng sai số tuyệt đối.
– Làm tròn với hai chữ số thập phân: ∛5 = 1,71.
Sai số tuyệt đối: |1,71 – ∛5| < |1,71 – 1,7099| = 0,0001.
Vậy sai số tuyệt đối không vượt quá 0,0001.
– Làm tròn với ba chữ số thập phân: ∛5 = 1,710
Sai số tuyệt đối: |1,71 – ∛5| < |1,71 – 1,7099| = 0,0001.
Vậy sai số tuyệt đối không vượt quá 0,0001.
– Làm tròn với bốn chữ số thập phân: ∛5 = 1,7100
|1,71 – ∛5| < |1,71 – 1,7099| = 0,0001.
Vậy sai số tuyệt đối không vượt quá 0,0001.
Đúng 0
Bình luận (0)
Cho biết 2 = 1,4142135... . Viết gần đúng số 2 theo quy tắc làm tròn đến hàng phần nghìn, sai số tuyệt đối mắc phải ước lượng được là:
A. 0,01
B. 0,002
C. 0,004
D. 0,001













