Thiết kế một chóa đèn có mặt cắt hình parabol với kích thước được cho trong hình sau:

Áp dụng tính chất quang học của parabol để giải quyết vẫn đề sau đây:
Một đèn pin có chóa đèn có mặt cắt hình parabol với kích thước như trong hình 21.
a) Chọn hệ trục tọa độ Oxy sao cho gốc O là đỉnh của parabol và trục Ox đi qua tiêu điểm. Viết phương trình của parabol trong hệ tọa độ vừa chọn.
b) Để đèn chiếu được xa phải đặt bóng đèn cách đỉnh của chóa đèn bao nhiêu xentimét.

a) Vẽ lại hình vẽ như dưới đây

Ta có \(AB = 18,x = 3 \Rightarrow A(3;9)\)
Gọi phương trình parabol tổng quát \({y^2} = 2px\)
Thay tọa độ điểm A vào phương trình ta có: \({9^2} = 2p.3 \Rightarrow p = \frac{{27}}{2}\)
Vậy phương trình parabol trên hệ trục tọa độ vừa chọn là \({y^2} = 27x\)
b) Từ câu a) ta có: \(p = \frac{{27}}{2}\)
Suy ra tiêu điểm của parabol là \(F\left( {\frac{{27}}{4};0} \right)\)
Vậy để đèn chiếu được xa phải đặt bóng đèn cách đỉnh của chóa đèn \(\frac{{27}}{4}\) xentimét
Từ một nguyên vật liệu cho trước, một công ty muốn thiết kế bao bì để đựng sữa với thể tích 1dm3. Bao bì được thiết kế bởi một trong hai mô hình sau: hình hộp chữ nhật có đáy là hình vuông; hoặc hình trụ. Hỏi thiết kế theo mô hình nào sẽ tiết kiệm được nguyên vật liệu nhất? Và thiết kế mô hình đó theo kích thước như thế nào?


Để kỷ niệm ngày 26-3. Chi đoàn 12A dư định dưng một lều trại có dạng parabol (nhìn từ mặt trước, lều trại được căng thẳng từ trước ra sau, mặt sau trại cũng là parabol có kích thước giống như mặt trước) với kích thước. nền trại là một hình chữ nhật có chiều rộng là 3 mét, chiều sâu là 6 mét, đỉnh của parabol cách mặt đất là 3 mét. Hãy tính thể tích phần không gian phía trong trại để lớp 12A cử số lượng người tham dư trại cho phù hợp.
A. 30 m3
B. 36 m3
C. 40 m3
D. 41 m3
Chọn B.
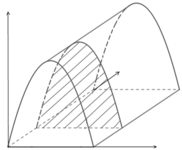
Phương pháp: Sử dụng tích phân.
Cách giải: Chọn hệ trục tọa độ như hình sao cho mặt trước của lều là mặt (Oxy), mặt đáy lều là mặt (Oyz).

Để kỷ niệm ngày 26-3. Chi đoàn 12A dư định dựng một lều trại có dạng parabol (nhìn từ mặt trước, lều trại được căng thẳng từ trước ra sau, mặt sau trại cũng là parabol có kích thước giống như mặt trước) với kích thước. nền trại là một hình chữ nhật có chiều rộng là 3 mét, chiều sâu là 6 mét, đỉnh của parabol cách mặt đất là 3 mét. Hãy tính thể tích phần không gian phía trong trại để lớp 12A cử số lượng người tham dư trại cho phù hợp
![]()
![]()
![]()
![]()
Một bồn nước được thiết kế với chiều cao 8dm, ngang 8dm và dài 2m. Bề mặt cong đều nhau và mặt cắt ngang là một hình parabol như hình vẽ dưới
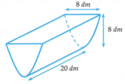
Hỏi bồn chứa được tối đa bao nhiêu lít nước?
A. 1280 3 l í t
B. 1280 π lít
C. 2560 3 l í t
D. 1280 (lít)
Chọn đáp án C
Xét mặt cắt là một hình parabol, chọn hệ trục tọa độ như hình vẽ bên.
Phương trình parabol (P) có dạng y = a x 2 với a > 0 .
Ta thấy (P) đi qua các điểm (-4; 8) và (4; 8) nên a = 1 2 .
Suy ra phương trình parabol (P) là y = 1 2 x 2
Diện tích mặt cắt parabol của bồn nước cùng chính là diện tích của hình phẳng được giới hạn bởi các đường y = 1 2 x 2 và y = 8.
Diện tích đó là:
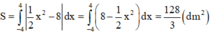
Do đó thể tích của bồn nước là: V = 2560 3 d m 3
Một vật có kích thước và hình dáng như hình vẽ dưới đây. Đáy là hình tròn giới hạn bởi đường tròn x 2 + y 2 = 16 (nằm trong mặt phẳng Oxy), cắt vật bởi các mặt phẳng vuông góc với trục Ox ta được thiết diện là hình vuông. Thể tích của vật thể là
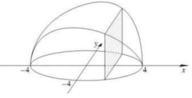
A. ∫ − 1 4 4 16 − x 2 d x
B. ∫ − 4 4 4 π x 2 d x
C. ∫ − 4 4 4 x 2 d x
D. ∫ − 4 4 4 π 16 − x 2 d x
Một kĩ sư được một công ty xăng dầu thuê thiết kế một mẫu bồn cầu chứa xăng với thể tích V cho trước, hình dạng như hình bên, các kích thước r, h thay đổi sao cho nguyên vật liệu làm bồn xăng là ít nhất.
Người kĩ sư này phải thiết kế kích thước h như thế nào để đảm bảo được đúng yêu cầu mà công ty xăng dầu đã đưa ra
![]()
![]()
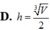
Người thợ làm một cái bể cá hai ngăn không nắp với thể tích 1,296 m3. Người thợ này cắt các tấm kính ghép lại một bể cá dạng hình hộp chữ nhật với ba kích thước a,b,c như hình vẽ. Hỏi người thợ phải thiết kế các kích thước a, b, c bằng bao nhiêu mét để đỡ tốn kính nhất. Giả thiết rằng độ dày của của kính không đáng kể.
Một khuôn viên dạng nửa hình tròn có đường kính bằng 4 5 (m). Trên đó người thiết kế hai phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa hình tròn và hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu), cách nhau một khoảng bằng 4 (m), phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là 100.000 đồng/ m 2 . Hỏi cần bao nhiêu tiền để trồng cỏ Nhật Bản trên phần đất đó? (Số tiền được làm tròn đến hàng nghìn)

A. 3.895.000 đồng.
B. 1.948.000 đồng.
C. 2.388.000 đồng.
D. 1.194.000 đồng.
Đáp án B.
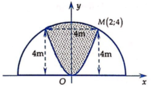 Đặt hệ trục tọa độ như hình vẽ. Khi đó phương trình nửa đường tròn là
y
=
R
2
-
x
2
=
2
5
2
-
x
2
=
20
-
x
2
.
Đặt hệ trục tọa độ như hình vẽ. Khi đó phương trình nửa đường tròn là
y
=
R
2
-
x
2
=
2
5
2
-
x
2
=
20
-
x
2
.
Phương trình parabol (P) có đỉnh là gốc O sẽ có dạng y = a x 2 . Mặt khác (P) qua điểm M(2;4) do đó 4 = a . - 2 2 ⇔ a = 1 .
Phần diện tích của hình phẳng giới hạn bởi (P) và nửa đường tròn (phần tô màu) là S 1 = ∫ - 2 2 20 - x 2 - x 2 d x ≈ 11 , 94 ( m 2 ) .
Phần diện tích trồng cỏ là: S t r o n g c o = 1 2 S h i n h t r o n - S 1 ≈ 19 , 47592654 m 2 .
Vậy số tiền cần có là S t r o n g c o × 100000 ≈ 1948000 (đồng).