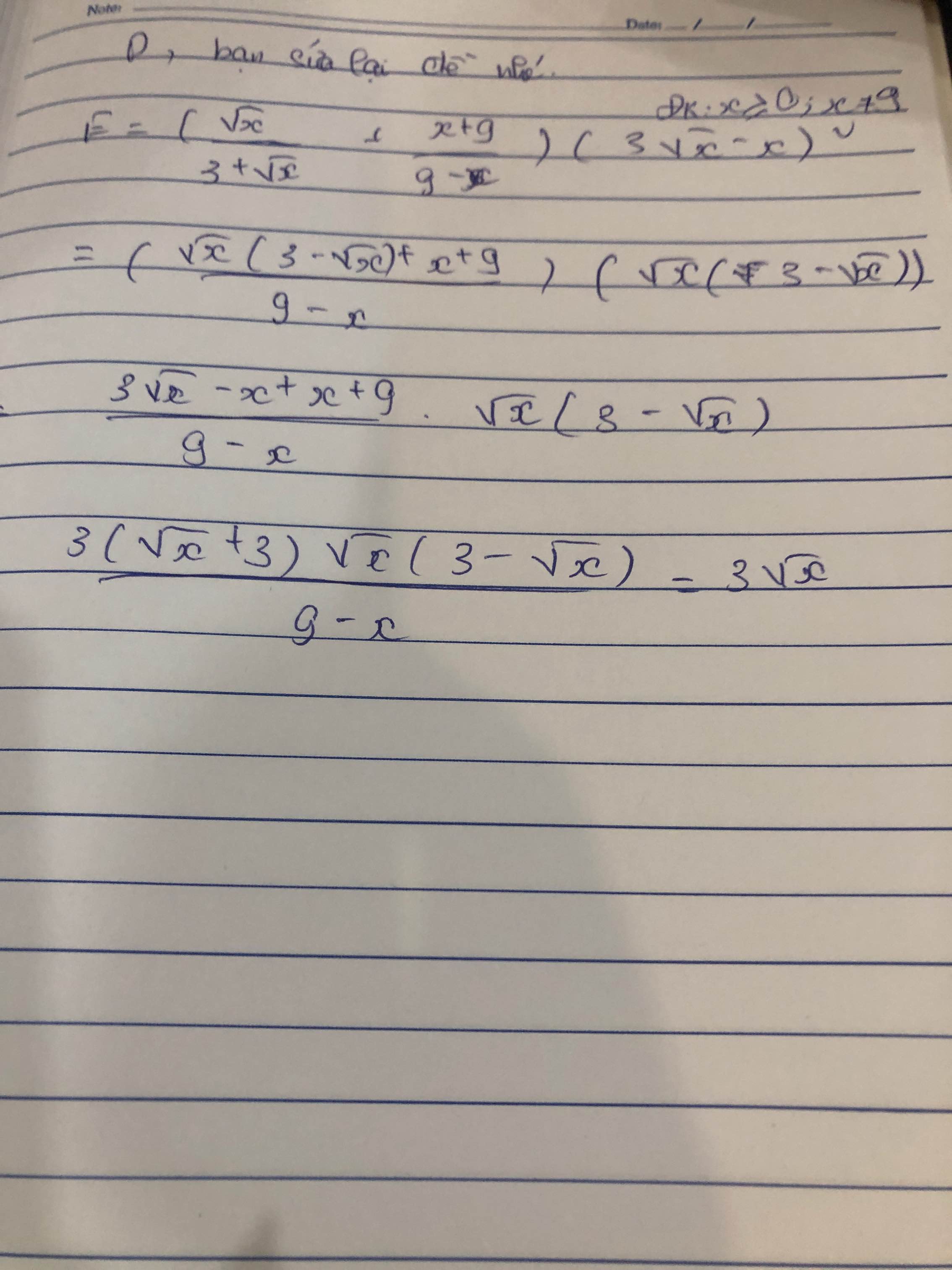\(\hept{\begin{cases}\left(x+\frac{2019}{2020}\right)^{100}\ge0\\\left(y-\frac{9}{11}\right)^{200}\ge0\end{cases}}\Rightarrow\hept{\begin{cases}x+\frac{2019}{2020}=0\\y-\frac{9}{11}\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{-2019}{2020}\\y=\frac{9}{11}\end{cases}}\)

Ta có : \(\left[x+\frac{2019}{2020}\right]^{100}\ge0\forall x\)

\(\left[y-\frac{9}{11}\right]^{200}\ge0\forall y\)

\(\Leftrightarrow\left[x+\frac{2019}{2020}\right]^{100}+\left[y-\frac{9}{11}\right]^{200}\ge0\forall x,y\)

Dấu " = " xảy ra khi : \(\hept{\begin{cases}x+\frac{2019}{2020}=0\\y-\frac{9}{11}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-\frac{2019}{2020}\\y=\frac{9}{11}\end{cases}}\)

Ta có: \(P\left(x\right)=x^5+ax^4+bx^3+cx^2+dx+e\)

Suy ra \(P\left(1\right)=1^5+a\cdot1^4+b\cdot1^3+c\cdot1^2+d\cdot1+e=1\)

\(\Rightarrow a+b+c+d+e=0\)

\(P\left(2\right)=2^5+a\cdot2^4+b\cdot2^3+c\cdot2^2+d\cdot2+e=4\)

\(\Rightarrow16a+8b+4c+2d+e+28=0\)

\(P\left(3\right)=3^5+a\cdot3^4+b\cdot3^3+c\cdot3^2+d\cdot3+e=9\)

\(\Rightarrow81a+27b+9c+3d+e+234=0\)

\(P\left(4\right)=4^5+a\cdot4^4+b\cdot4^3+c\cdot4^2+d\cdot4+e=16\)

\(\Rightarrow256a+64b+16c+4d+e+1008=0\)

\(P\left(5\right)=5^5+a\cdot5^4+b\cdot5^3+c\cdot5^2+d\cdot5+e=25\)

\(\Rightarrow625a+125b+25c+5d+e+999=0\)

Thay lẫn lộn vào nhau đi nhé

Cho phép lm tiếp....

\(\Rightarrow\left\{{}\begin{matrix}15a+7b+3c+d=-28\\80a+26b+8c+2d=-234\\255a+63b+15c+3d=-1008\\624a+124b+24c+4d=-3100\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}50a-12b+2c=-178\\210a+42b+6c=-924\\564a+96b+12c=-2988\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a=-15\\b=85\\c=-224\end{matrix}\right.\)

Thay bào pt \(15a+7b+3c+d=-28\) ta có: \(-225+595-672+d=-28\Rightarrow d=274\)

Thay vào pt \(a+b+c+d+e=0\) ta có:

\(-15+85-224+274+e=0\Rightarrow e=-120\)

Thay a,b,c,d,e vào r` tính là ra!

p/s: cho a,b,c bấm casio nhé!

Cách khác:

Tìm đa thức phụ: giả sử có đa thức:

\(\:ax^2+bx+c\)

Ta có: \(\left\{{}\begin{matrix}P\left(1\right)=a\cdot1^2+b\cdot1+c=1\\P\left(2\right)=a\cdot2^2+b\cdot2+c=4\\P\left(3\right)=a\cdot3^2+b\cdot3+c=9\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b+c=1\\4a+2b+c=4\\9a+3b+c=9\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a=1\\b=0\\c=0\end{matrix}\right.\)

\(\Rightarrow\:ax^2+bx+c=1\cdot x^2+0\cdot x+0=x^2\)

\(\Rightarrow P\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-4\right)\left(x-5\right)+x^2\)

Tới đây thay từng x vào r` tính....

Sửa lại đề là tìm Max nhé m.n

Ta có:

\(\frac{ab+bc+ca+6\left(a+b+c\right)+27}{\left(a+3\right)\left(b+3\right)\left(c+3\right)}=\frac{3}{5}\)

\(\Leftrightarrow\frac{\left(b+3\right)\left(c+3\right)+\left(c+3\right)\left(a+3\right)+\left(a+3\right)\left(b+3\right)}{\left(a+3\right)\left(b+3\right)\left(c+3\right)}=\frac{3}{5}\)

\(\Leftrightarrow\frac{5}{a+3}+\frac{5}{b+3}+\frac{5}{c+3}=3\Leftrightarrow\frac{a-2}{a+3}+\frac{b-2}{b+3}+\frac{c-2}{c+3}=0\)

Xét biểu thức:

\(\frac{a^2-4}{a^2-9}=\frac{\left(a-2\right)\left(a+2\right)}{\left(a-3\right)\left(a+3\right)}=\frac{a-2}{a+3}.\frac{a+2}{a-3}\)

tưởng tự:

\(\frac{b^2-4}{b^2-9}=\frac{b-2}{b+3}.\frac{b+2}{b-3},\frac{c^2-4}{c^2-9}=\frac{c-2}{c+3}.\frac{c+2}{c-3}\)

\(\Rightarrow\frac{a^2-4}{a^2-9}+\frac{b^2-4}{b^2-9}+\frac{c^2-4}{c^2-9}=\frac{a-2}{a+3}.\frac{a+2}{a-3}+\frac{b-2}{b+3}.\frac{b+2}{b-3}+\frac{c-2}{c+3}.\frac{c+2}{c-3}\)

Do vai trò của a và b và c như nhau nên ta giả sử

\(a\ge b\ge c\)

Khi đó ta có:

\(\frac{a-2}{a+3}\ge\frac{b-2}{b+3}\ge\frac{c-2}{c+3},\frac{a+2}{a-3}\le\frac{b+2}{b-3}\le\frac{c+2}{c-3}\)

Áp dụng bất đẳng thức chebyshev cho 2 bộ ngược chiều trên ta có
\(\frac{a-2}{a+3}.\frac{a+3}{a-2}+\frac{b-2}{b+3}.\frac{b+2}{b-3}+\frac{c-2}{c+3}.\frac{c+2}{c-3}\le\left(\frac{a-2}{a+3}+\frac{b-2}{b+3}+\frac{c-2}{c+3}\right).\left(\frac{a+2}{a-3}+\frac{b+2}{b-3}+\frac{c+2}{c-3}\right)\)

Mà \(\frac{a-2}{a+3}+\frac{b-2}{b+3}+\frac{c-2}{c+3}=0\)

\(\Rightarrow\frac{a^2-4}{a^2-9}+\frac{b^2-4}{b^2-9}+\frac{c^2-4}{c^2-9}\le0\)

\(\Rightarrow\frac{5}{a^2-9}+\frac{5}{b^2-9}+\frac{5}{c^2-9}\le-3\Rightarrow\frac{1}{a^2-9}+\frac{1}{b^2-9}+\frac{1}{c^2-9}\le\frac{-3}{5}\)

Dấu bằng xảy ra khi a=b=c=2

Tìm max nha mấy god, e bị nhầm sory

 e sửa lại hahaha, bất đẳng thức chebyshev áp dụng v là ko đúng, phải lớn hơn hoặc bằng ạ, e cứ bị nhầm dấu, lần đầu đã ok r sau lại còn sửa hjhj

Gọi M(x,y) 

Trong (E) có : \(c=\sqrt{a^2-b^2}=\sqrt{5}\)

Từ đó ta có : \(F_1\left(\sqrt{5};0\right);F_2\left(-\sqrt{5};0\right)\); \(F_1F_2=2\sqrt{5}\) 

=> \(\overrightarrow{F_1M}\left(x-\sqrt{5};y\right)\Rightarrow F_1M^2=\left(x-\sqrt{5}\right)^2+y^2\)

tương tự \(F_2M^2=\left(x+\sqrt{5}\right)^2+y^2\)

Do \(\widehat{F_1MF_2}=90^{\text{o}}\) nên tam giác F₁MF₂ vuông tại M

=> F₁M² + F₂M² = F₁F₂²

<=>  \(\left(x-\sqrt{5}\right)^2+y^2+\left(x+\sqrt{5}\right)^2+y^2=20\)

\(\Leftrightarrow x^2+y^2=5\)

Lại có \(M\in\left(E\right)\Rightarrow\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)

từ đó ta có hệ \(\left\{{}\begin{matrix}x^2+y^2=5\\\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2=\dfrac{9}{5}\\y^2=\dfrac{16}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\pm\dfrac{3\sqrt{5}}{5}\\y=\pm\dfrac{4\sqrt{5}}{5}\end{matrix}\right.\)

Vậy có 4 điểm hấp dẫn yêu cầu bài toán:

Phương trình của elip (E) là \frac{x^{2}}{9} + \frac{y^{2}}{4} = 1. Từ đây, ta có:

• a^{2} = 9 ⇒ a = 3

• b^{2} = 4 ⇒ b = 2

• c^{2} = a^{2}-b^{2} = 9-4 = 5 ⇒ c = \sqrt{5}

Vậy, hai tiêu điểm của elip là F_{1}(-\sqrt{5},0) và F_{2}(\sqrt{5},0).

Gọi M(x,y) là điểm thuộc elip (E). Vì M thuộc (E) nên tọa độ của M thỏa mãn phương trình elip:

\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1

Vì ∠F_{1}MF_{2} = 90^{\circ }, tam giác F_{1}MF_{2} vuông tại M. Do đó, theo định lý Pythagoras, ta có:

F_{1}M^{2} + F_{2}M^{2} = F_{1}F^{2}_{2}

Ta có:

• F_{1}M^{2} = (x + \sqrt{5})^{2} + y^{2} = x^{2} + 2\sqrt{5}x + 5 + y^{2}

• F_{2}M^{2} = (x-\sqrt{5})^{2} + y^{2} = x^{2}-2\sqrt{5}x + 5 + y^{2}

• F_{1}F^{2}_{2} = (2\sqrt{5})^{2} = 20

Thay vào phương trình Pythagoras:

(x^{2} + 2\sqrt{5}x + 5 + y^{2}) + (x^{2}-2\sqrt{5}x + 5 + y^{2}) = 20

2x^{2} + 2y^{2} + 10 = 20

2x^{2} + 2y^{2} = 10

x^{2} + y^{2} = 5

Ta có hệ phương trình:

\left\{ \, \begin{cases}\textstyle \frac{x^{2}}{9}+\frac{y^{2}}{4}=1\\ \textstyle x^{2}+y^{2}=5\end{cases}\right.

Từ phương trình thứ hai, ta có y^{2} = 5-x^{2}. Thay vào phương trình thứ nhất:

\frac{x^{2}}{9} + \frac{5-x^{2}}{4} = 1

4x^{2} + 9(5-x^{2}) = 36

4x^{2} + 45-9x^{2} = 36

-5x^{2} = -9

x^{2} = \frac{9}{5}

x = ± \frac{3}{\sqrt{5}} = ± \frac{3\sqrt{5}}{5}

Với x^{2} = \frac{9}{5}, ta có y^{2} = 5-\frac{9}{5} = \frac{25-9}{5} = \frac{16}{5}

y = ± \frac{4}{\sqrt{5}} = ± \frac{4\sqrt{5}}{5}

Vậy, có bốn điểm M thỏa mãn điều kiện đề bài:

M_{1}\left( \frac{3\sqrt{5}}{5},\frac{4\sqrt{5}}{5}\right) ,M_{2}\left( \frac{3\sqrt{5}}{5},-\frac{4\sqrt{5}}{5}\right) ,M_{3}\left( -\frac{3\sqrt{5}}{5},\frac{4\sqrt{5}}{5}\right) ,M_{4}\left( -\frac{3\sqrt{5}}{5},-\frac{4\sqrt{5}}{5}\right)

d: \(=\dfrac{-7}{9}\left(\dfrac{3}{11}+\dfrac{8}{11}\right)+1+\dfrac{7}{9}=1\)

e: \(=\dfrac{1}{5}\left(\dfrac{10}{19}+\dfrac{9}{19}\right)-\dfrac{2}{35}=\dfrac{1}{5}-\dfrac{2}{35}=\dfrac{5}{35}=\dfrac{1}{7}\)

f: \(=\left(-25\cdot4\right)\cdot\left(-8\cdot125\right)\cdot\left(-17\right)=-1700000\)

Tim Max nha

bóp phít