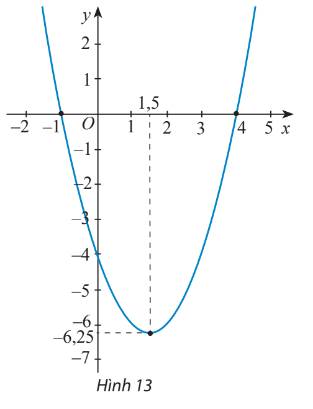
Tìm công thức của hàm số bậc hai có đồ thị như Hình 13.
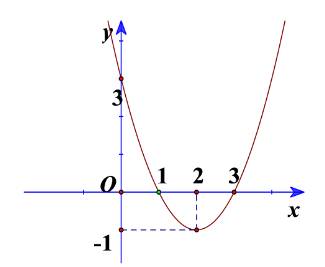
Một hàm số bậc hai có đồ thị như hình vẽ bên. Công thức biểu diễn hàm số đó là:

A. y = - x 2 + 2 x
B. y = - x 2 + 2 x + 1
C. y = x 2 - 2 x
D. y = x 2 - 2 x + 1
Gọi phương trình của đồ thị hàm số là y = a x 2 + b x + c .
Dựa vào hình vẽ, ta thấy đồ thị hàm số đi qua các điểm O(0; 0); (1; -1) và(2; 0).
Thay tọa độ các điểm này vào phương trình hàm số ta được hệ phương trình:
0 = a .0 2 + b .0 + c − 1 = a .1 2 + b .1 + c 0 = a .2 2 + b .2 + c ⇔ c = 0 a + b + c = − 1 4 a + 2 b + c = 0 ⇔ a = 1 b = − 2 c = 0
Phương trình đồ thị hàm số là y = x 2 – 2 x
Đáp án C
Cho đồ thị hàm số bậc hai ở Hình 15.
a) Xác định trục đối xứng, tọa độ đỉnh của đồ thị hàm số.
b) Xác định khoảng đồng biến, khoảng nghịch biến của hàm số.
c) Tìm công thức xác định hàm số.
a) Trục đối xứng là đường thẳng \(x = 2\)
Đỉnh là \(I\left( {2; - 1} \right)\)
b) Từ đồ thị ta thấy trên khoảng \(\left( { - \infty ;2} \right)\) thì hàm số đi xuống nên hàm số nghịch biến trên \(\left( { - \infty ;2} \right)\).
Trên khoảng \(\left( {2; + \infty } \right)\) thì hàm số đi xuống nên đồng biến trên \(\left( {2; + \infty } \right)\).
c) ) Gọi hàm số là \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Đồ thị hàm số có đỉnh là \(I\left( {2; - 1} \right)\) nên ta có:
\(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\a{.2^2} + b.2 + c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2b + c = - 1\end{array} \right.\)
Ta lại có điểm \(\left( {1;0} \right)\) thuộc đồ thị nên ta có: \(a + b + c = 0\)
Vậy ta có hệ sau:
\(\left\{ \begin{array}{l}b = - 4a\\4a + 2b + c = - 1\\a + b + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2.\left( { - 4a} \right) + c = - 1\\a + \left( { - 4a} \right) + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\c - 4a = - 1\\c - 3a = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\a = 1\\c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4\\a = 1\\c = 3\end{array} \right.\)
Vậy parabol là \(y = {x^2} - 4x + 3\)
Cho hàm số y = f(x) và hàm số bậc ba y = g(x) có đồ thị như hình vẽ bên. Diện tích phần gạch chéo được tính bởi công thức nào sau đây?
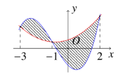
A . S = ∫ - 3 - 1 [ f ( x ) - g ( x ) ] dx + ∫ - 1 2 [ g ( x ) - f ( x ) ] dx
B . S = | ∫ - 3 2 [ f ( x ) - g ( x ) ] dx |
C. S = ∫ - 3 - 1 [ g ( x ) - f ( x ) ] dx + ∫ - 1 2 [ f ( x ) - g ( x ) ] dx
D. S = ∫ - 3 - 1 [ g ( x ) - f ( x ) ] dx + ∫ - 1 2 [ g ( x ) - f ( x ) ] dx
Cho hàm số đa thức bậc ba y=f(x) có đồ thị như hình bên. Tìm tất cả các giá trị của tham số m để hàm số y = | f ( x ) + m | có ba điểm cực trị
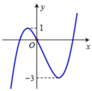
A. m ≤ - 1 hoặc m ≥ 3
B. m ≤ - 2 hoặc m ≥ 3
C. m ≤ - 1 hoặc m ≥ 5
D. 1 ≤ m ≤ 3
Đồ thị hàm số có trục đối xứng là đường thẳng x=3, cắt trục tung tại điểm có tung độ bằng -16 và một trong hai giao điểm với trục hoành có hoành độ là -2. Tìm công thức của hàm số bậc hai.
Gọi công thức của hàm số bậc hai là \(y=ax^2+bx+c\)
Trục đối xứng là x=3 nên \(-\dfrac{b}{2a}=3\)
=>b=-2a
Thay x=0 và y=-16 vào (d), ta được:
\(a\cdot0^2+b\cdot0+c=-16\)
=>c=-16
=>\(y=ax^2+bx-16\)
Thay x=-2 và y=0 vào (d), ta được:
\(a\cdot\left(-2\right)^2+b\left(-2\right)-16=0\)
=>4a-2b-16=0
=>\(4a-2\cdot\left(-2a\right)=16\)
=>8a=16
=>a=2
=>b=-2a=-4
Vậy: Công thức cần tìm là \(y=2x^2-4x-16\)
Cho hàm số bậc 4 có đồ thị như hình vẽ bên. Hỏi đó là đồ thị của hàm số nào?
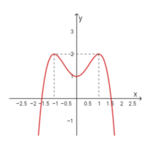
A. y = x 4 - 2 x 2 - 2
B. y = - x 4 + 2 x 2 + 1
C. y = - x 4 - 2 x 2 + 1
D. y = x 4 - 2 x 2 - 1
Đáp án là B.
Từ đồ thị ta thấy a < 0 , mà đồ thị có 3 cực trị nên a . b < 0 ⇒ b > 0
Cho hai hàm số đa thức bậc bốn y = f(x) và y = g(x) có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số y = f(x). Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là -3 và cắt nhau tại hai điểm nữa có hoành độ lần lượt là -1 và 3. Tìm tập hợp tất cả các giá trị thực của tham số m để bất phương trình f x ≥ g x + m nghiệm đúng với mọi x ∈ - 3 ; 3 .
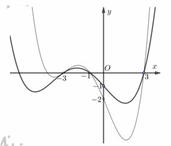
A. - ∞ ; 12 - 8 3 9 .
B. 12 - 10 3 9 ; + ∞ .
C. - ∞ ; 12 - 10 3 9 .
D. 12 - 8 3 9 ; + ∞ .
Cho hàm số bậc ba f(x) và g x = f m x 2 + n x + p m , n , p ∈ có đồ thị như hình dưới (Đường nét liền là đồ thị hàm số f(x) , nét đứt là đồ thị của hàm g(x) đường thẳng x = - 1 2 là trục đối xứng của đồ thị hàm số g(x)
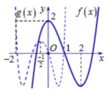
Giá trị của biểu thức P = n + m m + p p + 2 n bằng bao nhiêu?
A.12
B.16
C.24
D.6
Cho f x = x - 1 3 - 3 x + 3 . Đồ thị hình bên là của hàm số có công thức:

A. y = - f x + 1 - 1
B. y = - f x + 1 + 1
C. y = - f x - 1 - 1
D. y = - f x - 1 + 1
Chọn B.
Đáp án A: y = - x 3 - 3 x - 1
Đồ thị hàm số đi qua điểm 0 ; - 1 ⇒ Loại.
Đáp án B: y = - x 3 + 3 x + 1
Đồ thị hàm số đi qua điểm 0 ; 1 ⇒ Đáp án B có thể đúng
Đáp án C: y = - x 3 + 6 x 2 - 15 x + 10 = 0
Đồ thị hàm số đi qua điểm 0 ; 10 ⇒ Loại.
Đáp án D: y = - x 3 + 6 x 2 - 15 x + 12 = 0
Đồ thị hàm số đi qua điểm 0 ; 12 ⇒ Loại.