Để hàm số \(y = \frac{1}{{\sqrt {x - 2} }}\) xác định \( \Leftrightarrow \,\,x - 2 > 0\,\, \Leftrightarrow \,\,x > 2.\)

Vậy tập xác định của hàm số là: \(D = \left( {2; + \infty } \right).\)

Chọn B.

Giao của hai tập hợp là \([ - 2;3] \cap (1; + \infty ) = (1;3]\)

Hiệu của \(B \backslash A \) là \( (1; + \infty ) \backslash [ - 2;3] = (3; + \infty )\)

Phần bù của B trong \(\mathbb{R}\) là: \({C_\mathbb{R}}\;B = \mathbb{R}{\rm{\backslash }}\;(1; + \infty ) = ( - \infty ;1]\)

Ta có: \({x^2} - 6 = 0 \Leftrightarrow x =  \pm \sqrt 6  \in \mathbb{R}\)

Vì \(\sqrt 6  \in \mathbb{R}\) và \( -\sqrt 6  \in \mathbb{R}\) nên \( A = \left\{ { \pm \sqrt 6 } \right\}\)

Nhưng \( \pm \sqrt 6  \notin \mathbb{Z}\) nên không tồn tại \(x \in \mathbb{Z}\) để \({x^2} - 6 = 0\)

Hay \(B = \emptyset \).

Tham khảo:

a) Để xác định tập hợp \(A = (1;3) \cup [ - 2;2]\), ta vẽ sơ đồ sau đây:

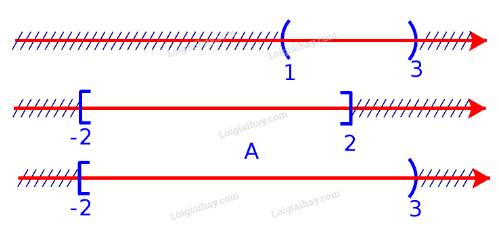
Từ sơ đồ, ta thấy \(A = [ - 2;3)\)

b) Để xác định tập hợp \(B = ( - \infty ;1) \cap [0;\pi ]\), ta vẽ sơ đồ sau đây:

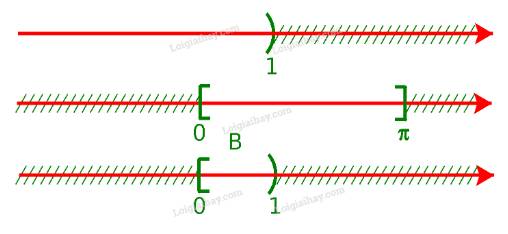
Từ sơ đồ, ta thấy \(B = [0;1)\)

 c) Để xác định tập hợp \(C = [\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\), ta vẽ sơ đồ sau đây:

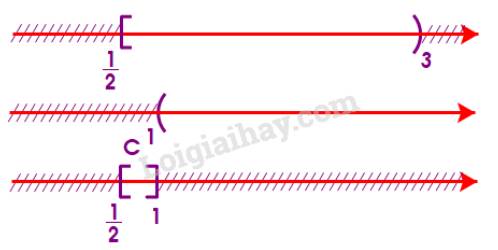
Từ sơ đồ, ta thấy \(C = [\frac{1}{2};1]\)

d) Để xác định tập hợp \(D = {C_\mathbb{R}}[ - 1; + \infty )\), ta vẽ sơ đồ sau đây:

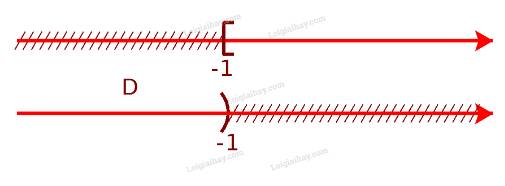
Từ sơ đồ, ta thấy \(D = ( - \infty ; - 1)\)

Tham khảo:

a) Ta có:

Giao của hai tập hợp là \(( - 4;1] \cap [0;3) = \left[ {0;1} \right]\)

b) Ta có:

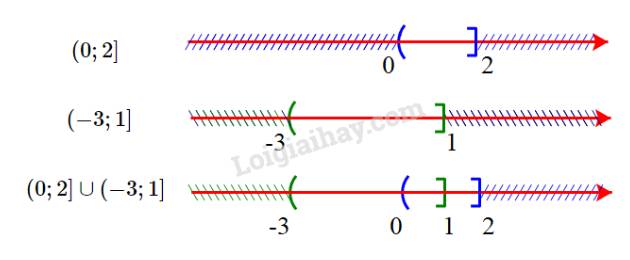
Hợp của hai tập hợp là \((0;2] \cup ( - 3;1] = ( - 3;2]\)

c) Ta có:

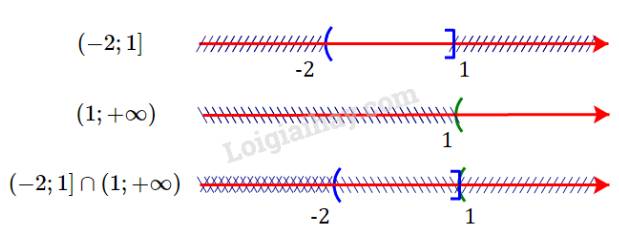
Giao của hai tập hợp là \(( - 2;1] \cap (1;+ \infty )= \emptyset\)

d) Ta có:

Phần bù của tập hợp \(( - \infty ;3]\) trong \(\mathbb{R}\) là \(\mathbb{R}{\rm{\backslash  }}( - \infty ;3] = (3; + \infty )\)

\(C = \{ x \in \mathbb{R}|{x^2} < 0\} \). Tập hợp C không chứa phần tử nào vì bình phương mọi số thực đều không âm.

\(D = \{ a\} ,\) tập hợp D có duy nhất 1 phần tử là a.

\(E = \{ b;c;d\} ,\) tập hợp E có 3 phần tử.

\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\): tập hợp N có vô số phần tử.