Chứng minh rằng hình chiếu song song của một hình thang là một hình thang (H.4.61).
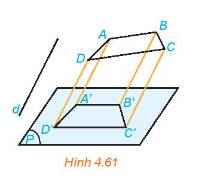
Cho hình thang \(ABCD\) có đáy lớn \(AB\) và \(AB = 2CD\), hình chiếu song song của \(ABCD\) là tứ giác \(A'B'C'D'\). Chứng minh rằng \(A'B'C'D'\) cũng là một hình thang và \(A'B' = 2C'D'\).
\(ABCD\) là hình thang có đáy lớn \(AB \Rightarrow AB\parallel CD\).
Vì hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau, mà hình chiếu song song của \(ABCD\) là tứ giác \(A'B'C'D'\) nên \(A'B'\parallel C'D'\). Vậy \(A'B'C'D'\) cũng là một hình thang.
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau, mà \(AB = 2CD,AB\parallel CD\) và \(A'B'\parallel C'D'\) nên \(A'B' = 2C'D'\).
cho hình thang cân ABCD, AB song song vơi DC, M là trung điểmm của AD, N là trung điểm của BC, H là hình chiếu của A trên DC chứng minh
a)MH song song với CN, MH=CN
b)MN<AC
mọi người trả lời nhanh jup minh minh đang cần
Bài này ko khó đâu. Mình giúp bạn nhé.
a, ABCD là hình thang cân (gt) \(\Rightarrow\hept{\begin{cases}AD=BC\\\widehat{D}=\widehat{C}\end{cases}}\) (t/c hình thang cân)
Tam giác AHD vuông tại H (gt) có HM là đường trung tuyến ứng với cạnh huyền AD nên HM = 1/2 AD
M là trung điểm của AD (gt)\(\Rightarrow MA=MD=\frac{1}{2}AD\)
Do đó: HM = MD \(\Rightarrow\Delta HMD\)cân tại M
\(\Rightarrow\widehat{D}=\widehat{MHD}\) (Tính chất tam giác cân)
Mà \(\widehat{D}=\widehat{C}\left(cmt\right)\Rightarrow\widehat{MHD}=\widehat{C}\Rightarrow MH//CN\) (vì có 2 góc đồng vị bằng nhau.)
Tiếp nhé:
a, N là trung điểm của BC nên CN = 1/2 BC hay CN = 1/2 AD.
Vậy MH = CN (=1/2 AD)
b, Từ kết luận đề bài ý a , ta được MHCN là hình bình hành (có 2 cạnh đối song song và bằng nhau)
\(\Rightarrow MN=HC\)
\(\Delta AHC\) vuông tại H (gt) nên HC<AC (cạnh huyền là cạnh lớn nhất trong tam giác vuông)
Do đó: MN < AC
Chúc bạn học tốt.
Chứng minh định lý: "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng:
a) ΔBDE là tam giác cân.
b) ΔACD = ΔBDC
c) Hình thang ABCD là hình thang cân.
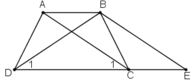
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó ΔBDE cân

Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Chứng minh định lý: "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng: a) ΔBDE là tam giác cân. b) ΔACD = ΔBDC c) Hình thang ABCD là hình thang cân.
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó \(\Delta BDE\) cân
b ) Ta có : AC // BE
\(\Rightarrow\widehat{C}_1=\widehat{E}\) ( 3 )
Tam giác BDE cân tại B ( câu a ) nên \(\widehat{D}_1=\widehat{E}\) ( 4 )
Từ (3 ) và ( 4 ) \(\Rightarrow\widehat{C}_1=\widehat{D}_1\)
Xét \(\Delta ACD\) và \(\Delta BCD\) có AC = CD ( gt )
\(\widehat{C}_1=\widehat{D}_1\left(cmt\right)\)
CD là cạnh chung
Nên \(\Delta ACD=\Delta BCD\left(c.g.c\right)\)
c ) Vì \(\Delta ACD=\Delta BCD\) ( câu b ) \(\Rightarrow\widehat{ADC}=\widehat{BCD}\)
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Chúc bạn học tốt !!!
1) Chứng minh định lí “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau : Cho hình thang ABCD(AB//CD)ABCD(AB//CD) có AC=BDAC=BD. Qua BB kẻ đường thẳng song song với ACAC, cắt đường thẳng DCDC tại EE. Chứng minh rằng:
a) BDEBDE là tam giác cân.
b) △ACD=△BDC.△ACD=△BDC.
c) Hình thang ABCDABCD là hình thang cân.
chúc hok tốt , k nha! sai cũng k
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.
a) Tìm các hình thang trong hình vẽ
b)chứng minh rằng hình thang BDEC là một cạnh đáy bằng tổng hai cạnh bên
b: Xét ΔDBI có
\(\widehat{DBI}=\widehat{DIB}\)
nên ΔDBI cân tại D
Xét ΔEIC có \(\widehat{EIC}=\widehat{ECI}\)
nên ΔEIC cân tại E
Ta có: DE=DI+IE
nên DE=DB+EC
Vậy: BDEC là hình thang có một cạnh đáy bằng tổng hai cạnh bên
cho hình thang ABCD (AB/CD) có AC=BD . Qua B kẻ đường thẳng song song với AC , cắt đường thẳng DC tại E :
a, chứng minh rằng tam giác BDE cân
b, chứng minh tam giác ACD= tam giác BDC
c, chúng minh hình thang ABCD là hình thang cân
a: Xét tứ giác ABEC có
AB//CE
AC//BE
Do đó: ABEC là hình bình hành
Suy ra: AC=BE
mà AC=BD
nên BE=BD
Xét ΔBDE có BE=BD
nên ΔBDE cân tại B
b: Xét ΔACD và ΔBDC có
AC=BD
AD=BC
CD chung
Do đó: ΔACD=ΔBDC
c: Hình thang ABCD có AC=BD
nên ABCD là hình thang cân
cho hình thang ABCD có AC=BD Qua B kẻ đưởng thẳng song song AC cát DC tại E. Chứng minh rằng :
a. tam giấc ABE cân
b. ΔACD =ΔBDC
c. Hình thang ABCD là hình thang cân
c: hình thang ABCD có AC=BD
nên ABCD là hình thang cân
cho hình thang abcd có ab song song cd m thuộc hình thang vẽ các hình bình hành abcd e f chứng minh rằng ef song song cd ab = ab + cd
Cho tam giác ABC, các tia phân giác của góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt cạnh AB và AC tại D và E.
a) Vẽ hình và tìm các hình thang trong hình vẽ.
b) Chứng minh rằng hình thang BCED có một cạnh đáy bằng tổng hai cạnh bê
\(a,\) Các hình thang \(BDEC;BDIC;BIEC\)
\(b,DE//BC.nên.\widehat{B_1}=\widehat{I_1}\left(so.le.trong\right)\)
Mà \(\widehat{B_1}=\widehat{B_2}\left(t/c.phân.giác\right)\) nên \(\widehat{B_2}=\widehat{I_1}\Rightarrow\Delta DIB\) cân tại D
\(\Rightarrow DI=DB\left(1\right)\)
\(DE//BC.nên.\widehat{C_1}=\widehat{I_2}\left(so.le.trong\right)\)
Mà \(\widehat{C_1}=\widehat{C_2}\left(t/c.phân.giác\right)\) nên \(\widehat{C_2}=\widehat{I_2}\Rightarrow\Delta IEC\) cân tại E
\(\Rightarrow EI=EC\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow DI+IE=BD+EC\\ \Rightarrow DE=BD+CE\left(Đpcm\right)\)