Trong Ví dụ 4, xác định giao tuyến của hai mặt phẳng (SAC) và (SBD).

Những câu hỏi liên quan
Trong Ví dụ 4, hãy xác định giao tuyến của hai mặt phẳng (SAD) và (SBC)
Hai mp(SAD) và (SBC) có điểm chung S và chứa hai đường thẳng song song AD và BC.
Do đó, giao tuyến của hai mp(SAD) và (SBC) là đường thẳng n đi qua S song cong với AD và BC.
Đúng 0
Bình luận (0)
Trong Ví dụ 3, hãy xác định giao tuyến của hai mặt phẳng (SBM) và (SCN).
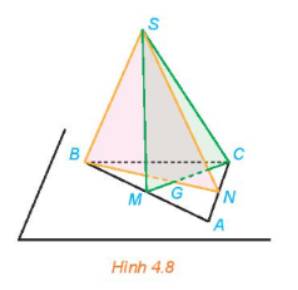
Vì A là giao điểm của BM và CN nên A nằm trên cả hai mặt phẳng (SBM) và (SCN).
Ta có: S, A là hai điểm chung của hai mặt phẳng (SBM) và (SCN) nên giao tuyến của hai mặt phẳng này là đường SA.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD và AB < CD. Xác định giao tuyến của hai mặt phẳng sau:
a) (SAD) và (SBC)
b) (SAB) và (SCD)
c) (SAC) và (SBD)
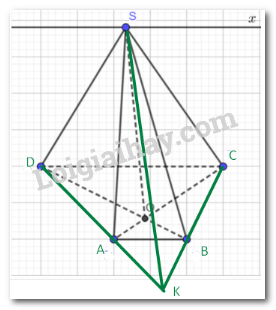
a) Gọi giao điểm của AD và BC là K.
Ta có: SK cùng thuộc mp(SAD) và (SBC).
Vậy SK là giao tuyến của (SAD) và (DBC).
b) (SAB) và (SCD) có AB // CD và S chung nên giao tuyến là dường thẳng Sx đi qua x và song song với AB và CD.
c) Gọi O là giao điểm của AC và BD suy ra O thuộc giao tuyến của (SAC) và (SBC)
Suy ra SO là giao tuyến của (SAC) và (SBD).
Đúng 0
Bình luận (0)
Trong Ví dụ 3, hãy xác định giao tuyến của mặt phẳng (EMQ) và mặt phẳng (ABCD).
Ta có (MNPQ) // (ABCD) (chứng minh ở Ví dụ 2)
Vì vậy giao tuyến của (EMQ) với hai mặt phẳng (MNPQ) và (ABCD) song song với nhau
Trong mặt phẳng (EMQ), qua E vẽ đường thẳng ET // MQ (T thuộc CD)
Như vậy, đường thẳng ET là giao tuyến của (EMQ) và (ABCD).
Đúng 0
Bình luận (0)
Trong Ví dụ 4, gọi (Q) là mặt phẳng qua E và song song với hai đường thẳng AB, AD. Xác định giao tuyến của (Q) với các mặt của tứ diện.
Mặt phẳng (ABC) chứa đường thẳng AB song song với (Q) nên mp(ABC) cắt mp(Q) theo giao tuyến song song với AB. Vẽ EF // AB (F thuộc BC) thì EF là giao tuyến của (Q) và (ABC).
Hai mặt phẳng (ACD) và (ABD) cùng chứa đường thẳng AD song song với (Q) nên chúng cắt mặt phẳng (Q) theo giao tuyến song song với với AD. Vẽ EK song song với AD (K thuộc CD) thì EK, FK lần lượt là giao tuyến của mp(Q) với hai mp(ACD) và (BCD).
Đúng 0
Bình luận (0)
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Giả sử (α) là mặt phẳng đi qua A và vuông góc với cạnh SC, (α) cắt SC tại I.a) Xác định giao điểm K của SO với mặt phẳng (α).b) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) và BD // (α).c) Xác định giao tuyến d của mặt phẳng (SBD) và mặt phẳng (α). Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng (α).
Đọc tiếp
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Giả sử (α) là mặt phẳng đi qua A và vuông góc với cạnh SC, (α) cắt SC tại I.
a) Xác định giao điểm K của SO với mặt phẳng (α).
b) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) và BD // (α).
c) Xác định giao tuyến d của mặt phẳng (SBD) và mặt phẳng (α). Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng (α).
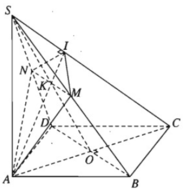
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).
b) Ta có 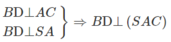
⇒ BD ⊥ SC
Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).
Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)
Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).
Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.
Đúng 0
Bình luận (0)
cho hình chóp s.abcd có đáy là hình bình hành. Gọi M,N lần lượt là trung điểm của các cạng SA,SC, và G là trọng tâm của △ABC
a) tìm giao tuyến của hai mặt phẳng (SAC) và (SBD)
b) tìm giao điểm BC và mặt phẳng (GMN)
c) xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (GMN)
a/
Ta có
\(S\in\left(SAC\right);S\in\left(SBD\right)\)
Trong mp (ABCD) gọi O là giao của AC và BD
\(O\in AC\Rightarrow O\in\left(SAC\right);O\in BD\Rightarrow O\in\left(SBD\right)\)
\(\Rightarrow SO\in\left(SAC\right)\) và \(SO\in\left(SBD\right)\) => SO là giao tuyến của (SAC) và (SBD)
b/
Trong mp (ABCD) Từ G dựng đường thẳng // AC cắt BC tại K
Xét tg SAC có
SM=AM (gt); SN=CN (gt) => MN là đường trung bình của tg SAC
=> MN//AC
Mà GM//AC
=> MN//GK mà \(G\in\left(GMN\right)\Rightarrow GK\in\left(GMN\right)\) (Từ 1 điểm trong mặt phẳng chỉ dựng được duy nhất 1 đường thẳng thuộc mặt phẳng đó và // với 1 đường thẳng cho trươc thuộc mặt phẳng)
\(\Rightarrow K\in\left(GMN\right);K\in BC\) => K llaf giao của BC với (GMN)
c/
Ta có
\(KN\in\left(GMN\right);KN\in\left(SBC\right)\) => KN là giao tuyến của (GMN) với (SBC)
Trong (ABCD) KG cắt AB tại H
\(KG\in\left(GMN\right)\Rightarrow KH\in\left(GMN\right)\)
\(KG\in\left(ABCD\right)\Rightarrow KH\in\left(ABCD\right)\)
=> KH là giao tuyến của (GMN) với (ABCD)
Ta có
\(HM\in\left(SAB\right);HM\in\left(GMN\right)\) => HM là giao tuyến của (GMN) với (SAB)
Trong mp(SAC) gọi P là giao của SO với MN
\(P\in MN\Rightarrow P\in\left(GMN\right)\)
Trong mp(SBD) Nối G với P cắt SD tại Q
\(\Rightarrow GP\in\left(GMN\right)\Rightarrow Q\in GMN\)
\(\Rightarrow MQ\in\left(GMN\right)\) mà \(MQ\in\left(SAD\right)\) => MQ là giao tuyến của (GMN) với (SAD)
Ta có
\(NQ\in\left(GMN\right);NQ\in\left(SCD\right)\) => NQ là giao tuyến của (GMN) với (SCD)
=> thiết diện của hình chóp bị cắt bởi (GMN) là đa giác HMQNK
Đúng 1
Bình luận (0)
Trong Ví dụ 4, vẽ một đường thẳng c cắt cả hai đường thẳng a và b. Xác định giao tuyến của hai mặt phẳng: mp (S, a) và mp (S, c); mp (S, b) và mp (S, c).
Đường thẳng c cắt a, b lần lượng tại A và B.
Giao tuyến của mp(S,a) và mp(S,c) là SA.
Giao tuyến của mp(S,b) và mp(S,c) là SB.
Đúng 0
Bình luận (0)
cho hình chóp S.ABCD, đáy ABCD là vuông tâm I. Gọi M,N lần lượt là trung điểm SB,SC
a) tìm giao tuyến của hai mặt phẳng (SBD) và (SAC)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
d) tìm giao tuyến của 2 mặt phẳng (MNA) và (ABCD)
a: \(I\in BD\subset\left(SBD\right)\)
\(I\in AC\subset\left(SAC\right)\)
Do đó: \(I\in\left(SBD\right)\cap\left(SAC\right)\)
=>\(\left(SBD\right)\cap\left(SAC\right)=SI\)
b: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
c: AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: (SAD) giao (SBC)=mn, mn đi qua S và mn//AD//BC
Đúng 4
Bình luận (0)















