Điểm thi môn Toán (thang điểm 100, điểm được làm tròn đến 1) của 60 thí sinh được cho trong bảng sau:

a) Hiệu chỉnh để thu được mẫu số liệu ghép nhóm dạng Bảng 3.2.
b) Tìm các tứ phân vị và giải thích ý nghĩa của chúng.
Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau:

a) Tìm tứ phân vị của dãy số liệu trên.
b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
c) Hãy ước lượng tứ phân vị của số liệu từ bảng tần số ghép nhóm trên.
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right) = \frac{1}{2}\left( {11 + 11} \right) = 11\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) = \frac{1}{2}\left( {14 + 14} \right) = 14\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right) = \frac{1}{2}\left( {21 + 22} \right) = 21,5\)
b)

c) Do số trận đấu là số nguyên nên ta hiệu chỉnh như sau:

Tổng trận đấu là: \(n = 4 + 8 + 2 + 6 = 20\).
Gọi \({x_1};{x_2};...;{x_{20}}\) là điểm số của các trận đấu được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_4} \in \begin{array}{*{20}{c}}{\left[ {5,5;10,5} \right)}\end{array};{x_5},...,{x_{12}} \in \begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array};{x_{13}},{x_{14}} \in \begin{array}{*{20}{c}}{\left[ {15,5;20,5} \right)}\end{array};{x_{15}},...,{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right)\)
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_{10}},{x_{11}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}.\left( {15,5 - 10,5} \right) = 14,25\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_5},{x_6} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{4} - 4}}{8}.\left( {15,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 6;C = 4 + 8 + 2 = 14;{u_j} = 20,5;{u_{j + 1}} = 25,5\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 20,5 + \frac{{\frac{{3.20}}{4} - 14}}{6}.\left( {25,5 - 20,5} \right) \approx 21,3\)
Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau:
Hãy ước lượng số trung bình, tứ phân vị và mốt của mẫu số liệu ghép nhóm trên.
Tổng số học sinh: \(n = 8 + 10 + 16 + 24 + 13 + 7 + 4 = 82\)
• Điểm trung bình môn Toán của các học sinh lớp 11 trên là:
\(\bar x = \frac{{8.6,75 + 10.7,25 + 16.7,75 + 24.8,25 + 13.8,75 + 7.9,25 + 4.9,75}}{{82}} = 8,12\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {8;8,5} \right)\).
Do đó: \({u_m} = 8;{n_{m - 1}} = 16;{n_m} = 24;{n_{m + 1}} = 13;{u_{m + 1}} - {u_m} = 8,5 - 8 = 0,5\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{24 - 16}}{{\left( {24 - 16} \right) + \left( {24 - 13} \right)}}.0,5 \approx 8,21\)
• Gọi \({x_1};{x_2};...;{x_{82}}\) là điểm của các học sinh lớp 11 được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_8} \in \begin{array}{*{20}{c}}{\left[ {6,5;7} \right)}\end{array};{x_9},...,{x_{18}} \in \begin{array}{*{20}{c}}{\left[ {7;7,5} \right)}\end{array};{x_{19}},...,{x_{34}} \in \begin{array}{*{20}{c}}{\left[ {7,5;8} \right)}\end{array};{x_{35}},...,{x_{58}} \in \begin{array}{*{20}{c}}{\left[ {8;8,5} \right)}\end{array};\\{x_{59}},...,{x_{71}} \in \begin{array}{*{20}{c}}{\left[ {8,5;9} \right)}\end{array};{x_{72}},...,{x_{78}} \in \begin{array}{*{20}{c}}{\left[ {9;9,5} \right)}\end{array};{x_{79}},...,{x_{82}} \in \begin{array}{*{20}{c}}{\left[ {9,5;10} \right)}\end{array}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{41}} + {x_{42}}} \right)\)
Ta có: \(n = 82;{n_m} = 24;C = 8 + 10 + 16 = 34;{u_m} = 8;{u_{m + 1}} = 8,5\)
Do \({x_{41}},{x_{42}} \in \begin{array}{*{20}{l}}{\left[ {8;8,5} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{\frac{{82}}{2} - 34}}{{24}}.\left( {8,5 - 8} \right) \approx 8,15\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_{21}}\).
Ta có: \(n = 82;{n_m} = 16;C = 8 + 10 = 18;{u_m} = 7,5;{u_{m + 1}} = 8\)
Do \({x_{21}} \in \begin{array}{*{20}{l}}{\left[ {7,5;8} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 7,5 + \frac{{\frac{{82}}{4} - 18}}{{16}}.\left( {8 - 7,5} \right) \approx 7,58\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{62}}\).
Ta có: \(n = 82;{n_j} = 13;C = 8 + 10 + 16 + 24 = 58;{u_j} = 8,5;{u_{j + 1}} = 9\)
Do \({x_{62}} \in \begin{array}{*{20}{l}}{\left[ {8,5;9} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 8,5 + \frac{{\frac{{3.82}}{4} - 58}}{{13}}.\left( {9 - 8,5} \right) \approx 8,63\)
Để khảo sát kết quả kì thi thử THPT môn toán của trường A; người điều tra chọn một mẫu gồm 100 học sinh tham gia kì thi tuyển sinh đó. Điểm môn Toán được cho ở bảng phân bố tần số sau đây.
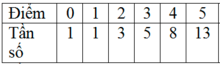

Tìm số trung vị
A. 6, 5
B. 7,5
C. 6
D. 5,5
Chọn A.
Do kích thước mẫu N = 100 là một số chẵn nên số trung vị là trung bình cộng của 2 giá trị đứng thứ 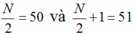
do đó 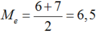
Với mẫu số liệu ghép nhóm cho trong HĐ2, hãy cho biết tứ phân vị nhất \({Q_1}\) và tứ phân vị thứ ba \({Q_3}\) thuộc nhóm nào.
Cho mẫu số liệu ghép nhóm như Bảng 3.2
Cỡ mẫu là: \(n = 21\).
Suy ra tứ phân vị thứ nhất \({Q_1}\)là \(\frac{{{x_5} + {x_6}}}{2}\). Do \({x_5};{x_6}\) đều thuộc nhóm [5;10) nên từ phân vị thứ nhất thuộc nhóm [5;10).
Tứ phân vị thứ ba \({Q_3}\) là \(\frac{{{x_{16}} + {x_{17}}}}{2}\) . Do \({x_{16}};\;{x_{17}}\)đều thuộc nhóm [10; 15) nên tứ phân vị thứ ba thuộc nhóm [10; 15).
Số liệu thống kê điểm kiểm tra môn Toán của học sinh lớp 10A được cho trong bảng sau:
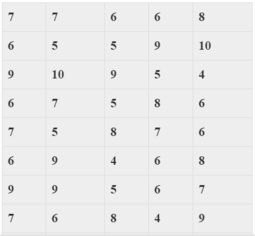

Đơn vị điều tra và kích thước mẫu của bảng số liệu trên là:
A. Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A. Kích thước mẫu của số liệu: 44
B. Đơn vị điều tra: Điểm trung bình môn Toán của lớp 10A. Kích thước mẫu của số liệu: 45
C. Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A. Kích thước mẫu của số liệu: 45
D. Đơn vị điều tra: Điểm trung bình môn Toán của lớp 10A. Kích thước mẫu của số liệu: 44
Chọn A.
Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A
Liệt kê số điểm của 44 học sinh lớp 10A nên kích thước mẫu của số liệu là 44.
Để khảo sát kết quả kì thi thử THPT môn toán của trường A; người điều tra chọn một mẫu gồm 100 học sinh tham gia kì thi tuyển sinh đó. Điểm môn Toán được cho ở bảng phân bố tần số sau đây.
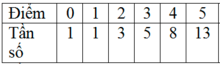
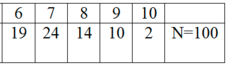
Tìm mốt
A. 24
B. 7
C. 8
D. 19
Chọn B.
Nhìn vào bảng tần số ta thấy giá trị 7 có tần số lớn nhất nên M0= 7.
Điểm kiểm tra môn toán của 20 học sinh được liệt kê trong bảng sau:
8 | 6 | 9 | 7 | 7 | 9 | 10 | 6 | 5 | 4 |
7 | 10 | 8 | 7 | 7 | 9 | 9 | 7 | 8 | 8 |
Sử dụng bảng số liệu trên để trả lời các câu 1 đến câu 6:
Câu 1: Tổng các giá trị của dấu hiệu là:
A. 151 B. 165 C. 153 D. 20
Câu 2: Số N bằng bao nhiêu?
A. 6 B. 8 C. 10 D. 20
Câu 3: Số các giá trị khác nhau của dấu hiệu là:
A. 20 B. 8 C. 10 D. 7
Câu 4: Tần số của học sinh có điểm 10 là:
A. 4 B. 5 C. 3 D. 2
Câu 5: Mốt của dấu hiệu là:
A. 8 B. 5 C. 7 D. 6
Câu 6: Số trung bình cộng là:
A. 7,65 B. 8,25 C. 7,82 D. 7,55
Câu 7: Biểu thức đại số biểu thị cho bình phương của tổng x và y là:
A. x + (-y) B. x + y C. (x + y)2 D. x2 + y2.
Câu 8: Giá trị của biểu thức -x5y + x2y + x5y tại x = -1; y = 1 là:
A. 1 B. -2 C. -1 D. 2
Câu 9: Số giá trị nguyên của x để biểu thức A = ( x có giá trị nguyên
A. 4 B. 2 C. 5 D. 7
Câu 10: Trong các biểu thức sau, biểu thức nào không phải là một đơn thức?
A. x + y B. (1+ )xyz2 C. 2x D. 0
Câu 11: Bậc của đơn thức – x2y2(-xy4) là:
A. 8 B. 6 C. 9 D. 4
Câu 12: Trong các đơn thức sau: – 2xy5 ; 7 ; - 3x5y ; 6xy5; x5y; 0. Số các cặp đơn thức đồng dạng là:
A. 1 B. 2 C. 3 D. 4
Câu 13: Kết quả sau khi rút gọn biểu thức là:
A. -6x4y3 B. -6x4y4 C. 6x4y4 D. 6x4y3
Câu 14 : Giá trị của biểu thức khi 5x=3y bằng
A.
B. -8
C. 8
D. -
Câu 15: Tổng ba góc của một tam giác bằng
A. 1800 B. 3600 C. 900 D. 450
Câu 16: Góc ngoài của tam giác bằng:
A. tổng ba góc trong của tam giác.
B. tổng hai góc trong không kề với nó.
C. tổng hai góc trong.
D. góc kề với nó.
Câu 17: Cho tam giác ABC có . Tìm số đo của
A. 500 B. 900 C. 1100 D. 700
Câu 18: Cho MNP = DEF. Suy ra:
A. . B. C. . D.
Câu 19: Cho có . Các đường phân giác của góc B và góc C cắt nhau tại I. Số đo góc BIC bằng:
A. 1500 B. 300 C. 1200 D. 600
Câu 20: Tam giác ABC vuông tại B suy ra:
A. AC2 = AB2 + BC2 B. AC2 = AB2 - BC2
C. BC2 = AB2 + AC2 D. AB2 = BC2 + AC2
Câu 21: Tam giác ABC có BC = 5cm; AC = 12cm; AB = 13cm. Tam giác ABC vuông tại đâu?
A. Tại B B. Tại C
C. Tại A D. Không phải là tam giác vuông
Câu 22: Cho ABC có = 900 ; AB = 4,5 cm ; BC = 7,5 cm. Độ dài cạnh AC là:
A. 6,5 cm B. 5,5 cm C. 6 cm D. 6,2 cm
Câu 23: Tam giác nào là tam giác vuông trong các tam giác có độ dài các cạnh là:
A. 3cm, 4dm, 5cm. B. 5cm, 14cm, 12cm.
C. 5cm, 5cm, 8cm. D. 9cm, 15cm, 12cm.
Câu 24: Cho ABC có AB = AC và = 600, khi đó tam giác ABC là:
A. Tam giác vuông B. Tam giác cân
C. Tam giác đều D. Tam giác vuông cân
Câu 25: Nếu A là góc ở đáy của một tam giác cân thì:
A. ∠A ≤ 900 B. ∠A > 900 C. ∠A < 900 D. ∠A = 900
Ai giúp mình với ạ, câu 1 đến câu 12 mình làm được rồi, còn lại giúp mình với!
Kết quả kì thi trắc nghiệm môn Toán với thang điểm 100 của 32 học sinh được cho trong mẫu số liệu sau:
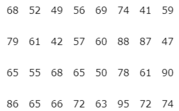
Các số liệu trên được phân thành 6 lớp:
L 1 = [ 40 ; 50 ) ; |
L 2 = [ 50 ; 60 ) ; |
L 3 = [ 60 ; 70 ) ; |
L 4 = [ 70 ; 80 ) ; |
L 5 = [ 80 ; 90 ) ; |
L 6 = [ 90 ; 100 ) . |
Có bao nhiêu học sinh có số điểm trong nửa khoảng [50;80) ?
A. 23
B. 24
C. 25
D. 26
Ta lập bảng phân bố tần số ghép lớp:
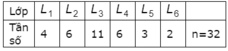
Số học sinh có số điểm trong nửa khoảng [50;80) là 6 + 11 + 6 = 23.
Điểm Toán và điểm Tiếng Anh của 11 học sinh lớp 10 được cho trong bảng sau:

Hãy so sánh mức độ học đều của học sinh trong môn Tiếng Anh và môn Toán thông qua các số đặc trưng: khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn.
Sắp xếp lại:
5 | 31 | 37 | 43 | 43 | 57 | 62 | 63 | 78 | 80 | 91 |
Khoảng biến thiên R=91-5=86
Ta có: \({Q_2} = 57,{Q_1} = 37,{Q_3} = 78\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 78 - 37 = 41\)
Số trung bình \(\overline X \approx 53,64\)
Ta có bảng sau:
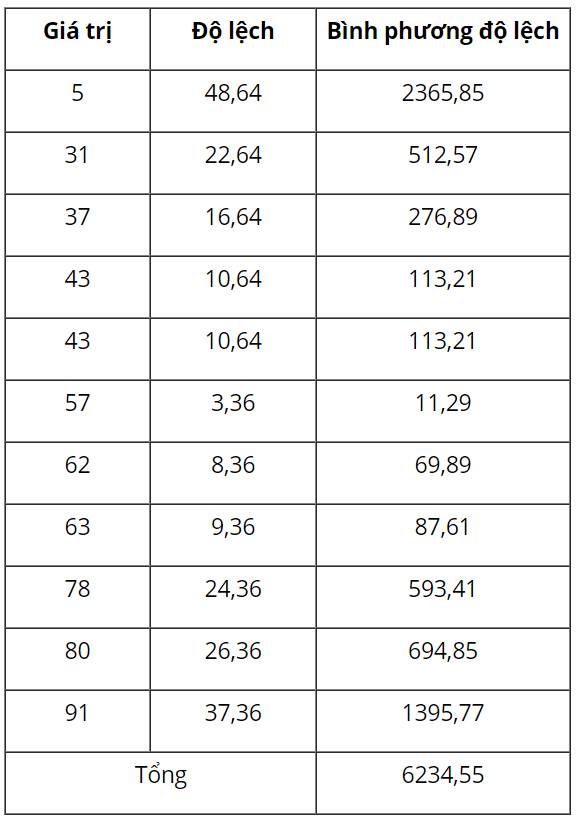
Độ lệch chuẩn là 79
Môn Tiếng Anh:
Sắp xếp lại:
37 | 41 | 49 | 55 | 57 | 62 | 64 | 65 | 65 | 70 | 73 |
Khoảng biến thiên R=73-37=36
Ta có: \({Q_2} = 62,{Q_1} = 49,{Q_3} = 65\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 65 - 49 = 16\)
Số trung bình \(\overline X = 58\)
Ta có bảng sau:
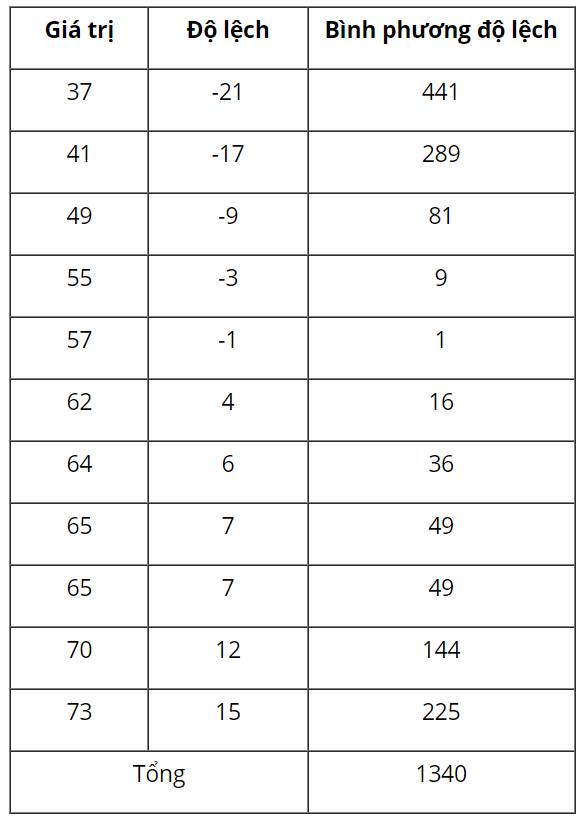
Độ lệch chuẩn là 36,6
Từ các số trên ta thấy mức độ học tập môn Tiếng Anh không đều bằng môn Toán.Độ lệch chuẩn là 36,6