Tuổi thọ (năm) của 50 bình ắc quy ô tô được cho như sau:

a) Xác định mốt và giải thích ý nghĩa.
b) Tính tuổi thọ trung bình của 50 bình ắc quy ô tô này.
Nghiên cứu "tuổi thọ" của một loại bóng đèn, người ta đã chọn tùy ý 50 bóng và bật sáng liên tục cho tới lúc chúng tự tắt. "Tuổi thọ" của các bóng (tính theo giờ) được ghi lại ở bảng 23 (làm tròn đến hàng chục):
| Tuổi thọ (x) | 1150 | 1160 | 1170 | 1180 | 1190 | |
| Số bóng đèn tương ứng (n) | 5 | 8 | 12 | 18 | 7 | N = 50 |
Tính số trung bình cộng.
Số trung bình cộng của tuổi thọ các bóng đèn đó là:
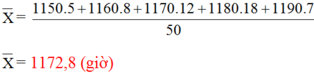
Quan sát biểu đồ sau và trả lời các câu hỏi:

a) Tuổi thọ trung bình của người Việt Nam năm 1989 là bao nhiêu?
b) Tuổi thọ trung bình của người Việt Nam năm 2019 là bao nhiêu?
c) Từ năm 1989 đến năm 2019, tuổi thọ trung bình của người Việt Nam đã tăng bao nhiêu tuổi?
a) Tuổi thọ trung bình của người Việt Nam năm 1989 là 65 tuổi
b) Tuổi thọ trung bình của người Việt Nam năm 2019 là 74 tuổi
c) Từ năm 1989 đến năm 2019, tuổi thọ trung bình của người Việt Nam đã tăng lên là: 74 - 65 = 9 (tuổi)
Nghiên cứu "tuổi thọ" của một loại bóng đèn, người ta đã chọn tùy ý 50 bóng và bật sáng liên tục cho tới lúc chúng tự tắt. "Tuổi thọ" của các bóng (tính theo giờ) được ghi lại ở bảng 23 (làm tròn đến hàng chục):
| Tuổi thọ (x) | 1150 | 1160 | 1170 | 1180 | 1190 | |
| Số bóng đèn tương ứng (n) | 5 | 8 | 12 | 18 | 7 | N = 50 |
Tìm mốt của dấu hiệu.
Tìm mốt của dấu hiệu:
Ta biết mốt là giá trị có tần số lớn nhất trong bảng. Mà tần số lớn nhất trong bảng là 18.
Vậy mốt của dấu hiệu bằng 1180 hay Mo = 1180.
Để nghiên cứu "tuổi thọ" của một loại bóng đèn, người ta đã chọn tùy ý 50 bóng và bật sáng liên tục cho tới lúc chúng tự tắt. "Tuổi thọ" của các bóng (tính theo giờ) được ghi lại ở bảng 23 (làm tròn đến hàng chục) "

a) Dấu hiệu cần tìm hiểu ở đây là gì và số các giá trị là bao nhiêu ?
b) Tính số trung bình cộng ?
c) Tìm mốt của dấu hiệu ?
a) - Dấu hiệu: Thời gian cháy sáng liên tục cho tới lúc tự tắt của bóng đèn tức "tuổi thọ" của một loại bóng đèn.
- Số các giá trị N = 50
b) Số trung bình cộng của tuổi thọ các bóng đèn đó là:
c) Tìm mốt của dấu hiệu:
Ta biết mốt là giá trị có tần số lớn nhất trong bảng. Mà tần số lớn nhất trong bảng là 18.
Vậy mốt của dấu hiệu bằng 1180 hay Mo = 1180.
a) - Dấu hiệu: Thời gian cháy sáng liên tục cho tới lúc tự tắt của bóng đèn tức "tuổi thọ" của một loại bóng đèn.
- Số các giá trị N = 50
b) Số trung bình cộng của tuổi thọ các bóng đèn đó là:
c) Tìm mốt của dấu hiệu:
Ta biết mốt là giá trị có tần số lớn nhất trong bảng. Mà tần số lớn nhất trong bảng là 18.
Vậy mốt của dấu hiệu bằng 1180 hay Mo = 1180
Người ta ghi lại tuổi thọ của một số con ong và cho kết quả như sau:
Tuổi thọ (ngày) | [0; 20) | [20; 40) | [40; 60) | [60; 80) | [80; 100) |
Số lượng | 5 | 12 | 23 | 31 | 29 |
Tìm mốt của mẫu số liệu. Giải thích ý nghĩa của giá trị nhận được.
Tần số lớn nhất là 31
=>Nhóm chứa mốt là [60;80)
j=4
a4=60
m4=31; m3=23; m5=29; h=20
Do đó, ta có:
\(M_0=60+\dfrac{31-23}{\left(31-23\right)+\left(31-29\right)}\cdot20=76\)
=>Đa số các con ong có tuổi thọ là 76 ngày
Người ta ghi lại tuổi thọ của một số con ong cho kết quả như sau:

Tìm mốt của mẫu số liệu. Giải thích ý nghĩa của giá trị nhận được.
Tần số lớn nhất là 31 nên nhóm chứa mốt là \(\left[ {60;80} \right).\;\)Ta có:
\(j = 4;\;\;{a_4} = 60;\;\;{m_4} = 31;\;\;{m_3} = 23;\;\;{m_5} = 29;\;\;h = 20\). Do đó,
\({M_0} = 60 + \frac{{31 - 23}}{{\left( {31 - 23} \right) + \left( {31 - 29} \right)}} \times 20 = 76\).
Ý nghĩa: Đa số các con ong có tuổi thọ là 76 ngày.
67 tuổi (năm 2005) là tuổi thọ trung bình của
A. các nước phát triển
B. các nước đang phát triển
C. các nước châu Phi
D. thế giới
76 tuổi (năm 2005) là tuổi thọ trung bình của
A. thế giới
B. các nước châu Phi
C. các nước phát triển
D. các nước đang phát triển
52 tuổi (năm 2005) là tuổi thọ trung bình của
A. thế giới
B. châu Phi.
C. nhóm nước phát triển
D. nhóm nước đang phát triển