Cho hình vuông ABCD có cạnh bằng 2 căn5. Gọi M và N lần lượt là trung điểm của AD, và I là giao của AN, BM
a) CMR: AN vuông góc
b) Tính AI, MI
c) Tính diện tích BINC
Cho hình vuông ABCD cạnh a .Gọi M, N, K lần lượt là trung điểm của AD, AB, BC
a)cmr TỨ GIÁC DMBK là hình bình hành
b)Gọi I, J lần lượt là giao điểm của CN vs BM và DK.cmr J LÀ TRUNG ĐIỂM CỦA CI
C)cm TAM GIÁC abm = TAM GIÁC BCN từ đó suy ra BM VUÔNG GÓC VS cb
d)Tính DI theo a
Cho hình vuông ABCD có độ dài cạnh bằng a. Trên cạnh AD và CD lần lượt lấy các điểm M và N saoo cho góc MBN bằng 45 độ, BM và BN cắt AC theo thứ tự tại E và F.
a) Chứng minh MF vuông góc với BN.
b) Gọi H là giao điểm của MF với NE và I là giao điểm của BH với MN. Tính độ dài đoạn BI theo a.
c) Tìm vị trí của M và N sao cho diện tích tam giác MDN lớn nhất.
Cho hình vuông ABCD cạnh có độ dài bằng a. Trên cạnh AD lấy điểm M và cạnh CD lấy điểm N sao cho góc MBN = 45°. Gọi E và F lần lượt là giao điểm của BM, BN với AC. a/ Chứng minh: Tứ giác BENC nội tiếp, từ đó suy ra NE vuông góc với BM b/ Gọi I là giao điểm của NE và MF. Chứng minh: BI vuông góc với MN. c/ Tìm vị trí của M và N để diện tích tam giác MDN lớn nhất. Tính diện tích lớn nhất đó theo a.
a.
DO ABCD là hình vuông \(\Rightarrow\widehat{ACD}=45^0\)
\(\Rightarrow\widehat{ACD}=\widehat{EBN}\)
Mà \(\widehat{ACD}\) và \(\widehat{EBN}\) cùng chắn EN
\(\Rightarrow\) Tứ giác BENC nội tiếp
\(\Rightarrow\widehat{BEN}+\widehat{BCN}=180^0\)
\(\Rightarrow\widehat{BEN}=180^0-\widehat{BCN}=180^0-90^0=90^0\)
\(\Rightarrow NE\perp BM\) tại E
b.
Tương tự ta có tứ giác ABFM nội tiếp (\(\widehat{MAF}=\widehat{MBF}=45^0\) cùng chắn MF)
\(\Rightarrow\widehat{BFM}+\widehat{BAM}=180^0\)
\(\Rightarrow\widehat{BFM}=90^0\Rightarrow MF\perp BN\)
\(\Rightarrow I\) là trực tâm của tam giác BMN
\(\Rightarrow BI\perp MN\)
c.
Gọi H là giao điểm BI và MN
Do E và F cùng nhìn MN dưới 1 góc vuông
\(\Rightarrow\) Tứ giác EFMN nội tiếp
\(\Rightarrow\widehat{EMN}+\widehat{EFN}=180^0\)
Mà \(\widehat{EFN}+\widehat{EFB}=180^0\)
\(\Rightarrow\widehat{EMN}=\widehat{EFB}\)
Lại có tứ giác ABFM nội tiếp (A và F cùng nhìn BM dưới 1 góc vuông)
\(\Rightarrow\widehat{EFB}=\widehat{AMB}\) (cùng chắn AB)
\(\Rightarrow\widehat{EMN}=\widehat{AMB}\)
\(\Rightarrow\Delta_VAMB=\Delta_VHMB\left(ch-gn\right)\)
\(\Rightarrow AM=HM\)
Đồng thời suy ra \(AB=BH\Rightarrow BH=BC\) (do AB=BC)
Theo Pitago: \(\left\{{}\begin{matrix}HN=\sqrt{BN^2-BH^2}\\CN=\sqrt{BN^2-BC^2}\end{matrix}\right.\) \(\Rightarrow CN=HN\)
\(\Rightarrow AM+CN=MH+NH=MN\)
\(\Rightarrow MD+DN+MN=MD+DN+AM+CN=AD+CD=2a\)
Pitago: \(MN^2=DM^2+DN^2\ge\dfrac{1}{2}\left(DM+DN\right)^2\Rightarrow MN\ge\dfrac{\sqrt{2}}{2}\left(DM+DN\right)\)
\(\Rightarrow2a-\left(DM+DN\right)\ge\dfrac{\sqrt{2}}{2}\left(DM+DN\right)\)
\(\Rightarrow2a\ge\left(\dfrac{2+\sqrt{2}}{2}\right)\left(DM+DN\right)\ge\left(2+\sqrt{2}\right).\sqrt{DM.DN}\)
\(\Rightarrow DM.DN\le\left(6-4\sqrt{2}\right)a^2\)
\(\Rightarrow S_{MDN}=\dfrac{1}{2}DM.DN\le\left(3-2\sqrt{2}\right)a^2\)
Dấu "=" xảy ra khi \(DM=DN=\left(\sqrt{6}-\sqrt{2}\right)a\)
Cho hình bình hành ABCD có 2AB=BC=2a, góc B =60 độ . Gọi M,N lần lượt là trung điểm của AD và BC
a) Tứ giác AMNB là hình gì ? Vì sao ?
b) CMR : An vuông góc với ND ; AC=ND
c) Tính diện tích của tứ giác AMNB và tam giác AND theo a
a) tứ giác AMNB
có BN // AM (BC // AD)
BN = AM (BC=AD, N;M là Tđiểm BC;AD)
=> AMNB là HBH
2AB = AD, 2AM = AD => AM =AB
=> AMNB là HThoi ( vì là HBH có 2 cạnh kề = nhau )
b) AMNB là Hthoi
=> AN là tia Phân giác của ^BNM
^BNM = 120* (là góc TCP vs ^B)
=> ^ANM = ^BNM /2 = 120*/2 = 60*
t/ tự ta có MNCD là Hthoi
=> ND là tia Phân giác của ^MNC
^MNC = 60* (là góc TCP vs ^NCD, mà ^NCDlà góc TCP vs ^B)
=> ^MND = ^MNC/2 = 30*
có ^AND = ^ANM + ^MND = 60* + 30* = 90*
=> AN vuông vs N
tam giác BAN cân tại B ( AB = BN t/c Hthoi )
^B =60* (gt)
=> tg BAN đều
=> AN = BA
AB = CD (t/c HBH )
=> AN = CD
^ANC = ^ANM + ^MNC , ^MNC =60*= ^B (2 góc đồng vị)
=> ^ANC = 60* +60* =120*
xét tg ANC và tg NCD
có NC chung
^ANC = ^NCD (=120*)
AN = CD (cmt)
=> tg ANC = tg NCD (cgc)
=> AC = ND ( 2 cạnh t/ứ)
c) gọi O là giao cuả BM và AN
có AMNB là Hthoi (cm câu a)
=> BM vuông vs AN (t/c Hthoi)
BM cắt AN tại trung điểm mỗi đường
=> O là trung điểm AN
có tam giác BAN đều (cm câu b)
=> AN = AB = a
mà O là trung điểm AN (cmt).
=> AO = ON = AN/2 = a/2
xét tg BON vuông tại O
có \(BO^2+ON^2=BN^2=>BO^2=BN^2-ON^2=a^2-\left(\dfrac{a}{2}\right)^2=\dfrac{3a^2}{4}=>BN=\dfrac{\sqrt{3}a}{2}\)
có O là trung điểm BM (T/C Hthoi )
=> BM = 2BO = 2\(\dfrac{\sqrt{3}a}{2}\)=\(\sqrt{3}a\)
S Hthoi ABMN = \(\dfrac{1}{2}AN.BM=\dfrac{1}{2}a.\sqrt{3}a=\dfrac{a^2\sqrt{3}}{2}\)
xét tứ giác AMDN có BN // MD, BN = MD =a
=> AMDN là HBH
=> BM = ND ( t/c HBH )
=> ND = \(\sqrt{3}a\)
S tam giác AND = \(\dfrac{1}{2}AN.ND=\dfrac{1}{2}a.\sqrt{3}a=\dfrac{a^2\sqrt{3}}{2}\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là trung điểm của các cạnh AB và AD; H là giao điểm của CN và DM. Biết SH vuông góc với mặt phẳng ( ABCD ) và S H = a 3 . Tính thể tích khối chóp S.CDNM theo a:
A. V = 3 24 a 3
B. V = 5 3 24 a 3
C. V = 3 12 a 3
D. V = 5 3 12 a 3
Vì S H ⊥ A B C D nên
V S . C D M N = 1 3 S H . S . C D M N = 1 3 S H . S A B C D - S B C M - S A M N = 1 3 a 3 5 8 a 2 = 5 3 24 a 3
Đáp án B
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là trung điểm của các cạnh AB và AD; H là giao điểm của CN và DM. Biết SH vuông góc với mặt phẳng (ABCD) và SH = a 3 . Tính thể tích khối chóp S.CDNM theo a.
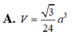
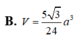
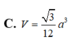
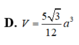
Cho hình vuông ABCD có độ dài cạnh bằng a. Trên cạnh CB,CD lần lượt lấy điểm M,N sao cho chu vi tam giác CMN là 2a. Gọi giao điểm của đường thẳng BD với các đường thẳng AM,AN lần lượt là E,F. Gọi giao điểm của đường thẳng MF và NE là H
a, Tính số đo góc MAN
b, Chứng minh AH vuông góc với MN
c, Gọi diện tích tam giác AMN, AEF lần lượt là S1,S2. Tính \(\frac{S2}{S1}\)
cho hình vuông ABCD có cạnh bằng a. các điểm M,N nằm trên các cạnh BC, CD ( M khác B,M khác C,N khác C,N khác D) sao cho góc MAN=45 độ. gọi E,F lần lượt là giao điểm của AM, AN trên BD
a) chứng minh chu vi tam giác MNC=2a
b) chứng minh rằng MF vuông góc với AN
C) tính diện tích tam giác AMN khi M,N lần lượt là giao điểm của tia phân giác của góc BAC với cạnh BC; tia phân giác của góc DAC với cạnh CD và a=4cm
Cho hình vuông ABCD có cạnh bằng a. Trên BC lấy M, trên tia đối của tia DC lấy N sao cho BM = DN. Vẽ AH vuông góc với NM ( H thuộc NM), AH cắt DC tại E. Gọi G là giao điểm của MN với AD
a, CMR tam giác NAM vuông cân bà D, H, B thẳng hàng
b, Tính chu vi tam giác EMC theo a
c, Gọi I là giao điểm của BD với AM, gọi K là giao điểm của EG với AN. CMR: tứ giác AIEK là hình vuông