a) Tìm giá trị của x2 với x lần lượt bằng 2; 3; 4; 5; 10.
b) Tìm số thực không âm x với x2 lần lượt bằng 4; 9; 16; 25; 100.
Cho hàm số y = -3 x 2 . Lập bảng các giá trị của y ứng với các giá trị của x lần lượt bằng : -2 ; -1 ; -1/3 ; 0 ; 1/3 ; 1 ; 2
Cho hàm số y = 3 x 2 . Lập bảng tính các giá trị của y ứng với các giá trị của x lần lượt bằng : -2 ; -1 ; -1/3 ; 0 ; 1/3 ; 1 ; 2
Ký hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [0;2]. Giá trị của a+A bằng
A. 19 3
B. 22 3
C. 7
D. 12
Chọn C
Hàm số y =
x
2
+
x
+
4
x
+
1
là hàm phân thức có tập xác định là ![]() nên nó liên tục trên [0;2], từ đó ta vận dụng quy tắc tìm giá trị lớn nhất và nhỏ nhất không cần xét dấu đạo hàm.
nên nó liên tục trên [0;2], từ đó ta vận dụng quy tắc tìm giá trị lớn nhất và nhỏ nhất không cần xét dấu đạo hàm.
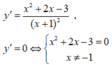
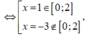
Ta có ![]()
=> A = 4, a = 3.
Vậy a + A = 7.
Ký hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [0;2]. Giá trị a+A bằng
![]()
![]()
![]()
![]()
Ký hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [ 0;2]. Giá trị a+ A bằng
A. 7
B. 18
C. 0
D. 12
Kí hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn 0 ; 2 . Khi đó giá trị của a + A bằng:
A. 7
B. 18
C. 0
D. 12
Gọi a,b lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + log 3 1 - x trên đoạn [-2;0]. Tổng a+b bằng
A. 5
B. 7
C. 6
D. 0
Gọi a;b lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + log 2 2 - x trên đoạn [-2;0]. Tổng a + b bằng
A. 5.
B. 0.
C. 7.
D. 6.
Hàm số \(y=f\left(x\right)\) được cho bởi công thức \(y=3x^2-7\)
a) Tìm giá trị của x tương ứng với các giá trị của y lần lượt bằng: \(-4;5;-6\dfrac{2}{3}\)
Helpppppppppppppppppppp ![]()
\(y=-4\\ \Rightarrow-4=3x^2-7\\ \Rightarrow3x^2=3\\ \Rightarrow x^2=1\\ \Rightarrow x=\pm1\)
\(y=5\\ \Rightarrow5=3x^2-7\\ \Rightarrow3x^2=12\\ \Rightarrow x^2=4\\ \Rightarrow x=\pm2\)
\(y=-6\dfrac{2}{3}\\ \Rightarrow-6\dfrac{2}{3}=3x^2-7\\ \Rightarrow3x^2=\dfrac{1}{3}\\ \Rightarrow x^2=\dfrac{1}{9}\\ \Rightarrow x=\pm\dfrac{1}{3}\)