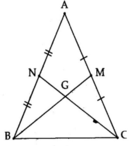
Trong tam giác ABC ở ví dụ 1, cho trung tuyến BN và GN = 1 cm. Tính GB và NB.

Những câu hỏi liên quan
cho tam giác ABC,BN là đường trung tuyến G là trọng tâm của tam giác ABC
1)chứng minh GM=1 phần 3 BN
2)chứng minh GB=2 GN
3)biết GN=2.tính BG,BN
1: Vì G là trọng tâm
nên BG=2/3BN
=>GM=1/3BN
2: BG/GM=2/3:1/3=2
=>BG=2GN
3: BG=2*GN=4cm
BN=4+2=6cm
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A. Biết AB = 8cm, AC = 6cm
a. Tính BC
b. Vẽ ba đường trung tuyến AM, BN, CP. Gọi G là trọng tâm của tam giác ABC. Tính BN và CP
c. Tính GN và GC
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có hai đường trung tuyến BM, CN.
a) Chứng minh nếu tam giác ABC cân tại A thì BM = CN.
b) Ngược lại nếu BM = CN, chứng minh:
i) GB = GC, GN = GM;
ii) BN = CM;
iii) tam giác ABC cân tại A.
Cho tam giác ABC. Hai đường trung tuyến AM và BN cắt nhau tại G.
Tìm các số a, b biết: \(\overrightarrow {AG} = a.\overrightarrow {AM} ;\overrightarrow {GN} = b.\overrightarrow {GB} \)
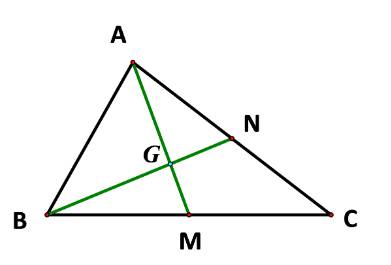
Ta có: \(\overrightarrow {AG} ,\overrightarrow {AM} \)là hai vecto cùng hướng và \(\left| {\overrightarrow {AG} } \right| = \frac{2}{3}\left| {\overrightarrow {AM} } \right|\)
Suy ra \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} .\) Vậy \(a = \frac{2}{3}.\)
Ta có: \(\overrightarrow {GN} ,\overrightarrow {GB} \)là hai vecto ngược hướng và \[\left| {\overrightarrow {GN} } \right| = \frac{1}{3}BN = \frac{1}{2}.\left( {\frac{2}{3}BN} \right) = \frac{1}{2}\left| {\overrightarrow {GB} } \right|\]
Suy ra \(\overrightarrow {GN} = - \frac{1}{2}\overrightarrow {GB} .\) Vậy \(b = - \frac{1}{2}.\)
Đúng 0
Bình luận (0)
cho tam giác abc . các đường trung tuyến AM , AB , CF cắt nhau tại G
A, So sánh GN với GB , GN vs BN , GB vs BN
b, tính tỉ số \(\frac{\text{diện tích tam giác ABG }}{\text{diện tích tam giác ABM }}\)
a, do 3 đường trung tuyến cắt nhau tại G
=> G là trọng tâm
=> GN=1/2 BG
GN=1/3 BN
GB=2/3BN
Đúng 0
Bình luận (0)
câu b em có ghi nhầm đề ko vậy
hok tốt
nếu sai gửi qua ib nha
Đúng 0
Bình luận (0)
Trong tam giác ABC, các trung tuyến AM, BN, CP cắt nhau tại G. Gọi K là trung điểm GB. CM: Các cạnh của tam giác GMK = 1/3 các trung tuyến của tam giác ABC.
Cho tam giác ABC có 2 đường trung tuyến BM, CN cắt nahu tại điểm G.
a, C/m nếu tam giác ABC cân tại A thì BM = CN.
b, Ngược lại nếu BM = CN , c/m:
i,GB = GC, GN = GM;
ii, BN = CM
iii, Tam giác ABC cân tại A
cho tam giác abc có 3 đường trung tuyến am,bn và cp. các đoạn thẳng cp và bn cắt nhau tại g.biết rằng ga=4cm, gb=gc=6cm
a. tính độ dài các đường trung tuyến của tam giác abc.
b. chứng minh tam giác abc cân
Cho tam giác HPG có 3 trung tuyến HM,PA,GB cắt nhau tại T . Biết TH = 3 cm,TP=TG=4 cm a, Tính HM,PA,GB. b, Chứng minh tam giác HPG cân
Đúng 0
Bình luận (0)
cho tam giac ABC đg trung tuyến BM trên BM lấy G, K sao cho GB=2/3GM và G là trung điểm của BK
N là trung điểm của KC GN cắt CM ở O cm
a, O là trọng tâm của tam giac GKC
b, GO= 1/3BC