Cho Hình 3.41.
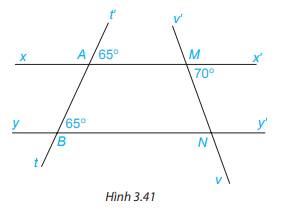
a) Giải thích tại sao xx’//yy’.
b) Tính số đo góc MNB.
Những câu hỏi liên quan
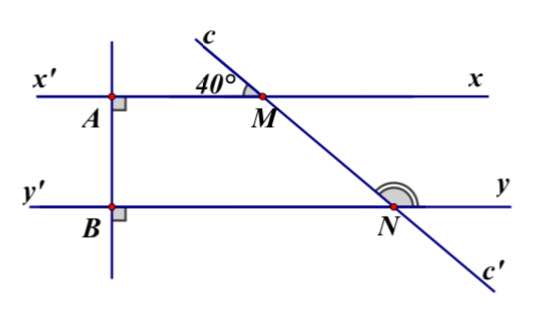
Cho hình vẽ biết AB⊥xx' tại A;AB⊥yy' tại B
cc' cắt xx’ tại M ,cc’ cắt yy’ tại N sao cho AMc =40º
a) Chứng minh rằng :
b) Tính số đo MNy
c) Tia phân giác của NMAvà tia phân giác
của MNB cắt nhau tại O. Tính số đo MON từ đó suy ra MO⊥NO.
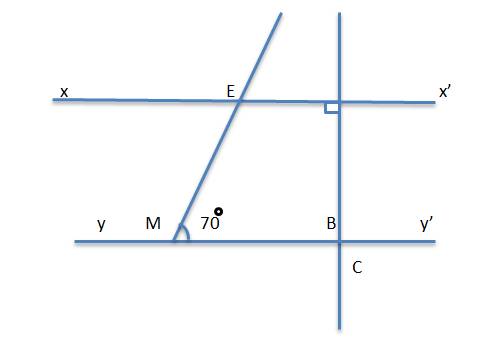
vẽ 2 đường thẳng xx' và yy' cùng vuông góc với đường thẳng C lần lượt tại A và B . Trên yy' lấy điểm M sao cho BM = 4cm vã tia Mz cắt xx' tại E sao cho EMB = 70 độ
a, Giải thích vì sao xx' // yy'
b tính các góc tạo thành của xx' và tia Mz
a) Ta có:
\(xx'\perp C\left(gt\right)\)
\(yy'\perp C\left(gt\right)\)
\(\Rightarrow xx'//yy'\)
b) Ta có: \(xx'//yy'\) và tia \(Mz\) cắt \(xx'\) nên:
\(\widehat{xEM}=\widehat{EMB}\) (so le trong)
\(\Rightarrow\widehat{xEM}=70^o\)
Mà: \(\widehat{xEM}\) đối đỉnh với \(\widehat{zEA}\) nên:
\(\Rightarrow\widehat{zEA}=\widehat{xEM}=70^o\)
\(\widehat{xEz}+\widehat{zEA}=180^o\) (kề bù)
\(\Rightarrow\widehat{xEz}=180^o-70^o=110^o\)
\(\widehat{MEA}+\widehat{xEM}=180^o\) (kề bù)
\(\Rightarrow\widehat{MEA}=180^o-70^o=110^o\)
Đúng 1
Bình luận (0)
Cho hai đường thẳng xx và yy cắt nhau tại O. Biết
x
O
y
^
45
°
.a) Tính số đo các góc
x
O
y
^
,
x
O
y
^
và
x
O
y...
Đọc tiếp
Cho hai đường thẳng xx' và yy' cắt nhau tại O. Biết x O y ^ = 45 ° .
a) Tính số đo các góc x ' O y ' ^ , x O y ' ^ và x ' O y ^ .
b) Trên tia Ox lấy điểm A khác O. Kẻ đường thẳng aa' đi qua A và song song với yy'. Kẻ được bao nhiêu đường thẳng aa' như vậy? Vì sao?
c) Chỉ ra các góc ở đỉnh A có số đo bằng 45 ° và giải thích
Cho 2 đường thẳng xx' và yy' cắt nhau tại điểm O,sao cho góc xOy=90o.
a)Hãy vẽ hình
b)Tính số đo các góc còn lại trên hình vẽ
Nhận thầy từ hình vẽ hai góc xOy và x'Oy' là hai góc đối đỉnh
Mà xOy = 90 độ => xOy = x'Oy' = 90 độ
Có hai góc xOy + xOy' = 180 độ (kề bù do đối đỉnh)
=> 90 độ + xOy' = 180 độ
=> xOy' = 90 độ
Thấy xOy' và x'Oy đối đỉnh mà xOy' = 90 độ
=> xOy' = x'Oy = 90 độ
Đúng 0
Bình luận (0)
a)
b)
góc xOy=x'Oy'=90*(đối đỉnh)Vì góc xOy kề bù với yOx'nên: xOy+yOx'=180*
hay:90*+yOx'=180*
=> yOx'=180*-90*
Vậy yOx'=90*
yOx'=xOy'=90*(đối đỉnh)
^...^ 
^_^
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho 2 đường thẳng xx' và yy' cắt nhau tại O sao cho góc xOy bằng 70 độ a) kể tên các cặp góc kề bù và đối đỉnh có trong hình b) tính số đo góc xOy'
a) Các cặp góc kề bù
\(\widehat{xOy}\) và \(\widehat{yOx'}\)
\(\widehat{yOx'}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy'}\) và \(\widehat{xOy'}\)
\(\widehat{xOy'}\) và \(\widehat{xOy}\)
Các cặp góc đối:
\(\widehat{xOy}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy}\) và \(\widehat{y'Ox}\)
b) Do \(\widehat{xOy}\) kề bù với \(\widehat{xOy'}\)
\(\Rightarrow\widehat{xOy}+\widehat{xOy'}=180^o\)
\(\Rightarrow\widehat{xOy'}=180^o-70^o=110^o\)
Đúng 1
Bình luận (0)
Cho hai đường thẳng xx' và yy' giao nhau tại O sao cho góc xOy= 45 độ. Tính số đo các góc còn lại trong hình vẽ
ta có: xx' cắt yy' tại O
=> góc xOy = góc x'Oy' =45 độ ( đối đỉnh)
=> góc x'Oy' = 45 độ
mà góc xOy + góc x'Oy = 180 độ ( kề bù)
Thay số: 45 độ + góc x'Oy = 180 độ
góc x'Oy = 180 độ - 45 độ
góc x'Oy = 135 độ
mà góc x'Oy = góc xOy' = 135 độ ( đối đỉnh)
=> góc xOy' = 135 độ
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho hai đường thẳng xx’ và yy’ cắt đường thẳng aa’ tại A và B, số đo góc
x
A
B
⏜
80
o
. Xác định số đo góc
y
B
a
⏜
để có xx’ // yy’ A. 60° B. 80° C. 120° D. 150°
Đọc tiếp
Cho hai đường thẳng xx’ và yy’ cắt đường thẳng aa’ tại A và B, số đo góc x A B ⏜ = 80 o . Xác định số đo góc y B a ' ⏜ để có xx’ // yy’
A. 60°
B. 80°
C. 120°
D. 150°
Cho 2 đường thẳng xx' và yy' cắt nhau tại O tạo thành góc xOy có số đo = 40 độ
a) Tính số đo góc x'Oy' và góc xOy'
b) lấy điểm A thuộc tia Ox'( A khác O), vẽ tia At sao cho góc tAx'= 140 độ( tia At cùng phía với tia Oy đối với nửa mặt phẳng có bờ xx'). Chứng minh At // yy'
ban co the giup minh tra loi cau hoi nay duoc khong
Đúng 0
Bình luận (0)
a)Ta có:\(\widehat{xOy}\)+\(\widehat{xOy'}\)=180độ
40 độ +\(\widehat{xOy'}\)=180độ
\(\widehat{xOy'}\)=140 độ
Vì \(\widehat{xOy}=\widehat{x'Oy'}\)=>\(\widehat{x'Oy'}\)=40 độ
Vậy \(\widehat{x'Oy'}\)=40 độ;\(\widehat{xOy'}\)=140 độ
b)Ta có:\(\widehat{x'Ot}+\widehat{tAx}\)=180độ
140 độ+\(\widehat{tAx}\)=180 độ
\(\widehat{tAx}\)=40 độ
mà \(\widehat{xOy}\)=40 độ
=>\(\widehat{xOy}=\widehat{xAt}\)
mà hai góc này ở vị trí so le trong =>At//yy'
Đúng 0
Bình luận (0)
cho 2 đường thẳng song song xx'va yy'.Trên xx' va yy' lần lượt lấy hai điểm AB sao cho AB phân biệt yy' tại B
a. Chứng minh AB phân biệt xx'
b. Trên By' lấy điểm C Trên Ax' lấy điểm D sao cho BCD = 120 độ Tính số đo các góc ADC CDx' DCy'
(Nếu được xin các cao nhân vẽ hình dùm 😅