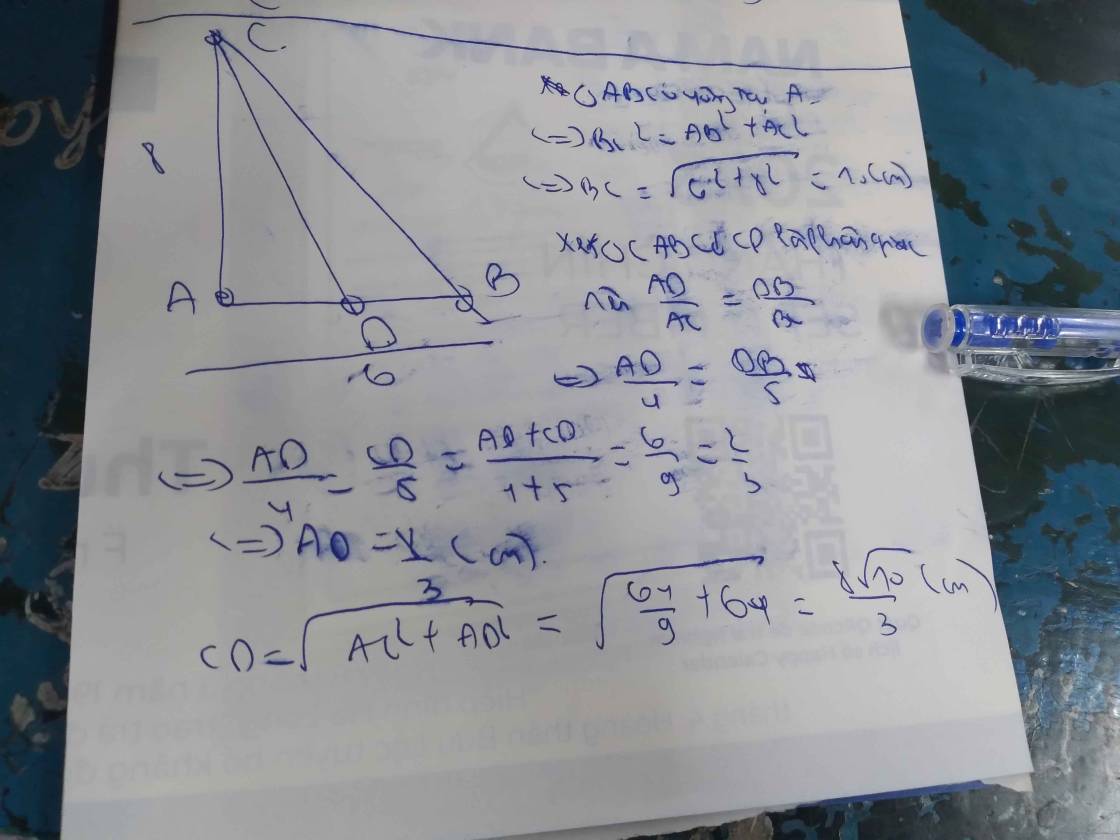
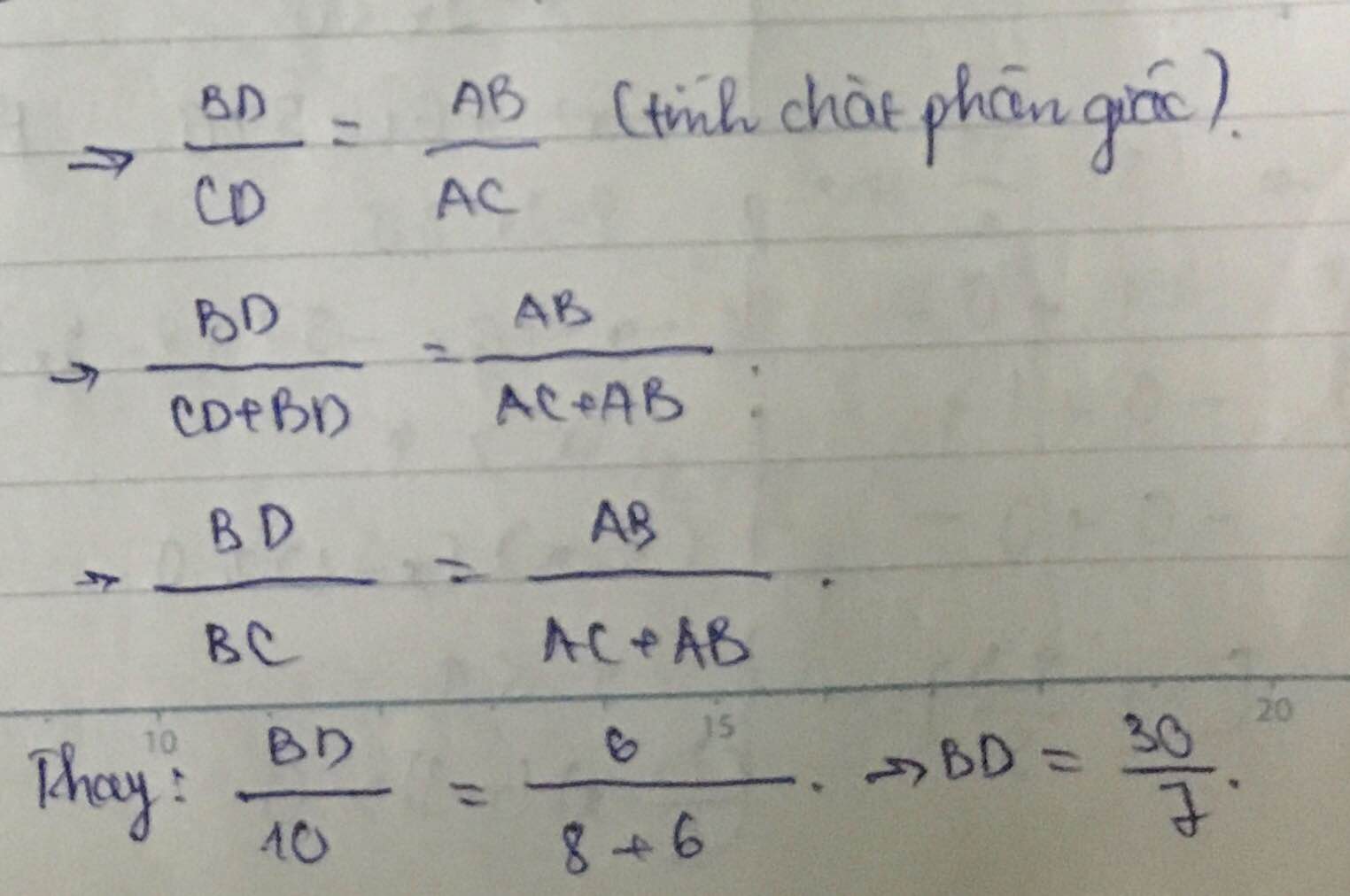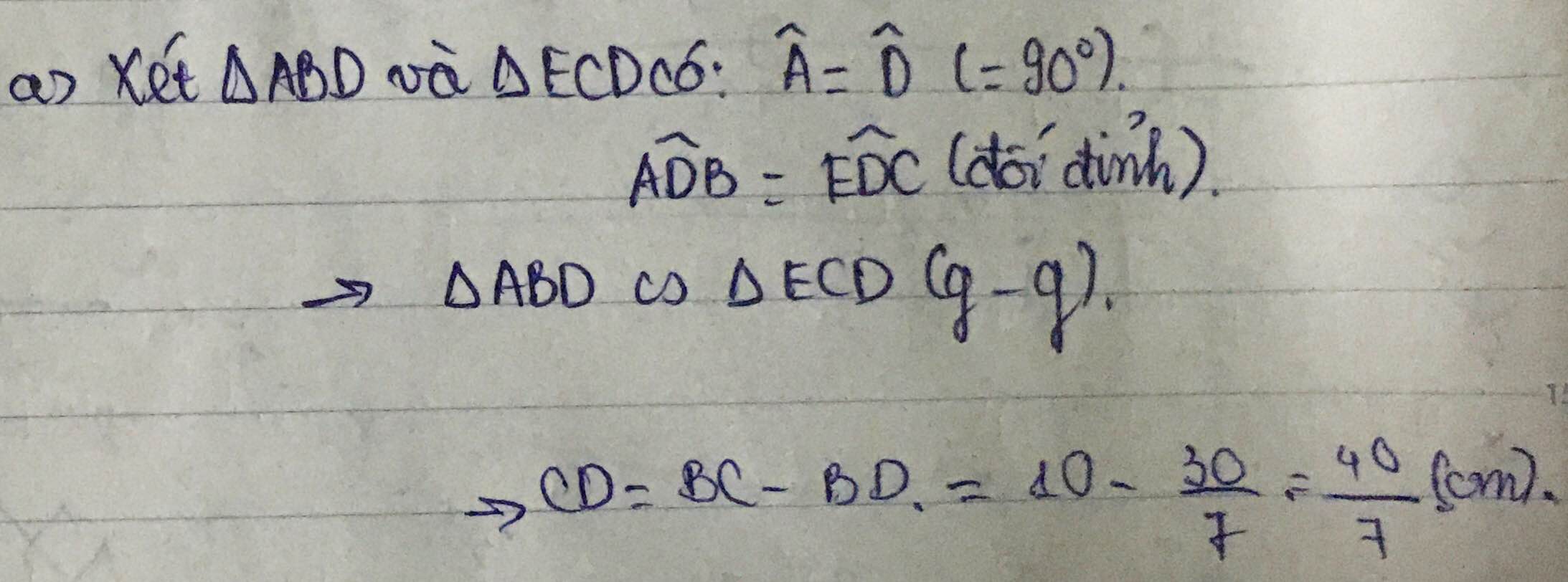Cho tam giác ABC vuông tại A, có AB=6cm và AC= 8cm. Tính độ dài đường phân giác trong CD

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB=6cm; AC= 8cm. Tính độ dài đường phân giác trong CD
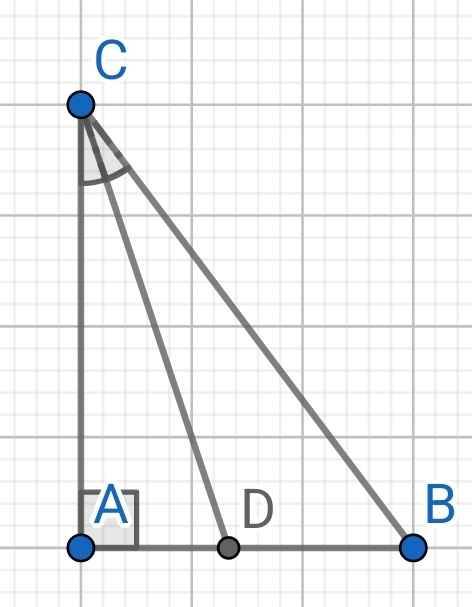 Do ∆ABC vuông tại A
Do ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do CD là phân giác (gt)
⇒ AD/AC = BD/BC
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
AD/AC = BD/BC = (AD + BD)/(AC + BC) = AB/(AC + BC) = 6/18 = 1/3
AD/AC = 1/3 ⇒ AD = AC.1/3 = 8/3 (cm)
∆ACD vuông tại A
⇒ CD² = AC² + AD² (Pytago)
= 8² + (8/3)²
= 640/9
⇒ CD = 8√10/3 (cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, AB=6cm, AC =8cm. Phân giác AD.
a)Tính độ dài BD và CD b) Kẻ DH vuông góc với AB. Tính DH, AD .
Cho tam giác ABC vuông tại A có AB=6cm,AC=8cm,đường cao AH,tia phân giác của góc A cắt BC tại D
a)Tính độ dài đoạn thẳng BC và CD?
b)Tính chiều cao AH của tam giác ABC
c)Lấy điểm E sao cho tứ giác ADCE là hình bình hành.Kẻ EM vuông góc với AC(M thuộc AC), AN vuông góc với CE(N thuộc tia CE) Chứng minh tam giác HAC đồng dạng với tam giác MEA và CD.CH+CE.CN=AC^2
a: BC=căn 6^2+8^2=10cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=10/7
=>BD=30/7cm; CD=40/7cm
b: AH=6*8/10=4,8cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AB=6cm, AC=8cm. Đường phân giác của góc BAC cắt cạnh BC tại D.
a.tính độ dài BC và độ dài CD
b. Kẻ đường thẳng qua D vuông góc với BC và cắt AC tại E. Chứng minh tam giác DEC đồng dạng tam giác ABC
c. Chứng minh tam giác DBE cân.
Cho tam giác ABC vuông tại A có AB = 6cm ; AC= 8cm . Đường cao AH và phân giác BD cắt nhau tại I ( H trên BC và D trên AC ) .
a) Tính độ dài AD , DC
b) Cm : tam giác ABC đồng dạng với tam giác HBA và AB^2 = BH.BC
c) Cm : tam giác ABI đồng dạng với tam giác CBD
d) Cm : \(\dfrac{IH}{IA}=\dfrac{AD}{DC}\)
( Giải giúp mình câu c với d ạ cảm ơn ^^ )
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100\)
hay BC=10cm
Xét ΔABC có BD là đường phân giác ứng với cạnh AC
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)
mà AD+CD=8
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó: AD=3cm; CD=5cm
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Suy ra: \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
hay \(AB^2=BH\cdot BC\)
Đúng 3
Bình luận (1)
c) Ta có: \(\widehat{ABD}=\widehat{DBC}\)( BD là phân giác )\(\Rightarrow90^0-\widehat{ABD}=90^0-\widehat{DBC}\Rightarrow\widehat{BIH}=\widehat{ADI}\Rightarrow\widehat{AID}=\widehat{ADI}\Rightarrow\Delta ADI\) cân tại A\(\Rightarrow AI=AD\Rightarrow\dfrac{AB}{AI}=\dfrac{AB}{AD}\)
Xét Δ ABI và Δ CBD có:
\(\widehat{BAI}=\widehat{BCD}\left(\Delta ABC\sim\Delta HBA\right)\)
\(\dfrac{AB}{AI}=\dfrac{BC}{CD}\left(=\dfrac{AB}{AD}\right)\)
\(\Rightarrow\Delta ABI\sim\Delta CBD\left(c.g.c\right)\)
d) Xét ΔABH có:
BI là tia phân giác của \(\widehat{ABH}\)
\(\Rightarrow\dfrac{IH}{IA}=\dfrac{BH}{AB}\left(1\right)\)( tính chất tia phân giác)
Xét ΔABC có:
BD là tia phân giác của \(\widehat{ABC}\)
\(\Rightarrow\dfrac{AD}{DC}=\dfrac{AB}{BC}\left(2\right)\)( tính chất tia phân giác)
Ta có: \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\left(\Delta ABC\sim\Delta HBA\right)\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\left(đpcm\right)\)
Đúng 1
Bình luận (0)
c: Xét ΔABI và ΔCBD có
\(\widehat{ABI}=\widehat{CBD}\)
\(\widehat{BAI}=\widehat{BCD}\left(=90^0-\widehat{ABH}\right)\)
Do đó: ΔABI\(\sim\)ΔCBD
d: Xét ΔBHA có BI là đường phân giác ứng với cạnh AH
nên \(\dfrac{IH}{IA}=\dfrac{BH}{BA}\left(1\right)\)
Xét ΔBAC có BD là đường phân giác ứng với cạnh AC
nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}\left(2\right)\)
Ta có: \(AB^2=BH\cdot BC\)
nên \(\dfrac{BH}{BA}=\dfrac{AB}{BC}\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra \(\dfrac{IH}{IA}=\dfrac{AD}{DC}\)
Đúng 1
Bình luận (0)
4. Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm. Kẻ đường cao AH và phân giác AD của tam giác ABC (H; D thuộc BC).
1) Tính độ dài các đoạn thẳng DB; DC
2) Tính độ dài các đoạn thẳng HD; AD
1: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{6}=\dfrac{CD}{8}\)
mà BD+CD=10cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{6}=\dfrac{CD}{8}=\dfrac{BD+CD}{6+8}=\dfrac{10}{14}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{30}{7}cm;CD=\dfrac{40}{7}cm\)
Đúng 3
Bình luận (0)
Bài 5 (3,5 điểm) Cho tam giác ABC vuông tại A có AB 6cm; AC 8cm, đường cao AH và phân giác BD cătnhau tại I (H thuộc BC, D thuộc AC)a) Tính độ dài AD, DC
Đọc tiếp
Bài 5 (3,5 điểm) Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm, đường cao AH và phân giác BD căt
nhau tại I (H thuộc BC, D thuộc AC)
a) Tính độ dài AD, DC
\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
BD là phân giác
=>DA/AB=DC/BC
=>DA/3=DC/5=8/8=1
=>DA=3cm; DC=5cm
Đúng 1
Bình luận (0)
Bài 6:cho tam giác ABC vuông tại A, AB=6cm, AC=8cm. Phân giác AD
a)Tính độ dài BD và CD
b)Kẻ DH vuông góc với AB. Tính DH, AD
a, dùng pytago tính ra BC = 10 cm
tam giác ABC có AD là phân giác (gt)
=> CD/AC = BD/AB (tính chất)
=> CD + DB/AB+AC = CD/AC + BD/AB
AB = 6; AC = 8; BC = 10 và CD + DB = BC
=> 10/14 = CD/8 = BD/6
=> CD = 40/7 và BD = 30/7
Cho tam giác ABC vuông ở A , AB=6cm; AC=8cm; BC=10cm có đường cao AH cắt cạnh BC tại H, đường phân giác BD của góc ABC cắt AC tại D.
a) Tính độ dài các đoạn thẳng AD và DC .
b) Tính AH=?
a/ \(BD\) là đường phân giác \(\widehat{BAC}\)
\(\to\dfrac{DA}{DC}=\dfrac{BA}{BC}\) hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\to\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{AC}{8}=\dfrac{8}{8}=1\)
\(\to\begin{cases}DA=3\\DC=5\end{cases}\)
b/ \(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.AH.BC\)
\(\to AB.AC=AH.BC\)
\(\to \dfrac{AB.AC}{BC}=AH=\dfrac{6.8}{10}=3,2(cm)\)
Đúng 1
Bình luận (0)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm
Đúng 0
Bình luận (0)