Gọi A, B, C, D, E là các điểm trên đồ thị hàm số y=2x−1 có hoành độ x lần lượt là -2; -1; 0; 1; 2. Từ kết quả của HĐ4, hãy xác định tọa độ các điểm A, B, C, D, E

Những câu hỏi liên quan
Cho hàm số y=f(x)=x+3/2.|x|
a, Vẽ đồ thị hàm số trên
b, Gọi E và F là 2 điểm thuộc đồ thị hàm số trên có hoành đọ lần lượt là -4 và 4/5. Xác định tọa độ của 2 điểm E và F để 2 điểm ME + MF là nhỏ nhất
Cho hàm số y = f(x) = 2/3x có đồ thị là (d)
a)Vě (d)
c)Tìm giá trị nhỏ nhất của y khi -6 d)Gọi A,B là hai điểm thuộc (d) có hoành độ lần lượt là -2,5 và 4. Tìm trên đoạn thắng AB
những điểm có tọa độ là các số nguyên.
Cho hàm số y = f(x) = mx + 2m − 3 có đồ thị (d). gọi A, B là hai điểm thuộc đồ thị
và có hoành độ lần lượt là −1 và 2.
1 Xác định tọa độ hai điểm A và B.
2 Tìm m để cả hai điểm A và B cùng nằm phía trên trục hoành.
3 Tìm điều kiện của m để f(x) > 0, ∀x ∈ [−1; 2]
a, Vẽ đồ thị hàm số y=x√2y
b, Xác định tung độ các điểm A, B, C thuộc đồ thị có hoành độ lần lượt là -1; 1; 2 c, Tính khoảng cách từ A, B, C đến gốc tọa độ. d, Gọi αlà góc tạo bởi đồ thị với trục Ox. Tính số đo góc α.
1/ Cho mặt phẳng tọa độ Oxy.
a) Vẽ đồ thị hàm số y=2x
b)Tìm tung độ các điểm A, B, C nằm trên đồ thị đó có hoành độ lần lượt là -1, 2 và 3
biết đồ thị hàm số y = ax đi qua A(-3,2).
a,tìm hệ số a và vẽ đo thị hàm số.
b,biết đô thị hàm số trên đi qua 2 điểm D và E với hoành độ của D là 1.5 và tung độ của E là -4.hãy tìm tọa độ cửa các điểm D và E.
c,tìm trên đồ thị điểm có tung độ gấp 2 lần hoành độ
a, có gt x = -3
gt y = 2
=> a = 2 : (-3) = \(\frac{-2}{3}\)
b, D (1,5;-1)
E (-4;6)
c, A (4;2)
Đúng 0
Bình luận (0)
a) Vẽ đồ thị hàm số y=1,5x và y=-2x, trên cùng một mặt phẳng tọa độ
b)Điểm A(2/9;1/3) ; B(2/7;-3/7) có thuộc đồ thị hàm số y= 3/2x hay không ?
c) Điểm E thuộc đồ thị hàm số trên và có hoành độ là 8/15 . Tìm trung độ
d)Điểm N thuộc đồ thị hàm số y=3/2x và có trung độ là 5/3 . TÌm tọa độ điểm N
Gọi (C) là đồ thị hàm số
y
x
-
7
x
+
1
, A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho
0
x
M
3
, tìm giá trị lớn nhất của diện tích
∆
A
B
M
A. 3 B. 5 C. 6 D....
Đọc tiếp
Gọi (C) là đồ thị hàm số y = x - 7 x + 1 , A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho 0 < x M < 3 , tìm giá trị lớn nhất của diện tích ∆ A B M
A. 3
B. 5
C. 6
D. 3 5
Đáp án A
Phương pháp:
- Gọi tọa độ điểm M thuộc đồ thị hàm số.
- Tính khoảng cách từ M đến AB suy ra diện tích.
- Từ đó sử dụng phương pháp hàm số tìm GTLN của diện tích tam giác ABM.
Cách giải:

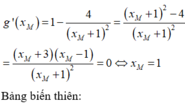

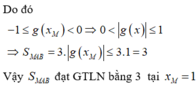
Đúng 0
Bình luận (0)
Gọi (C) là đồ thị hàm số
y
x
-
7
x
+
1
, A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho 0xM3, tìm giá trị lớn nhất của diện tích
∆
A
M
B
A. 3 B. 5 C. 5 D. 3
5
Đọc tiếp
Gọi (C) là đồ thị hàm số y = x - 7 x + 1 , A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho 0<xM<3, tìm giá trị lớn nhất của diện tích ∆ A M B
A. 3
B. 5
C. 5
D. 3 5
Cho hai hàm số y dfrac{1}{2}x^2 và y x2.a.Vẽ đồ thị của hai hàm số này trên cùng mặt phẳng tọa độ .b.Tìm tọa độ hai điểm A ; B có cùng hoành độ x 2 theo thứ tự nằm trên hai đồ thị .c.Gọi A’ và B’ lần lượt là các điểm đối xứng với A ; B qua trục tung Oy . Kiểm tra xem A’ ; B’ có lần lượt nằm trên hai đồ thị đó không ?
Đọc tiếp
Cho hai hàm số y = \(\dfrac{1}{2}x^2\) và y = x2.
a.Vẽ đồ thị của hai hàm số này trên cùng mặt phẳng tọa độ .
b.Tìm tọa độ hai điểm A ; B có cùng hoành độ x = 2 theo thứ tự nằm trên hai đồ thị .
c.Gọi A’ và B’ lần lượt là các điểm đối xứng với A ; B qua trục tung Oy . Kiểm tra xem A’ ; B’ có lần lượt nằm trên hai đồ thị đó không ?
a: 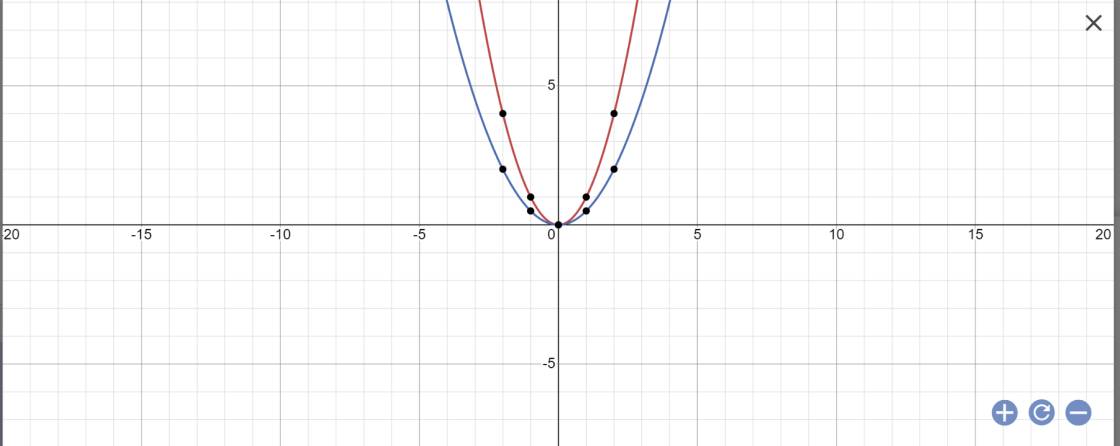
b: Khi x=2 thì y=1/2*2^2=2
=>A(2;2)
Khi x=2 thì y=2^2=4
=>B(2;4)
c: Tọa độ A' là:
\(\left\{{}\begin{matrix}x_{A'}=-x_A=-2\\y_{A'}=y_A=2\end{matrix}\right.\)
Vì f(-2)=1/2*(-2)^2=2
nên A' thuộc (P1)
Tọa độ B' là:
\(\left\{{}\begin{matrix}x_{B'}=-x_B=-2\\y_{B'}=y_B=4\end{matrix}\right.\)
Vì f1(-2)=(-2)^2=4
nên B' thuộc y=x^2
Đúng 2
Bình luận (0)