Các câu hỏi tương tự
Gọi (C) là đồ thị hàm số
y
x
-
7
x
+
1
, A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho
0
x
M
3
, tìm giá trị lớn nhất của diện tích
∆
A
B
M
A. 3 B. 5 C. 6 D....
Đọc tiếp
Gọi (C) là đồ thị hàm số y = x - 7 x + 1 , A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho 0 < x M < 3 , tìm giá trị lớn nhất của diện tích ∆ A B M
A. 3
B. 5
C. 6
D. 3 5
Cho các số thực a, b, c, d thỏa mãn 0 a b c d và hàm số y f(x). Biết hàm số y f(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y f(x) trên
[
0
;
d
]
. Khẳng định nào sau đây là khẳng định đúng? A. M + m f(b) + f(a) B. M + m f(d) + f(c) C. M + m f(0) + f(c) D. M + m f(0) + f(a)
Đọc tiếp
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho hàm số
y
f
x
v
à
y
g
x
là hai hàm liên tục trên R có đồ thị hàm số
y
f
x
là đường cong nét đậm và
y
g
x
là đường cong nét mảnh như hình vẽ. Gọi 3 giao điểm A, B, C của đồ thị
y
f
x...
Đọc tiếp
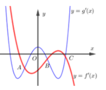
Cho hàm số y = f x v à y = g x là hai hàm liên tục trên R có đồ thị hàm số y = f ' x là đường cong nét đậm và y = g ' x là đường cong nét mảnh như hình vẽ. Gọi 3 giao điểm A, B, C của đồ thị y = f ' x v à y = g ' x trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h x = f x − g x trên đoạn a ; c ?
A. M i n a ; c h x = h 0
B. M i n a ; c h x = h a
C. M i n a ; c h x = h b
D. M i n a ; c h x = h c
Cho hai hàm số yf(x) và yg(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số yf’(x) là đường cong nét đậm, đồ thị hàm số yg’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của yf’(x) và yg’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)f(x)-g(x) trên đoạn [a;c] A.
m
i
n
h
x...
Đọc tiếp
Cho hai hàm số y=f(x) và y=g(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số y=f’(x) là đường cong nét đậm, đồ thị hàm số y=g’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của y=f’(x) và y=g’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [a;c]

A. m i n h x a ; c = h 0
B. m i n h x a ; c = h a
C. m i n h x a ; c = h b
D. m i n h x a ; c = h c
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
.
Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN. A. I(-1;1) B.
I
0
;
-...
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 . Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B. I 0 ; - 3 2
C. I 0 ; 3 2
D. I(-2;2)
Cho đồ thị hàm số
y
e
−
x
2
như hình vẽ, ABCD là hình chữ nhật thay đổi sao cho B,C luôn thuộc đồ thị hàm số đã cho và A,D nằm trên trục hoành. Giá trị lớn nhất của diện tích hình chữ nhật ABCD A.
2
e
B. 2/e C.
2
e
D. ...
Đọc tiếp
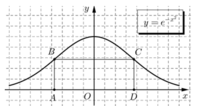
Cho đồ thị hàm số y = e − x 2 như hình vẽ, ABCD là hình chữ nhật thay đổi sao cho B,C luôn thuộc đồ thị hàm số đã cho và A,D nằm trên trục hoành. Giá trị lớn nhất của diện tích hình chữ nhật ABCD
A. 2 e
B. 2/e
C. 2 e
D. 2 e
Cho hàm số
y
x
+
1
x
-
1
có đồ thị (C). Gọi A,B là hai điểm thuộc hai nhánh của (C) và các tiếp tuyến của (C) tại A,B cắt các đường tiệm cận ngang và đứng của (C) lần lượt tại các điểm M,N,P,Q (tham khảo hình vẽ bên). Diện tích tứ giác MNPQ có giá trị nhỏ nhất bằng A. 16. B. 32. C. 8. D. 4.
Đọc tiếp
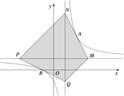
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Gọi A,B là hai điểm thuộc hai nhánh của (C) và các tiếp tuyến của (C) tại A,B cắt các đường tiệm cận ngang và đứng của (C) lần lượt tại các điểm M,N,P,Q (tham khảo hình vẽ bên). Diện tích tứ giác MNPQ có giá trị nhỏ nhất bằng
A. 16.
B. 32.
C. 8.
D. 4.
Cho hàm số
y
−
x
+
1
2
x
−
1
có đồ thị là (C), đường thẳng
d
:
y
x
+
m
. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A, B. Gọi
k
1
,
k
2...
Đọc tiếp
Cho hàm số y = − x + 1 2 x − 1 có đồ thị là (C), đường thẳng d : y = x + m . Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A, B. Gọi k 1 , k 2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A, B. Tìm m để tổng k 1 + k 2 đạt giá trị lớn nhất.
A. m = -1
B. m = -2
C. m = 3
D. m = -5
Cho đồ thị hàm số
C
:
y
1
x
;
điểm M có hoành độ
x
M
2
−
3
thuộc (C). Biết tiếp tuyến của (C) tại M lần lượt cắt Ox, Oy tại A, B. Tính diện tích tam giác OAB. A.
S
Δ
O
A
B
1.
B....
Đọc tiếp
Cho đồ thị hàm số C : y = 1 x ; điểm M có hoành độ x M = 2 − 3 thuộc (C). Biết tiếp tuyến của (C) tại M lần lượt cắt Ox, Oy tại A, B. Tính diện tích tam giác OAB.
A. S Δ O A B = 1.
B. S Δ O A B = 4.
C. S Δ O A B = 2.
D. S Δ O A B = 2 + 3 .