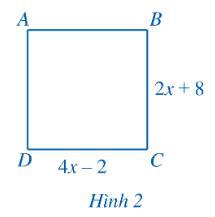
Tìm \(x\), biết tứ giác \(ABCD\) là hình vuông (Hình 2).
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.
a. Tứ giác MNPQ là hình gì? Vì sao?
b. Tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình vuông.
c. Với điều kiện câu b, hãy tính tỉ số diện tích của 2 tứ giác ABCD và MNPQ khi biết AC = a.
Cho tứ giác ABCD có AC = BD và AC vuông góc BD. khi đó : A. Tứ giác ABCD là hình vuông B. Tứ giác ABCD là hình bình hành C. Tứ giác ABCD là hình thoi D. ABCD là tứ giác bất kì
Cho hình tứ giác ABCD đáy lớn là 8.5cm đáy bé là 2.3cm và cạnh bên phải là 7cm. Tìm x biết chu vi hình tứ giác ABCD là 22cm.
\(x+8,5+2,3+7=22\)
\(\Rightarrow x=22-\left(8,5+2,3+7\right)\)
\(\Rightarrow x=22-17,8\)
\(\Rightarrow x=4,2\left(cm\right)\)
Cho tứ giác ABCD. gọi M,N,P,Q lần lượt là trung điểm của AB,AC,DC,DB. Chứng minh tứ giác MNPQ là hình bình hành. Tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình thoi, hình chữ nhật, hình vuông
Câu 8. _NB_ Để chứng minh tứ giác ABCD là hình vuông, dấu hiệu nào sau đây là sai ? A. Tứ giác ABCD là hình thoi có hai đường chéo bằng nhau. B. Tứ giác ABCD là hình thoi có một góc vuông. C. Tứ giác ABCD là hình thoi có hai đường chéo vuông góc. D. Tứ giác ABCD là hình chữ nhật có hai cạnh kề bằng nhau
Trong Hình 12, cho biết \(ABCD\) là một hình vuông. Chứng minh rằng:
a) Tứ giác \(EFGH\) có ba góc vuông
b) \(HE = HG\)
c) Tứ giác \(EFGH\) là một hình vuông
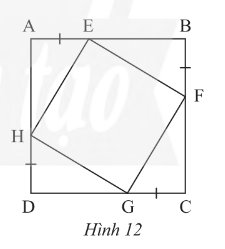
a) Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\); \(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \)
Mà \(AE = BF = CG = HD\) (gt) suy ra \(BE = CF = DG = AH\)
Xét \(\Delta AEH\) và \(\Delta DHG\) ta có:
\(\widehat {\rm{A}} = \widehat {\rm{D}} = 90\)
\(AE = GH\) (gt)
\(AH = DG\) (gt)
Suy ra \(\Delta AEH = \Delta DHG\) (c-g-c)
Suy ra \(\widehat {{\rm{AEH}}} = \widehat {{\rm{DHG}}}\) (hai góc tương ứng)
Mà \(\widehat {AEH} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {DHG} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {EHG} = 90^\circ \)
Chứng minh tương tự ta được \(\widehat {HGF} = 90^\circ ;\;\widehat {GFE} = 90^\circ \)
Vậy tứ giác \(EFGH\) là một góc vuông
b) Vì \(\Delta AEH = \Delta DHG\) (cmt)
Suy ra \(HE = HG\) (2)
Từ (1) và (2) suy ra \(EFGH\) là hình vuông
c) chứng minh tương tự câu b ta có: \(HE = EF\); \(HE = FG\)
Khi đó \(EFGH\) có \(HE = HG = EF = FG\) nên là hình thoi (3)
Tứ giác \(EFGH\) có ba góc vuông nên là hình chữ nhật (4)
Từ (3) và (4) suy ra \(EFGH\) là hình vuông
cho tứ giác ABCD gọi E<F<G<H là trung điểm các cạnh AB<BC<CD<DA luần lượt:
a, Chứng minh tứ gaics AFGH là hình bình hành.
b, tìm điều kiện của tứ giác ABCD để EFGH là hình thoi.
c, tìm điều kiện của tứ giác ABCD để EFGH là hình chữ nhật.
d, tìm điều kiện của tứ giác ABCD để EFGH là hình vuông
E, F lần lượt là trung điểm của AB và BC (gt)
\(\Rightarrow\) EF là đường trung bình của tam giác ABC
\(\Rightarrow\) EF // AC và EF = \(\frac{1}{2}\) AC (1)
H, G lần lượt là trung điểm của AD và DC (gt)
\(\Rightarrow\) HG là đường trung bình của tam giác ACD
\(\Rightarrow\) HG // AC và HG = \(\frac{1}{2}\) AC (2)
Từ (1) và (2) \(\Rightarrow\) EF // HG và EF = HG
\(\Rightarrow\) Tứ giác EFGH là hình bình hành
Tứ giác EFGH là hình bình hành. EF // AC, EF = \(\frac{1}{2}\) AC
Ta còn có EH là đường trung bình của tam giác ABD
\(\Rightarrow\) EH // BD và EH = \(\frac{1}{2}\) BD
- Tứ giác EFGH là hình chữ nhật
\(\Leftrightarrow\) Hình bình hành EFGH có:
\(\widehat{HEF}=90^o\)
\(\Leftrightarrow HE\perp EF\)
\(\Leftrightarrow EH\perp AC\)
\(\Leftrightarrow AC\perp BD\)
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD vuông góc với nhau thì tứ giác EFGH là hình chữ nhật
- Tứ giác EFGH là hình thoi
\(\Leftrightarrow\) Hình bình hành EFGH có: EF = EH \(\Leftrightarrow\) AC = BD
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD bằng nhau thì tứ giác EFGH là hình thoi
- Tứ giác EFGH là hình vuông
\(\Leftrightarrow\) Hình chữ nhật EFGH có: EF = EH \(\Leftrightarrow\) AC = BD
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD vuông góc và bằng nhau thì tứ giác EFGH là hình vuông
Cho tứ giác ABCD gọi M,N,P,Q lần lượt là trung điểm của AB,BC,CD,DA.
a) Tứ giác MNPQ là hình gì ? tại sao?
b) Tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình thoi? hình chữ nhật? hình vuông?
lười gõ =_=
link ây : https://olm.vn/hoi-dap/question/423397.html
tự làm nha
a) Tam giác ABC có :
MA = MB (gt)
NB = NC (gt)
nên MN là đường trung bình của tam giác, do đó MN // AC và MN = AC
Chứng minh tương tự : PQ // AC và PQ = AC
Suy ra MN // PQ và MN = PQ.
Tứ giác MNPQ có hai cạnh đối vừa song song vừa bằng nhau => MNPQ là hình bình hành
b) Theo a), ta có: MQ = 1/2 AD (1)
Xét tam giác ABC có: MA = MB ; NA = NC
=>MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC (2)
Từ (1) và (2) và AD=BC (ABCD là thang cân)
=> MQ = MN
Hình bình hành MNPQ có MQ = MN
=> MNPQ là hình thoi
Trong hình dưới đây diện tích của hình tứ giác ABED lớn hơn diện tích của hình ram giác BEC là 13,6cm vuông . Tính diện tích của hình tứ giác ABCD biết tỉ sồ diện tích tam giác BEC và diện tích hình tứ giác ABED là 2 phần 3
Cho tứ giác ABCD. Lập mệnh đề \(P \Rightarrow Q\) và xét tính đúng sai của mệnh đề đó với:
a) P: “Tứ giác ABCD là hình chữ nhật”, Q: “Tứ giác ABCD là hình bình hành”
b) P: “Tứ giác ABCD là hình thoi”, Q: “Tứ giác ABCD là hình vuông”
a) Mệnh đề \(P \Rightarrow Q\) là: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD là hình bình hành”
Đúng vì mỗi hình chữ nhật đều là hình bình hành.
b) Mệnh đề \(P \Rightarrow Q\) là: “Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD là hình vuông”
Sai vì hầu hết các hình thoi không là hình vuông