Tìm tập xác định của các hàm số:
a) \({\log _2}\left( {3 - 2{\rm{x}}} \right)\);
b) \({\log _3}\left( {{x^2} + 4{\rm{x}}} \right)\).
Tìm tập xác định của các hàm số:
a) \(y = 12{}^x\)
b) \(y = {\log _5}(2x - 3)\)
c) \(y = {\log _{\frac{1}{5}}}\left( { - {x^2} + 4} \right)\)
\(a,D=R\\ b,2x-3>0\\ \Rightarrow x>\dfrac{3}{2}\\ \Rightarrow D=(\dfrac{3}{2};+\infty)\\ c,-x^2+4>0\\ \Rightarrow x^2< 4\\ \Leftrightarrow-2< x< 2\\ \Rightarrow D=\left(-2;2\right)\)
a) Xét hàm số \(y = {\log _2}x\) với tập xác định \(D = \left( {0; + \infty } \right)\).
i) Hoàn thành bảng giá trị sau:
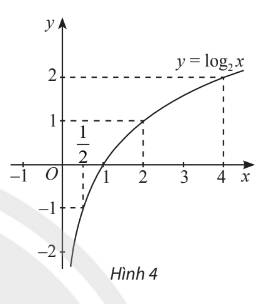
ii) Trong mặt phẳng toạ độ \(Oxy\), xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm \(M\left( {x;{{\log }_2}x} \right)\) với \(x > 0\) và nối lại ta được đồ thị hàm số \(y = {\log _2}x\) như Hình 4. Từ đồ thị này, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to {0^ + }\) và tập giá trị của hàm số đã cho.
b) Lập bảng giá trị và vẽ đồ thị của hàm số \(y = {\log _{\frac{1}{2}}}x\). Từ đó, nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to {0^ + }\) và tập giá trị của hàm số này.
a:
i:
| x | 1/2 | 1 | 2 | 4 |
| y | -1 | 0 | 1 | 2 |
ii:
Hàm số liên tục và đồng biến trên \(\left(0;+\infty\right)\)
\(\lim\limits_{x\rightarrow+\infty}log_2x=+\infty;\lim\limits_{x\rightarrow0^+}log_2x=-\infty\)
Tập giá trị: R
b:
| x | 1/2 | 1 | 2 | 4 |
| y | 1 | 0 | -1 | -2 |
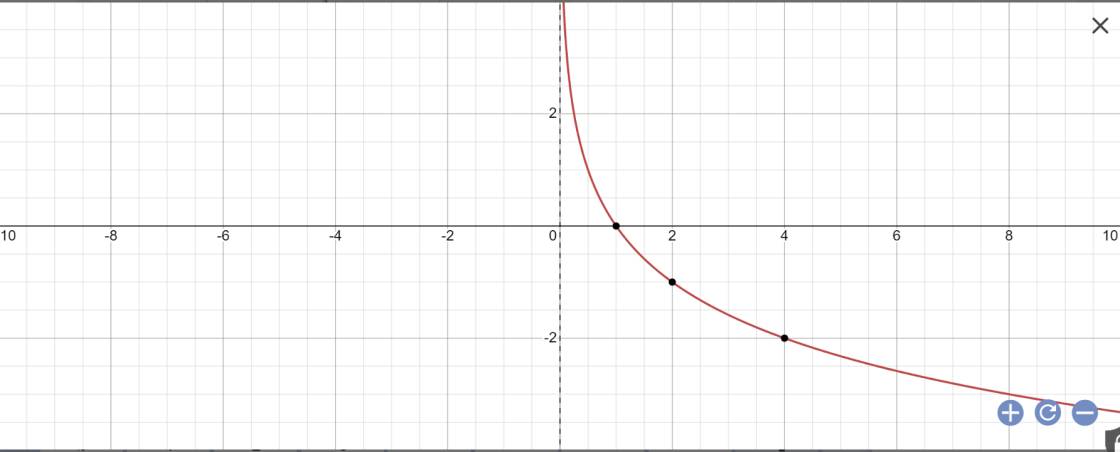
Hàm số liên tục và nghịch biến trên \(\left(0;+\infty\right)\)
\(\lim\limits_{x\rightarrow+\infty}log_{\dfrac{1}{2}}x=-\infty;\lim\limits_{x\rightarrow0^+}log_{\dfrac{1}{2}}x=+\infty\)
Tập giá trị: R
Tìm tập xác định của các hàm số sau:
a) \(y = \log \left| {x + 3} \right|;\)
b) \(y = \ln \left( {4 - {x^2}} \right).\)
a, \(y=log\left|x+3\right|\) có nghĩa khi \(\left|x+3\right|>0\)
Mà \(\left|x+3\right|\ge0\forall x\in R\)
\(\Rightarrow\) \(\left|x+3\right|>0\) khi \(x\ne-3\)
Vậy tập xác định của hàm số là D = R \ {-3}.
b, \(y=ln\left(4-x^2\right)\) có nghĩa khi \(4-x^2>0\)
\(\Rightarrow x^2< 4\\ \Leftrightarrow-2< x< 2\)
Vậy tập xác định của hàm số là D = (-2;2).
Giải các phương trình sau:
a) \({\left( {\frac{1}{4}} \right)^{x - 2}} = \sqrt 8 \);
b) \({9^{2x - 1}} = {81.27^x}\);
c) \(2{\log _5}\left( {x - 2} \right) = {\log _5}9\);
d) \({\log _2}\left( {3{\rm{x}} + 1} \right) = 2 - {\log _2}\left( {x - 1} \right)\).
\(a,\left(\dfrac{1}{4}\right)^{x-2}=\sqrt{8}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{2x-4}=\left(\dfrac{1}{2}\right)^{-\dfrac{3}{2}}\\ \Leftrightarrow2x-4=-\dfrac{3}{2}\\ \Leftrightarrow2x=\dfrac{5}{2}\\ \Leftrightarrow x=\dfrac{5}{4}\)
\(b,9^{2x-1}=81\cdot27^x\\ \Leftrightarrow3^{4x-2}=3^{4+3x}\\ \Leftrightarrow4x-2=4+3x\\ \Leftrightarrow x=6\)
c, ĐK: \(x-2>0\Rightarrow x>2\)
\(2log_5\left(x-2\right)=log_59\\
\Leftrightarrow log_5\left(x-2\right)^2=log_59\\
\Leftrightarrow\left(x-2\right)^2=3^2\\
\Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\\
\Leftrightarrow\left[{}\begin{matrix}x=5\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)
Vậy phương trình có nghiệm là x = 5.
d, ĐK: \(x-1>0\Leftrightarrow x>1\)
\(log_2\left(3x+1\right)=2-log_2\left(x-1\right)\\ \Leftrightarrow log_2\left(3x+1\right)\left(x-1\right)=2\\ \Leftrightarrow3x^2-2x-1=4\\ \Leftrightarrow3x^2-2x-5=0\\ \Leftrightarrow\left(3x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)
Vậy phương trình có nghiệm \(x=\dfrac{5}{3}\)
Hàm số nào sau đây đồng biến trên tập xác định của nó?
A. \(y = {\log _{0,5}}x\).
B. \(y = {{\rm{e}}^{ - x}}\).
C. \(y = {\left( {\frac{1}{3}} \right)^x}\).
D. \(y = \ln x\).
Chọn D. Bởi vì hàm số ln x luôn luôn dương nên chắc chắn sẽ đồng biến trên TXĐ của nó
Tính đạo hàm của các hàm số sau:
a) \(y = {\left( {2{x^3} + 3} \right)^2}\);
b) \(y = \cos 3x\);
c) \(y = {\log _2}\left( {{x^2} + 2} \right)\).
a, \(y=\left(2x^3+3\right)^2\)
\(y'=2\left(2x^3+3\right)6x^2\)
\(=12x^2\left(2x^3+3\right)\)
b,\(y=cos3x\)
\(y'=-3sin3x\)
c, \(y=log_2\left(x^2+2\right)\)
\(y'=\dfrac{2x}{\left(x^2+2\right)ln2}\)
tìm tập xác định của hàm số
a) \(y=log_2\left(x^2-16\right)\)
b) \(y=log_3\left(x^2-2x+1\right)\)
c) \(y=log_2\left(2-x\right)\left(x+1\right)\)
d) \(y=log\left(x^2-1\right)\left(X+5\right)\)
ĐKXĐ:
a.
\(x^2-16>0\Rightarrow\left[{}\begin{matrix}x>4\\x< -4\end{matrix}\right.\)
b.
\(x^2-2x+1>0\Rightarrow\left(x-1\right)^2>0\Rightarrow x\ne1\)
c.
\(\left(2-x\right)\left(x+1\right)>0\Rightarrow-1< x< 2\)
d.
\(\left(x^2-1\right)\left(x+5\right)>0\Rightarrow\left[{}\begin{matrix}-5< x< -1\\x>1\end{matrix}\right.\)
Tính đạo hàm của các hàm số sau:
a) \(y = \left( {{x^2} + 3x - 1} \right){e^x}\);
b) \(y = {x^3}{\log _2}x\).
a: \(y'=\left(x^2+3x-1\right)'\cdot e^x+\left(x^2+3x-1\right)\cdot\left(e^x\right)'\)
\(=e^x\left(2x+3\right)+\left(x^2+3x-1\right)\cdot e^x\)
\(=e^x\left(x^2+5x+2\right)\)
b: \(y'=\left(x^3\right)'\cdot log_2x+x^3\cdot\left(log_2x\right)'\)
\(=3x^2\cdot log_2x+x^3\cdot\dfrac{1}{x\cdot ln2}\)
Tìm tập xác định của các hàm số sau :
a) \(y=\dfrac{2}{\sqrt{4^x-2}}\)
b) \(y=\log_6\dfrac{3x+2}{1-x}\)
c) \(y=\sqrt{\log x+\log\left(x+2\right)}\)
d) \(y=\sqrt{\log\left(x-1\right)+\log\left(x+1\right)}\)