biểu diễn góc AOE = 30 độ trên đường tròn lượng giác
biểu diễn góc AOP = 270 độ trên đường tròn lượng giác
biểu diễn góc AOE = 30 độ trên đường tròn lượng giác
biểu diễn góc AOA' = -180 độ trên đường tròn lượng giác
Biểu diễn góc AOC = 60 độ và góc AOB = -150 độ trên đường tròn lượng giác
biểu diễn góc AOM = -45 độ trên đường tròn lượng giác
Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau: 2pi/3
Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo là:
a) \( - {1485^ \circ }\)
b) \(\frac{{19\pi }}{4}\)
a) Ta có \( - {1485^ \circ } = - {45^ \circ } + ( - 4){.360^ \circ }\). Vậy điểm biểu diễn góc lượng giác có số đo \( - {1485^ \circ }\)là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ IV sao cho \(\widehat {AMO} = {45^ \circ }\)
b) Ta có \(\frac{{19\pi }}{4} = \frac{{3\pi }}{4} + 4\pi \). Vậy điểm biểu diễn góc lượng giác có số đo \(\frac{{19\pi }}{4}\) là điểm N trên phần đường tròn lượng giác thuộc góc phần tư thứ II sao cho \(\widehat {AMO} = \frac{{3\pi }}{4}\).
Trong Hình 3, những điểm nào trên đường tròn lượng giác biểu diễn góc lượng giác x có \(cosx = \frac{{ - 1}}{2}\)? Xác định số đo của các góc lượng giác đó.
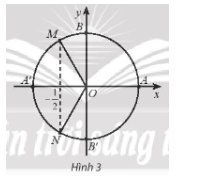
Điểm biểu diễn góc lượng giác x có \(cosx = \frac{{ - 1}}{2}\) là M và N.
Số đo góc lượng giác có điểm biểu diễn M là: \(\frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\).
Số đo góc lượng giác có điểm biểu diễn N là: \(\frac{{4\pi }}{3} + k2\pi ,k \in \mathbb{Z}\).
Cho góc lượng giác có số đo bằng \(\frac{{5\pi }}{6}\)
a) Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác đã cho.
b) Tính các giá trị lượng giác của góc lượng giác đã cho.
Tham khảo:
a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)
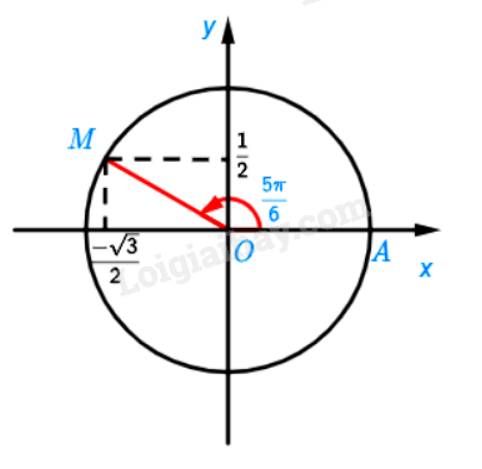
b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - 3}}{{\sqrt 3 }}\)
Biểu diễn các góc lượng giác \(\alpha = - \frac{{5\pi }}{6},\;\beta = \frac{\pi }{3},\;\gamma = \frac{{25\pi }}{3},\delta = \frac{{17\pi }}{3}\) trên đường tròn lượng giác. Các góc nào có điểm biểu diễn trùng nhau?
A. \(\beta \) và \( \gamma \)
B. \(\alpha, \beta, \gamma \)
C. \(\beta ,\gamma ,\delta \)
D. \(\alpha \) và \(\beta \),
Ta có: \(\frac{{25\pi }}{3} = \frac{\pi }{3} + 4.2\pi .\) Do đó điểm biểu diễn cung lượng giác \(\frac{{25\pi }}{3}\) trùng với điểm biểu diễn cung lượng giác \(\frac{\pi }{3}\).
Vậy ta chọn đáp án A
Góc lượng giác \(\frac{{31\pi }}{7}\) có cùng biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?
\(\frac{{3\pi }}{7};\,\,\frac{{10\pi }}{7};\,\,\frac{{ - 25\pi }}{7}\)
\(\dfrac{31\pi}{7}=\dfrac{3\pi}{7}+2\cdot2\pi\\ -\dfrac{25\pi}{7}=-\dfrac{4\pi}{7}-3\pi\\ \dfrac{10\pi}{7}=\dfrac{3\pi}{7}+\pi\)
\(\Rightarrow\dfrac{31\pi}{7}\) có cùng biểu diễn trên đường tròn lượng giác với góc \(\dfrac{3\pi}{7}\)