Chứng minh phương trình 2x3-9x2+12x-2-m=0 có 3 nghiệm dương phân biệt với mọi m thuộc (2;3)

Những câu hỏi liên quan
Hàm số y 2x3-9x2+ 12x có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình
2
x
3
-
9
x
2
+
12
x
+
m
0
có sáu nghiệm phân biệt. A.m - 5 B. -5 m- 4 C. 4 m 5 D.m -4
Đọc tiếp
Hàm số y= 2x3-9x2+ 12x có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình 2 x 3 - 9 x 2 + 12 x + m = 0 có sáu nghiệm phân biệt.
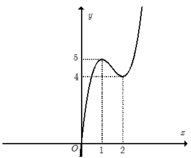
A.m< - 5
B. -5< m<- 4
C. 4< m< 5
D.m> -4
+Trước tiên từ đồ thị hàm số y= 2x3- 9x2+12x , ta suy ra đồ thị hàm số y= 2 x 3 - 9 x 2 + 12 x như hình dưới đây:
+ Phương trình 2 x 3 - 9 x 2 + 12 x + m = 0 và đường thẳng y= -m
+ Dựa vào đồ thị hàm số y = 2 x 3 - 9 x 2 + 12 x , yêu cầu bài toán trở thành:
4< -m< 5 hay -5<m< -4.
Chọn B.
Đúng 0
Bình luận (0)
Hình vẽ dưới đây là đồ thị của hàm số
y
2
x
3
-
9
x
2
+
12
x
-
4
. Giá trị của m để phương trình
2
x
3
-
9
x
2
+
12
x
m
có 6 nghiệm phân biệt là: A. 0 m 1 B. 4 m 5...
Đọc tiếp
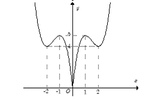
Hình vẽ dưới đây là đồ thị của hàm số y = 2 x 3 - 9 x 2 + 12 x - 4 . Giá trị của m để phương trình 2 x 3 - 9 x 2 + 12 x = m có 6 nghiệm phân biệt là:
A. 0 < m < 1
B. 4 < m < 5
C. 0 < m < 4
D. 1 < m < 5
Đặt y = 2 x 3 - 9 x 2 + 12 x - 4
Ta có f x = f x , x ≥ 0 f - x , x < 0 .
Do f x là hàm số chẵn nên đồ thị đối xứng qua trục tung. Như vậy đồ thị của nó gồm hai
Phần bên phải trục tung của đồ thị hàm số y = f(x)
Đối xứng phần đồ thị trên qua trục tung
Ta có: 2 x 3 - 9 x 2 + 12 x = m
⇔ 2 x 3 - 9 x 2 + 12 x - 4 = m - 4
Phương trình đã cho có 6 nghiệm phân biệt.
Đường thẳng y = m - 4 cắt đồ thị f x hàm số tại 6 điểm phân biệt
0 < m - 4 < 1 nên 4 < m < 5
Đáp án B
Đúng 0
Bình luận (0)
Cho phương trình : x^2 - 2(m+1)x + 2m = 0
a) Chứng minh phương trình luôn có 2 nghiệm phân biệt với mọi m
b) Tìm các giá trị của m để phương trình có 2 nghiệm phân biệt cùng dương
c) Tìm hệ thức liên hệ giữa 2 nghiệm không phụ thuộc m
Cho phương trình x2-mx+m-1=0.
giải phương trình với m=3
chứng minh phương trình có nghiệm với mọi m
Cho phương trình x2-2mx+m=7. chứng minh phương trình có 2 nghiệm phân biệt với mọi m
`@` Thay `m=3` vào ptr có: `x^2-3x+3-1=0<=>x^2-3x+2=0`
Ptr có: `a+b+c=1-3+2=0=>x_1 =1;x_2=-2`
`@` Ptr có: `\Delta=(-m)^2-4m+4=m^2-4m+4=(m-2)^2 >= 0` (Luôn đúng `AA m`)
`=> AA m` ptr luôn có nghiệm.
______________________________
`x^2-2mx+m=7<=>x^2-2mx+m-7=0`
Ptr có: `\Delta'=(-m)^2-m+7=m^2-m+7=(m-1/2)^2+27/4 > 0 AA m`
`=>` Ptr có `2` nghiệm pb `AA m`
Đúng 2
Bình luận (0)
Tìm m để phương trình có 2 nghiệm:
2
x
3
-
9
x
2
+
12
x
m
B.
4
m
5
C.
m
5
D.
m
0
Đọc tiếp
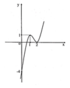
Tìm m để phương trình có 2 nghiệm: 2 x 3 - 9 x 2 + 12 x = m
B. 4 < m < 5
C. m = 5
D. m = 0
Cho phương trình 9 x 2 + 2 ( m 2 - 1 ) x + 1 = 0 . Chứng tỏ rằng với m > 2 phương trình có hai nghiệm phân biệt âm.
Chứng minh phương trình sau có ít nhất 2 nghiệm phân biệt Với mọi m thuộc R. đặt f(x)=X^4+(m-2)x^3+x^3+(3m+1)x-4m-2016=0
Cho phương trình \(x^2-2\left(m-1\right)x+m-3=0\). Chứng minh phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m
Xét pt cho là pt bậc hai một ẩn $x$ ( Với $a=1 \neq 0, b=-2(m-1), c = m-3$ )
Ta có : \(\Delta'=b'^2-ac\)
\(=\left[-\left(m-1\right)\right]^2-\left(m-3\right)\cdot1\)
\(=m^2-2m+1-m+3\)
\(=m^2-3m+4=\left(m-\dfrac{3}{2}\right)^2+\dfrac{7}{4}>0\)
Nên pt cho luôn có hai nghiệm phân biệt \(\forall m\)
Đúng 2
Bình luận (0)
Phương trình
x
3
-
12
x
+
m
-
2
0
có ba nghiệm phân biệt với m thuộc khoảng A.
-
18 m 14 B.
-
4 m 4 C.
-
14 m 18 D.
-
16 m 16
Đọc tiếp
Phương trình x 3 - 12 x + m - 2 = 0 có ba nghiệm phân biệt với m thuộc khoảng
A. - 18 < m < 14
B. - 4 < m < 4
C. - 14 < m < 18
D. - 16 < m < 16
Đáp án A
Phương pháp: Sử dụng sự tương giao giữa hai đồ thị hàm số để đánh giá số nghiệm của phương trình.
Cách giải: ![]()
Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị hàm số ![]() và đường thẳng
và đường thẳng ![]()
Xét ![]() có
có ![]()
Bảng biến thiên:
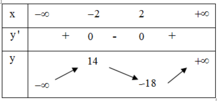
Khi đó, ![]() cắt
cắt ![]() tại 3 điểm phân biệt
tại 3 điểm phân biệt ![]()
Đúng 0
Bình luận (0)













