Hình thang vuông ABCD có A = D = 90°, AB = AD =4 cm, DC = 8cm. Tính các góc hình thang
Những câu hỏi liên quan
hình thang vuông ABCD có góc A=góc D=90 độ , AB =AD =2 cm , DC=4 cm . tính các góc của hình thang.
hình thang vuông ABCD có góc A bằng góc D và bằng 90 độ, AB = AD = 2cm, DC = 4cm. Tính các góc của hình thang
Cho hình thang vuông ABCD có góc A =góc D=90 độ . AD=4 cm; DC=9cm;Ab=1/3 CD.
a)Tính diện tích hình thang ABCD
b)Kéo dài AD cắt Cb tại M.TÍnh diện tích tam giác ABM
diện tích hình thang abcd
theo công thức S=1/2h(a+b)
có ab=3cm(ab=1/3CD);Ad=4cm(Ad là chiều cao);DC=9cm
suy ra: S= 1/2 nhân 4(3+9)=24
Đúng 1
Bình luận (0)
Cho hình thang vuông ABCD có
A
^
D
^
90
°
, AB AD 2cm, DC 4cm. Tính góc ABC của hình thang. A.
137
°
B.
136
°
C.
36
°
D.
135
°
Đọc tiếp
Cho hình thang vuông ABCD có A ^ = D ^ = 90 ° , AB = AD = 2cm, DC = 4cm. Tính góc ABC của hình thang.
A. 137 °
B. 136 °
C. 36 °
D. 135 °
Đáp án cần chọn là: D
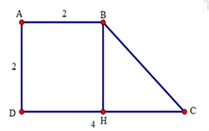
Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.
Lại có B H C ^ = 90 ° (do BH ⊥ CD) nên tam giác BHC vuông cân tại H.
Do đó B C H ^ = 180 ° - B H C ^ ÷ 2 = 180 ° - 90 ° ÷ 2 = 45 °
Xét hình thang ABCD có:
A B C ^ = 360 ° - A ^ + D ^ + C ^ = 360 ° - 90 ° + 90 ° + 45 ° = 135 °
Vậy A B C ^ = 135 ° .
Đúng 3
Bình luận (0)
cho hình thang vuông ABCD . có A=D=90 độ . Cạnh AD= 77 cm AB =91cm. DC=127cm .
a, tính diện tích hình thang
b, tính góc C va cạnh BC
Cho hình thang ABCD có góc A = góc D = 90 độ . AD = 77 cm , AB = 91 cm , DC = 127 cm .
a. Tính diện tích hình thang ABCD
b. Tính góc C và BC
9 tháng 10 2021 lúc 20:16
Cho hình thang ABCD có góc A = góc D = 90 độ . AD = 77 cm , AB = 91 cm , DC = 127 cm .
a. Tính diện tích hình thang ABCD
b. Tính góc C và BC
9 tháng 10 2021 lúc 20:02
Cho hình thang ABCD có góc A = góc D = 90 độ . AD = 77 cm , AB = 91 cm , DC = 127 cm .
a. Tính diện tích hình thang ABCD
b. Tính góc C và BC
Cho hình thang vuông ABCD có góc A=góc D=90 độ,AB=AD=1/2DC
a)Tính các góc của hình thang
b)CM AC vuông góc CD
c)Tính chu vi hình thang nếu AB=3cm
(vẽ hình hộ)
a: Kẻ BH vuông góc CD
Xét tứ giác ABHD có
góc BAD=góc ADH=góc BHD=90 độ
AB=AD
=>ABHD là hình vuông
=>BH=HD=AB=DC/2
=>góc BDH=45 độ
DH=DC/2
=>H là trung điểm của DC
Xét ΔBDC có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBDC cân tại B
=>góc C=45 độ
=>góc ABC=135 độ
c: DC=2*3=6cm
AD=AB=3cm
BC=căn 3^2+3^2=3*căn 2cm
C=6+3+3+3căn 2=12+3căn 2(cm)
Đúng 1
Bình luận (0)