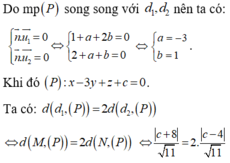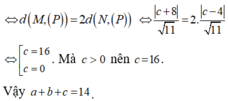y x A y 105 độ B 75 x z Chứng tỏ yy// Bz bằng 2 cách
Đọc tiếp
Chứng tỏ yy'// Bz bằng 2 cách
Những câu hỏi liên quan
Trong không gian Oxyz, cho hai đường thẳng
d
1
:
x
-
1
1
y
+
2
1
z
-
1
2
và
d...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y + 2 1 = z - 1 2
và d 2 : x - 1 2 = y - 1 1 = z + 2 1 . Mặt phẳng (P) : x + ay + bz + c = 0 song song
với d 1 , d 2 và khoảng cách từ d 1 đến (P) bằng 2 lần khoảng cách từ d 2 đến (P).
Giá trị của a + b + c bằng
A. 6
B. 14
C. -4
D. -6
30 tháng 8 2023 lúc 9:03
Cho hình vẽ:
45* 135* 75* 30* A x B C y z
a, Chứng tỏ rằng Ax // By b, Chứng minh By // Cz
Đọc tiếp
Cho hình vẽ:
a, Chứng tỏ rằng Ax // By b, Chứng minh By // Cz
a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz
Đúng 0
Bình luận (0)
1) cho dãy tỉ số bằng nhau :x/a+2b+c = y/2a+b-c = z/4a-4b+c
chứng minh : a/x+2y+z = b/2x+y-z = c/4x-4y+z ( các tỉ số đều có nghĩa)
2) cho bz - cy/a = cx - az/b = ay - bx/c
chứng minh x/a = y/b = z/c
làm hộ mk vs , mk tick cho!!
Tìm x,y,z biết:
a) x(x+y+z)=45 ; y(x+y+z)= 75 ; z(x+y+z)=105
b) 1+3y/12 = 1+5y / 5x = 1+7y / 4x
Cho yc-bz/x=za-xc/y=xb-ya/z với(x,y,z khác o).Chứng minh a/x=b/y=c/z
cho 2 đth yy'//xx', đth tt' cắt xx' tại A và yy' tại B. Kẻ tia phân giác Az của x'AB, Tía phân giác Bz' của ABy. Chứng tỏ Az//.Bz
Ta có: yy'//xx' nên yBA=BAx'
suy ra z'BA=BAz (vi Bz' va Az lần lượt là phân giác của yBA và BAx') mà chúng ở vị trí so le trong nên Bz'//Az ( đpcm)
Đúng 0
Bình luận (0)
a, chứng tỏ rằng alớn hơn hoặc bằng b, thì:
(ax + by)(bx+ay)lớn hơn hoặc bằng (a+b)2 nhân xy
b, với x,y,z>0 chứng mình rằng
(x+y+z)(1/x+1/y+1/z0lowsn hơn hặc bằng 9
cho \(\dfrac{cy-bz}{x}=\dfrac{az-cx}{y}=\dfrac{bx-ay}{z}\) chứng minh rằng :\(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)
Ta có :
\(\dfrac{cy-bx}{x}=\dfrac{az-cx}{y}=\dfrac{bx-ay}{z}=\dfrac{bxz-cxy+cxy-ayz+ayz-bxz}{ax+by+cz}=0\)
\(\Rightarrow\dfrac{cy-bz}{x}=0\) \(\Rightarrow cy=bz\) \(\Rightarrow\) \(\dfrac{b}{y}=\dfrac{c}{z}\left(1\right)\)
\(\Rightarrow\dfrac{az-cx}{y}=0\) \(\Rightarrow az=cx\) \(\Rightarrow\dfrac{a}{x}=\dfrac{c}{z}\left(2\right)\)
Từ (1) và (2) suy ra : \(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)
Đúng 2
Bình luận (0)
Cho a,b,c,x,y,z khác 0 thỏa mãn bx = ay ; cy = bz
Chứng minh rằng :
\(\frac{a^2}{x}+\frac{b^2}{y}+\frac{c^2}{z}=\frac{\left(a+b+c\right)^2}{x+y+z}\)
giúp mình!!
(a+b+c)\(^2\) đây la hang đang thuc nâng cao e co muôn khai triên ra k ??
Đúng 0
Bình luận (0)
\(=a^2+b^2+c^2+2ab+2ac+2bc\)
đây e nghi ra cach lam đi
Đúng 0
Bình luận (0)