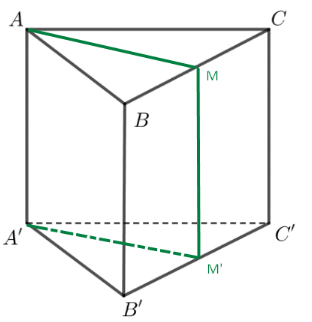
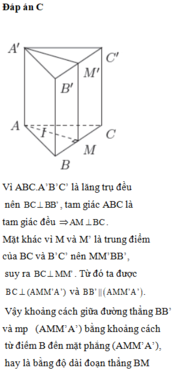
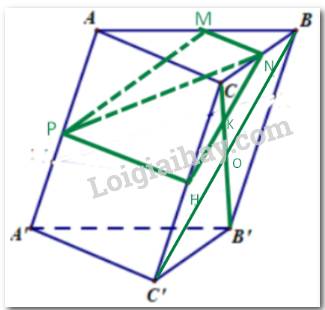
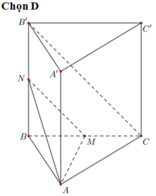
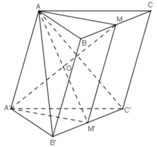
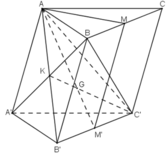
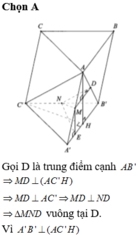
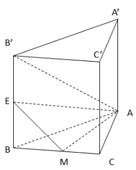
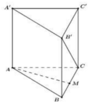
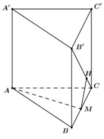
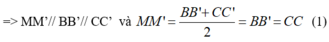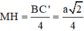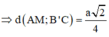Cho hình lăng trụ tam giác ABC.A’B’C’. Lấy M, M’ lần lượt là trung điểm các đoạn thẳng BC, B’C’; lấy các điểm G, G’, K lần lượt thuộc các đoạn AM, A’M’, A’B sao cho `(AG)/(AM)=(A′G′)/(A′M′)=(A′K)/(A′B)=23`
a) Chứng minh rằng CM’ // (A’BM’)
b) Chứng minh rằng G’K // (BCC’B’)
c) Chứng minh rằng (GG’K) // (BCC’B’)
d) Gọi(α)
là mặt phẳng đi qua K và song song với mặt phẳng (ABC). Mặt phẳng(α)
cắt cạnh CC’ tại điểm I. Tính `(IC)/(IC′)`