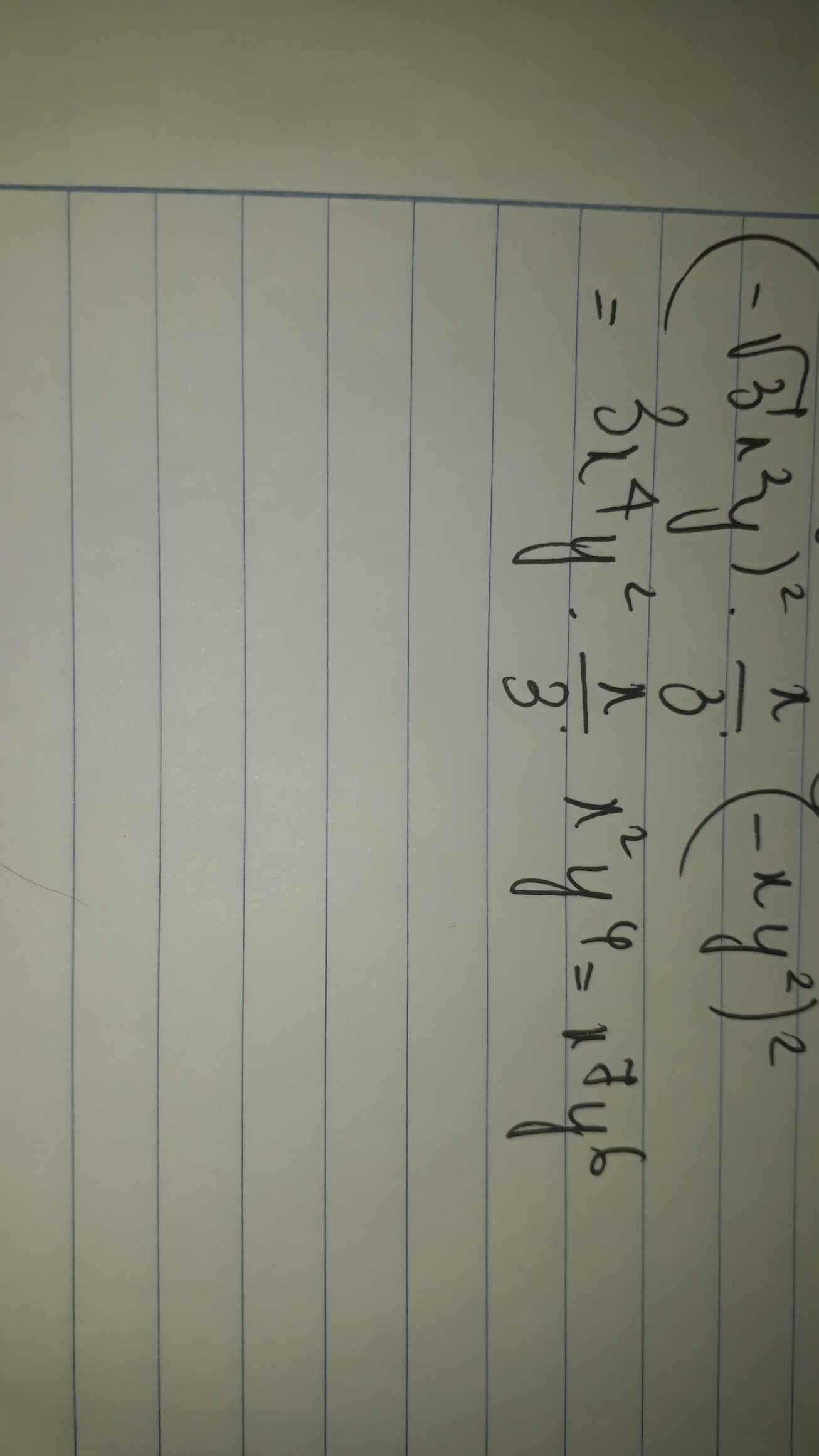x mũ n nhân y mũ n +2 nhân (xy+x mũ 2 y +1)

Những câu hỏi liên quan
Cho hai đơn thức A= (-2 phần 5 nhân x mũ 2 nhân y) nhân (15 phần 8 nhân x nhân y mũ 2) (-x mũ 3 nhân y mũ 2) ;B= (xy) mũ 2 nhân 5 phần 8 nhân x mũ 2 nhân y mũ 3
a)Thu gọn đơn thức A, đơn thức B
b) Xđịnh hệ số , phần biến và bậc của mỗi đơn thức
phân tích đa thức sau thành nhân tử
k, 2x mũ 2 - x - 6xy + 3y
l, x mũ 2 - xy + 5x - 5y
m, (( a mũ 2 + 4 ) mũ 2 - 16a mũ 2
n, x mũ 2 y mũ 2 + 1 - x mũ 2 - y mũ 2
q, 3x mũ 2 - 6xy + 3y mũ 2 - 12z mũ 2
k) = x( 2x - 1 ) - 3y( 2x - 1 ) = ( 2x - 1 )( x - 3y )
l) = x( x - y ) + 5( x - y ) = ( x - y )( x + 5 )
m) = ( a2 - 4a + 4 )( a2 + 4a + 4 ) = ( a - 2 )2( a + 2 )2
n) = y2( x2 - 1 ) - ( x2 - 1 ) = ( x - 1 )( x + 1 )( y - 1 )( y + 1 )
q) = 3[ ( x - y )2 - 4z2 ] = 3( x - y - 2z )( x - y + 2z )
Tìm x,y thuộc N biết 3 mũ x + 89 = (2 mũ y + 1) nhân ( 2 mũ y + 2)
Câu hỏi của Garena Liên quân mobile - Toán lớp 6 - Học toán với OnlineMath
x mũ n y mũ n+2(xy+x mũ 2 y +1)
x\(^{n+1}\)y\(^{n+1}\)+2xy+x\(^{ }\)\(^{n+2}\)y\(\)\(^{n+1}\)+2x\(^2\)y+x\(^n\)y\(^n\)+2
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử
a,-3xy mũ 2+ x mũ 2y mũ 2-5x mũ 2y
b,x mũ 2(x+1)-(x+1)
C, y mũ 2+ xy+ y
d,4x(x-2)-(x-2)
,
b)x2(x+1)-(x+1)=(x+1)(x2-1)
d) 4x(x-2)-(x-2)=(x-2)(4x-1)
câu a bn ghi mik k hỉu
Đúng 1
Bình luận (0)
bài 2; phân tích đa thức sau thành nhân tử
a, x mũ 2 + 7x + 7y - y mũ 2
b, x mũ 2 - 2x - 9y mũ 2 + 6y
c, x mũ 2 - xy +x mũ 3 - 3x mũ 2 y + 3x mũ 2 y - y mũ 3
\(a,x^2+7x+7y-y^2\)
\(=x^2-y^2+7\left(x+y\right)\)
\(=\left(x-y\right)\left(x+y\right)+7\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y+7\right)\)
\(b,x^2-2x-9y^2+6y\)
\(=x^2-\left(3y\right)^2-2\left(x-3y\right)\)
\(=\left(x-3y\right)\left(x+3y\right)-2\left(x-3y\right)\)
\(=\left(x-3y\right)\left(x+3y-2\right)\)
\(c,x^2-xy+x^3-3x^{2y}+3x^{2y}-y^3\)
\(=x\left(x-y\right)+\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=\left(x-y\right)\left(x+x^2+xy+y^2\right)\)
Bài 1: Nhân các đơn thức sau và tìm bậc và hệ số của đơn thức nhận được .
a,(-2x mũ 2.y ).(5.x.y mũ 4 )
b, (27 phần 10 .x mũ 4. y mũ 2 ).(5 phần 9.x.y )
c, (1 phần 3 .x mũ 3.y).(-xy)mũ 2
a/ \(\left(-2x^2y\right)5xy^4\)
\(=-10x^3y^5\)
Đúng 1
Bình luận (0)
a) Ta có: \(\left(-2x^2y\right)\cdot\left(5xy^4\right)\)
\(=\left(-2\cdot5\right)\cdot\left(x^2\cdot x\right)\cdot\left(y\cdot y^4\right)\)
\(=-10x^3y^5\)
b) Ta có: \(\left(\dfrac{27}{10}x^4y^2\right)\cdot\left(\dfrac{5}{9}xy\right)\)
\(=\left(\dfrac{27}{10}\cdot\dfrac{5}{9}\right)\cdot\left(x^4\cdot x\right)\cdot\left(y^2\cdot y\right)\)
\(=\dfrac{3}{2}x^5y^3\)
c) Ta có: \(\left(\dfrac{1}{3}x^3y\right)\cdot\left(-xy\right)^2\)
\(=\dfrac{1}{3}x^3y\cdot x^2y^2\)
\(=\dfrac{1}{3}x^5y^3\)
Đúng 1
Bình luận (0)
phân tích đa thức sau thành nhân tử
t, x mũ 2 y - xy mũ 2 + x mũ 3 - y mũ 3
o, 4x mũ 2 - 25 + ( 2x + 7 )( 5 - 2x )
p, 5x mũ 2 - 5y mũ 2 - 10x + 10y
r, x mũ 2 - xy + 4x - 2y + 4
a)x²−2x−4y²−4ya)x²-2x-4y²-4y
=x²−2x−4y²−4y+2xy−2xy=x²-2x-4y²-4y+2xy-2xy
=(x²−2xy−2x)+(2xy−4y²−4y)=(x²-2xy-2x)+(2xy-4y²-4y)
=x(x−2y−2)+2y(x−2y−2)=x(x-2y-2)+2y(x-2y-2)
=(x+2y)(x−2y−2)=(x+2y)(x-2y-2)
b)x4+2x³−4x−4b)x4+2x³-4x-4
=x4+2x³+2x²−2x²−4x−4=x4+2x³+2x²-2x²-4x-4
=(x4+2x³+2x²)−(2x²+4x+4)=(x4+2x³+2x²)-(2x²+4x+4)
=x²(x²+2x+2)−2(x²+2x+2)=x²(x²+2x+2)-2(x²+2x+2)
=(x²−2)(x²+2x+2)=(x²-2)(x²+2x+2)
c)x³+2x²y−x−2yc)x³+2x²y-x-2y
=x²(x+2y)−(x+2y)=x²(x+2y)-(x+2y)
=(x²−1)(x+2y)=(x²-1)(x+2y)
=(x+1)(x−1)(x+2y)=(x+1)(x-1)(x+2y)
d)3x²−3y²−2(x−y)²d)3x²-3y²-2(x-y)²
=3(x²−y²)−2(x−y)²=3(x²-y²)-2(x-y)²
=3(x+y)(x−y)−2(x−y)²=3(x+y)(x-y)-2(x-y)²
=(x−y)[3(x+y)−2(x−y)]=(x-y)[3(x+y)-2(x-y)]
=(x−y)(3x+3y−2x+2y)=(x-y)(3x+3y-2x+2y)
=(x−y)(x+5y)=(x-y)(x+5y)
e)x³−4x²−9x+36e)x³-4x²-9x+36
=(x³−4x²)−(9x−36)=(x³-4x²)-(9x-36)
=x²(x−4)−9(x−4)=x²(x-4)-9(x-4)
=(x−4)(x²−9)=(x-4)(x²-9)
=(x−4)(x²−3²)=(x-4)(x²-3²)
=(x−4)(x+3)(x−3)=(x-4)(x+3)(x-3)
f)x²−y²−2x−2yf)x²-y²-2x-2y
=(x²−y²)−(2x+2y)=(x²-y²)-(2x+2y)
=(x+y)(x−y)−2(x+y)=(x+y)(x-y)-2(x+y)
=(x+y)(x−y−2)
hok tốt nhé
k đi
(âm căn 3 nhân x mũ 2 nhân y )mũ 2 nhân (x phần 3) nhân (âm x nhân y mũ 2) mũ 2
\(\left(-\sqrt{3x^2y}\right)^2.\dfrac{x}{3}.\left(-xy^2\right)^2\\ =3x^2y.\dfrac{x}{3}.x^2y^4\\ =x^5y^5\)
Đúng 0
Bình luận (0)