cho hình bình hành có góc tù 120 độ có cạnh bằng 3 tính vectơ BD và vectơ AC

Những câu hỏi liên quan
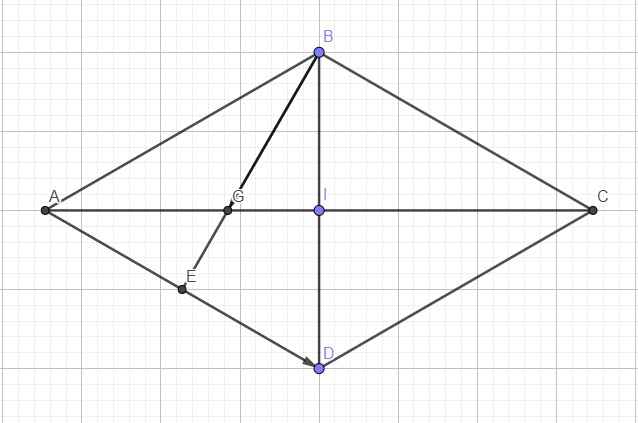
Cho hình thoi ABCD tâm O có cạnh bằng 2a và góc ABC =120 độ. Gọi G là trọng tâm tam giác ABD, tính độ dài của vectơ BG + vectơ AD
Cho hình thoi ABCD tâm O có cạnh bằng 2a và góc ABC =120 độ. Gọi G là trọng tâm tam giác ABD, tính độ dài của vectơ BG + vectơ AD
\(\widehat{ABC}=120^0\Rightarrow\widehat{DAB}=180^0-120^0=60^0\)
\(\Rightarrow\Delta ABD\) đều
Gọi E là trung điểm AD \(\Rightarrow\overrightarrow{BE}=\dfrac{1}{2}\overrightarrow{BD}+\dfrac{1}{2}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BE}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}+\overrightarrow{AD}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}=\dfrac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{AD}\right)+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}\)
\(=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{4}{3}\overrightarrow{AD}=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\)
Đặt \(\overrightarrow{u}=\overrightarrow{BG}+\overrightarrow{AD}\Rightarrow\left|\overrightarrow{u}\right|^2=\left(-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\right)=\dfrac{4}{9}AB^2+\dfrac{16}{9}AD^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AD}\)
\(=\dfrac{4}{9}.4a^2+\dfrac{16}{9}4a^2-\dfrac{16}{9}.2a.2a.cos60^0=\dfrac{16}{3}a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=\dfrac{4a\sqrt{3}}{3}\)
Đúng 2
Bình luận (0)
Cho hình bình hành ABCD có O = AC n BD a,Tìm các vectơ khác vectơ O + Cùng phương với vectơ OA + Cùng chiều với vectơ BD b, Tìm các vectơ + bằng với AB + bằng với CO
Cho hình thoi tâm có cạnh bằng 2a và góc ABC=120 độ . Gọi G là trọng tâm tam giác , tính độ dài của vectơ BG + AD
1. Cho hình vuông ABCD cạnh a. Tính độ dài vectơ v= vectơ AC+ vectơ BD
2. Cho hình vuông tâm O cạnh a. Tính độ dài vectơ v= vectơ OA+ vectơ DC
cho hình bình hành ABCD có AB bằng 20cm ad bằng 15 cm , góc tạo bởi hai cạnh AB và BD là 120 độ .Tính diện tích hình bình hành ABCD
Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo và AB = a, BC = 3a.
a) Tính độ dài các vectơ \(\overrightarrow {AC} ,\overrightarrow {BD} \)
b) Tìm trong hình ảnh vectơ đối nhau và có độ dài bằng \(\frac{{a\sqrt {10} }}{2}\)
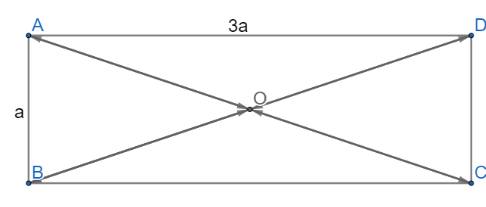
a) Ta có:
\(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {{\left( {3a} \right)}^2}} = a\sqrt {10} \)
+) \(\left| {\overrightarrow {AC} } \right| = AC = a\sqrt {10} \)
+) \(\left| {\overrightarrow {BD} } \right| = BD = a\sqrt {10} \)
b) O là giao điểm của hai đường chéo nên ta có:
\(AO = OC = BO = OD = \frac{{a\sqrt {10} }}{2}\)
Dựa vào hình vẽ ta thấy AO và CO cùng nằm trên một đường thẳng; BO và DO cùng nằm trên một đường thẳng
Suy ra các cặp vectơ đối nhau và có độ dài bằng \(\frac{{a\sqrt {10} }}{2}\) là:
\(\overrightarrow {OA} \) và \(\overrightarrow {OC} \); \(\overrightarrow {AO} \) và \(\overrightarrow {CO} \); \(\overrightarrow {OB} \) và \(\overrightarrow {OD} \); \(\overrightarrow {BO} \) và \(\overrightarrow {DO} \)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD tâm O có độ dài cạnh =6. Gọi E là điểm trên đường thẳng AC thỏa vectơ AC=3 vectơ AE và M là trung điểm AD. Chứng minh đẳng thức vectơ EB+vectơ EC+vectơ ED= vectơ AC
Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài các vectơ sau:
a) \(\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} ;\)
b) \(\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} .\)
a) \(\begin{array}{l}\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} = \left( {\overrightarrow {AC} + \overrightarrow {CB} } \right) + \overrightarrow {BD} \\ = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD}\\ \Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AD} } \right| = AD = 1\end{array}\)
b) \(\begin{array}{l}\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {AD} + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC} + \overrightarrow {AA} = \overrightarrow {AC} + \overrightarrow 0 = \overrightarrow {AC} \end{array}\)
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
\(\Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AC} } \right| = \sqrt 2 \)
Đúng 0
Bình luận (0)