Độ dài ACACAC được tính từ góc A=6∘A = 6^\circA=6∘ và cạnh đối AH=305 mAH = 305 \, mAH=305m.

AC=AHsin⁡A=305sin⁡6∘AC = \frac{AH}{\sin A} = \frac{305}{\sin 6^\circ}AC=sinAAH​=sin6∘305​

Độ dài CBCBCB được tính từ góc B=4∘B = 4^\circB=4∘ và cạnh đối HB=458 mHB = 458 \, mHB=458m.

CB=HBsin⁡B=458sin⁡4∘CB = \frac{HB}{\sin B} = \frac{458}{\sin 4^\circ}CB=sinBHB​=sin4∘458​

Thời gian leo dốc từ AAA đến CCC:

tAC=AC4 km/ht_{AC} = \frac{AC}{4 \, km/h}tAC​=4km/hAC​

Thời gian xuống dốc từ CCC đến BBB:

tCB=CB19 km/ht_{CB} = \frac{CB}{19 \, km/h}tCB​=19km/hCB​
 Tổng thời gian di chuyển: ttotal=tAC+tCBt_{\text{total}} = t_{AC} + t_{CB}ttotal​=tAC​+tCB​Thời gian bạn Học đến trường bằng cách cộng tổng thời gian này vào thời gian khởi hành 6 giờ 45 phút.

a: ta có: BC=BH+CH

=>BC=3,6+6,4=10(cm)

Xét ΔABC vuông tại A có AH là đường cao

nên \(HA^2=HB\cdot HC=3,6\cdot6,4=23,04=4,8^2\)

=>HA=4,8(cm)

ΔHAC vuông tại H

=>\(HA^2+HC^2=AC^2\)

=>\(AC^2=4,8^2+6,4^2=64=8^2\)

=>AC=8(cm)

Xét ΔABC vuông tại A có \(\sin B=\frac{AC}{BC}=\frac{8}{10}=\frac45\)

nên \(\hat{B}\) ≃53 độ

ΔABC vuông tại A

=>\(\hat{ABC}+\hat{ACB}=90^0\)

=>\(\hat{ACB}=90^0-53^0=37^0\)

b: Xét ΔAHB vuông tại H có HM là đường cao

nên \(AM\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HN là đường cao

nên \(AN\cdot AC=AH^2\left(2\right)\)

Từ (1),(2) suy ra \(AM\cdot AB=AN\cdot AC\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(HB\cdot HC=AH^2\) (4)

Xét tứ giác AMHN có \(\hat{AMH}=\hat{ANH}=\hat{MAN}=90^0\)

nên AMHN là hình chữ nhật

=>\(HA^2=HM^2+HN^2\) (3)

Xét ΔHAB vuông tại H có HM là đường cao

nên \(HM^2=MA\cdot MB\) (5)

Xét ΔHAC vuông tại H có HN là đường cao

nên \(HN^2=NA\cdot NC\left(6\right)\)

Từ (3),(4),(5),(6) suy ra \(HB\cdot HC=MA\cdot MB+NA\cdot NC\)

c: Ta có: AK⊥MN

=>\(\hat{KAC}+\hat{ANM}=90^0\)

mà \(\hat{ANM}=\hat{AHM}\) (AMHN là hình chữ nhật)

và \(\hat{AHM}=\hat{B}\left(=90^0-\hat{HAB}\right)\)

nên \(\hat{KAC}+\hat{B}=90^0\)

mà \(\hat{KCA}+\hat{B}=90^0\)

nên \(\hat{KAC}=\hat{KCA}\)

=>KA=KC

Ta có: \(\hat{KAC}+\hat{KAB}=\hat{BAC}=90^0\)

\(\hat{KCA}+\hat{KBA}=90^0\) (ΔABC vuông tại A)

mà \(\hat{KAC}=\hat{KCA}\)

nên \(\hat{KAB}=\hat{KBA}\)

=>KA=KB

mà KA=KC

nên KB=KC

=>K là trung điểm của BC

Câu 84:

$\sin 3x+2\cos ^2x=1$

$\sin 3x=1-2\cos ^2x=-\cos 2x=\sin (2x-\frac{\pi}{2})$

\(\Rightarrow \left[\begin{matrix} 3x=2x-\frac{\pi}{2}+2k\pi\\ 3x=\frac{3}{2}\pi-2x+2k\pi\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=(2k+\frac{3}{2})\pi\\ x=\frac{2k+\frac{3}{2}}{5}\pi\end{matrix}\right.\) với $k$ nguyên 

Nghiệm âm lớn nhất của pt:

$x=\frac{2(-1)+\frac{3}{2}}{5}\pi =\frac{-\pi}{10}$

84.

\(sin3x+2cos^2x=1\)

\(\Leftrightarrow sin3x+cos2x=0\)

\(\Leftrightarrow cos\left(\dfrac{\pi}{2}-3x\right)+cos2x=0\)

\(\Leftrightarrow2cos\left(\dfrac{\pi}{4}-\dfrac{x}{2}\right).cos\left(\dfrac{\pi}{4}-\dfrac{5x}{2}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos\left(\dfrac{\pi}{4}-\dfrac{x}{2}\right)=0\\cos\left(\dfrac{\pi}{4}-\dfrac{5x}{2}\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{4}-\dfrac{x}{2}=\dfrac{\pi}{2}+k\pi\\\dfrac{\pi}{4}-\dfrac{5x}{2}=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{2}-k2\pi\\x=-\dfrac{\pi}{10}-\dfrac{k2\pi}{5}\end{matrix}\right.\)

\(x=-\dfrac{\pi}{2}-k2\pi< 0\Leftrightarrow k>-\dfrac{1}{4}\Rightarrow k=0\Rightarrow x=-\dfrac{\pi}{2}\)

\(x=-\dfrac{\pi}{10}-k2\pi< 0\Leftrightarrow k>-\dfrac{1}{20}\Rightarrow k=0\Rightarrow x=-\dfrac{\pi}{10}\)

Vậy \(x=-\dfrac{\pi}{10}\) là nghiệm âm lớn nhất

Câu 85:

ĐKXĐ: $\cos 2x; \cos 3x\neq 0$

$\tan 2x\tan 3x=1$
$\Leftrightarrow \sin 2x\sin 3x=\cos 2x\cos 3x$
$\Leftrightarrow 2\sin 2x\sin 3x=2\cos 2x\cos 3x$

$\Leftrightarrow \cos 5x+\cos x=\cos x-\cos 5x$

$\Leftrightarrow 2\cos 5x=0$

$\Leftrihgtarrow \cos 5x=0$

$\Leftrightarrow x=\frac{1}{5}(\frac{\pi}{2}+k\pi$

$=\frac{2k+1}{10}\pi$

Nghiệm âm lớn nhất: $\frac{-2+1}{10}\pi =\frac{-\pi}{10}$

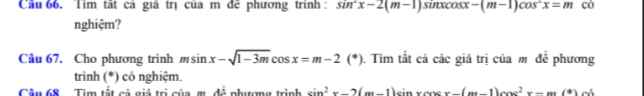
ĐKXĐ: \(1-3m\ge0\Rightarrow m\le\dfrac{1}{3}\) (1)

Theo điều kiện có nghiệm của pt lượng giác bậc nhất:

\(m^2+\left(1-3m\right)\ge\left(m-2\right)^2\)

\(\Leftrightarrow1-3m\ge-4m+4\Rightarrow m\ge3\) (2)

Kết hợp (1); (2) \(\Rightarrow\) không tồn tại m thỏa mãn