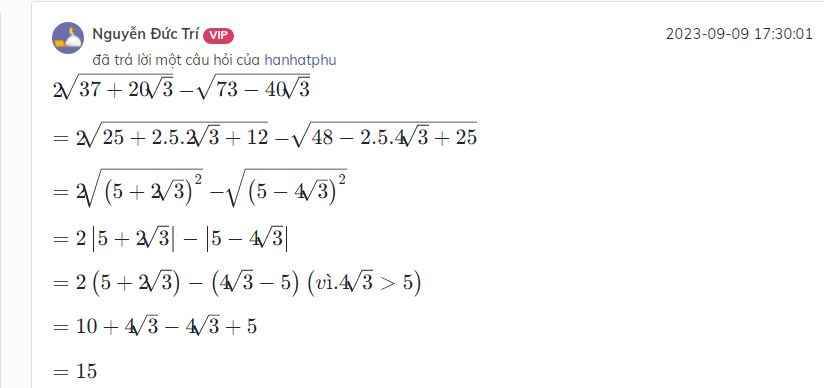\(2\sqrt[]{37+20\sqrt[]{3}}-\sqrt[]{73-40\sqrt[]{3}}\)

\(=2\sqrt[]{25+2.5.2\sqrt[]{3}+12}-\sqrt[]{48-2.5.4\sqrt[]{3}+25}\)

\(=2\sqrt[]{\left(5+2\sqrt[]{3}\right)^2}-\sqrt[]{\left(5-4\sqrt[]{3}\right)^2}\)

\(=2\left|5+2\sqrt[]{3}\right|-\left|5-4\sqrt[]{3}\right|\)

\(=2\left(5+2\sqrt[]{3}\right)-\left(4\sqrt[]{3}-5\right)\left(vì.4\sqrt[]{3}>5\right)\)

\(=10+4\sqrt[]{3}-4\sqrt[]{3}+5\)

\(=15\)

\(A=\dfrac{1}{2-\sqrt{3}}+\dfrac{1}{2+\sqrt{3}}-\sqrt{37-20\sqrt{3}}\)

\(=\dfrac{2+\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}+\dfrac{2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}-\sqrt{\left(5-2\sqrt{3}\right)^2}\)

\(=2+\sqrt{3}+2-\sqrt{3}-5+2\sqrt{3}\)

\(=2\sqrt{3}-1\)

= \(\sqrt{12-2.2\sqrt{3}.5+25}-\sqrt{12+2.2\sqrt{3}.5+25}\)

= \(\sqrt{\left(2\sqrt{3}-5\right)^2}-\sqrt{\left(2\sqrt{3}+5\right)^2}\)

= \(|2\sqrt{3}-5|-2\sqrt{3}-5\)

=\(5-2\sqrt{3}-2\sqrt{3}-5=-4\sqrt{3}\)

bây giờ vẫn còn công chúa

Trả lời:

\(\sqrt{37-20\sqrt{3}}-\sqrt{37+20\sqrt{3}}\)

\(=\sqrt{25-20\sqrt{3}+12}-\sqrt{25+20\sqrt{3}+12}\)

\(=\sqrt{\left(5-2\sqrt{3}\right)^2}-\sqrt{\left(5+2\sqrt{3}\right)^2}\)

\(=5-2\sqrt{3}-5-2\sqrt{3}\)

\(=-4\sqrt{3}\)

Bài 1 : 

Ta có : 

\(\sqrt{37-20\sqrt{3}}+\sqrt{37+20\sqrt{3}}=\sqrt{25-2.5.2\sqrt{3}+12}\)

\(+\sqrt{25+2.5.2\sqrt{3}+12}\)

\(=\sqrt{\left(5-2\sqrt{3}\right)^2}+\sqrt{\left(5+2\sqrt{3}\right)^2}\)

\(5-2\sqrt{3}+5+2\sqrt{3}\)

\(=5+5=10\)

Bài 2 : 

Với x , y , z > 0 . Ta có : 

+ ) \(\frac{x}{y}+\frac{y}{x}\ge2\left(1\right)\)

+ ) \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge\frac{9}{x+y+z}\left(2\right)\)

+ ) \(x^2+y^2+z^2\ge xy+yz+zx\Leftrightarrow\frac{x^2+y^2+z^2}{xy+yz+zx}\ge1\left(3\right)\)

Xảy ra đăng thức ở : \(\left(1\right),\left(2\right),\left(3\right)\Leftrightarrow x=y=z\) . Ta có : 

\(P=\frac{ab+bc+ca}{a^2+b^2+c^2}+\left(a+b+c\right)^2.\frac{\left(a+b+c\right)}{abc}\)

\(=\frac{ab+bc+ca}{a^2+b^2+c^2}+\left(a^2+b^2+c^2+2ab+2bc+2ca\right).\frac{\left(a+b+c\right)}{abc}\)

Áp dụng các bất đẳng thức (1) , (2) , (3) ta được : 

\(P\ge\frac{ab+bc+ca}{a^2+b^2+c^2}+\left(a^2+b^2+c^2\right).\frac{9}{ab+bc+ca}+2.9\)

\(=\left(\frac{ab+bc+ca}{a^2+b^2+c^2}+\frac{a^2+b^2+c^2}{ab+bc+ca}\right)+8.\frac{a^2+b^2+c^2}{ab+bc+ca}+18\)

\(\ge2+8+18=28\)

Dấu " = "  xảy ra \(\Leftrightarrow\hept{\begin{cases}a^2+b^2+c^2=ab+bc+ca\\ab=bc=ca\end{cases}\Leftrightarrow a=b=c}\)

a: \(=2\sqrt{20\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\cdot\sqrt{20\sqrt{3}}\)

\(=4\sqrt{5\sqrt{3}}-2\sqrt{5\sqrt{3}}-6\sqrt{5\sqrt{3}}=-4\sqrt{5\sqrt{3}}\)

b: \(=2\sqrt{5\sqrt{3}}-4\sqrt{2\sqrt{3}}-6\sqrt{5\sqrt{3}}=-4\sqrt{5\sqrt{3}}-4\sqrt{2\sqrt{3}}\)

a) Vì 20 °   <   70 °   n ê n   sin   20 °   <   sin 70 °  (góc tăng, sin tăng)

b) Vì 25 °   <   63 ° 15 '   n ê n   cos 25 °   >   cos   63 ° 15 ' (góc tăng, cos giảm)

c) Vì 73 ° 20 '   >   45 °   n ê n   t g 73 ° 20 '   >   t g 45 °  (góc tăng, tg tăng)

d) Vì 2 °   <   37 ° 40 '   n ê n   c o t g   2 °   >   c o t g   37 ° 40 '  (góc tăng, cotg giảm )