Cho hàm số y=-1/2x^2
a)Khảo sát và vẽ đồ thị (P) của hàm số trên
b)Lập phương trình đường thẵng ( d) đi qua A(-2;-2) và tiếp xúc với (P)
Cho hàm số \(y=\dfrac{1}{2}x^2\)
1) Khảo sát và vẽ đồ thị (P) của hàm số.
2) Cho A B, là hai điểm nằm trên đồ thị (P) lần lượt có hoành độ là -1 và +2.
a) Viết phương trình đường thẳng d đi qua A và có hệ số góc bằng \(\dfrac{1}{2}\)
b) Chứng tỏ điểm B cũng nằm trên đường thẳng d.
Cho hàm số \(y=\dfrac{1}{2}x^2\)
1) Khảo sát và vẽ đồ thị (P) của hàm số.
2) Cho A B, là hai điểm nằm trên đồ thị (P) lần lượt có hoành độ là -1 và +2.
a) Viết phương trình đường thẳng d đi qua A và có hệ số góc bằng \(\dfrac{1}{2}\)
b) Chứng tỏ điểm B cũng nằm trên đường thẳng d.
Cho hàm số y = x^4 + 2(m + 1)x^2 + 1
a) Khảo sát và vẽ đồ thị khi m = 1
b) Tìm m để đồ thị hàm số có 3 điểm cực trị. Tìm phương trình đường cong đi qua các điểm cực trị đó
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
a) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{x+2}\)
b) khảo sát và vẽ đồ thị hàm số \(y=\left|\dfrac{2x-3}{x+2}\right|\)
c) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{\left|x+2\right|}\)
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
Câu 1: Cho hàm số y=-125x\(^2\)
a) Khảo sát tính đơn điệu của hàm số
b) Tìm giá trị của m, n để các điểm A(1;m) và B (n; 125) thuộc đồ thị hàm số trên
Câu 2: Cho hàm số y=( m+1)x\(^2\)
a) Xác định m để đồ thị hàm số đi qua điểm A (1;2)
b) Vẽ đồ thị hàm số vừa tìm được
c) Tìm điểm thuộc parapol nói trên có hoành độ bằng -2
d) Tìm điểm thuộc parapol nói trên có tung độ bằng -8
d) Tìm điểm thuộc parapol nói trên có tung độ gấp ba lần hoành độ
Câu 2:
a) Để đồ thị hàm số \(y=\left(m+1\right)x^2\) đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào hàm số \(y=\left(m+1\right)x^2\), ta được:
m+1=2
hay m=1
Vậy: m=1
Cho hàm số y = 1/2 . x2 ( P)
a. Khảo sát và vẽ đồ thị (P) của hàm số trên
b. Cho A, B là hai điểm nằm trên đồ thị (P) lần lượt có hoành độ là -1 và 2
*Viết phương trình đường thẳng (d) qua A và có hệ số góc = 1/2
*Chứng tỏ điểm B cũng nằm trên đường thẳng (d)
a) (P) là parabol đi qua gốc toạ độ O(0; 0) ; điểm (1; 1/2) và điểm (-1;1/2)
b) A \(\in\) (P) => yA = \(\frac{1}{2}\). xA2 = \(\frac{1}{2}\). (-1)2 = \(\frac{1}{2}\)=> A (-1; \(\frac{1}{2}\))
B \(\in\) (P) => yB = \(\frac{1}{2}\).xB2 = \(\frac{1}{2}\).4 = 2 => B (2; 2)
+) đường thẳng có hệ số góc bằng \(\frac{1}{2}\) có dạng y = \(\frac{1}{2}\)x + b (d)
A \(\in\) d => yA = \(\frac{1}{2}\).xA + b => \(\frac{1}{2}\) = \(\frac{1}{2}\). (-1) + b => b = 1
Vậy đường thẳng (d) có dạng y = \(\frac{1}{2}\)x + 1
Nhận xét: yB = \(\frac{1}{2}\).xB + 1 => B \(\in\) (d)
Cho hàm số bậc nhất y=x+2 (d)
a) vẽ đồ thị hàm số trên
b) tìm tọa độ giao điểm của hàm số (d) với đồ thị của hàm số y=2x-1
b: Tọa độ giao điểm là:
2x-1=x+2 và y=x+2
=>3x=3 và y=x+2
=>x=1 và y=3
a: 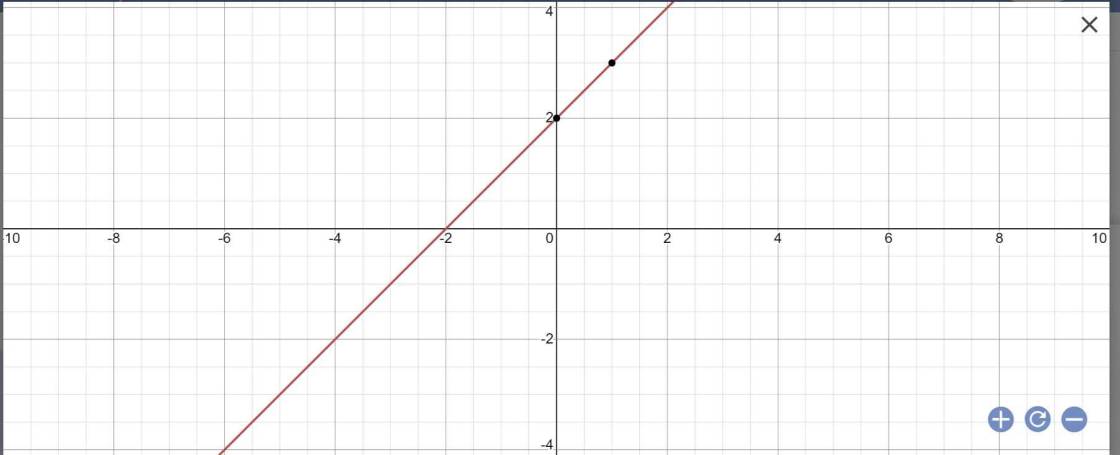
cho hàm số:
y=1/2x\(^2\)
1) Nêu tập xác định , chiều biến thiên và vẽ đồ thị của hàm số
2) Lập phương trình đướng thẳng đi qua điểm (2;-6)có hệ số góc a và tiếp xúc với đồ thị hàm số trên