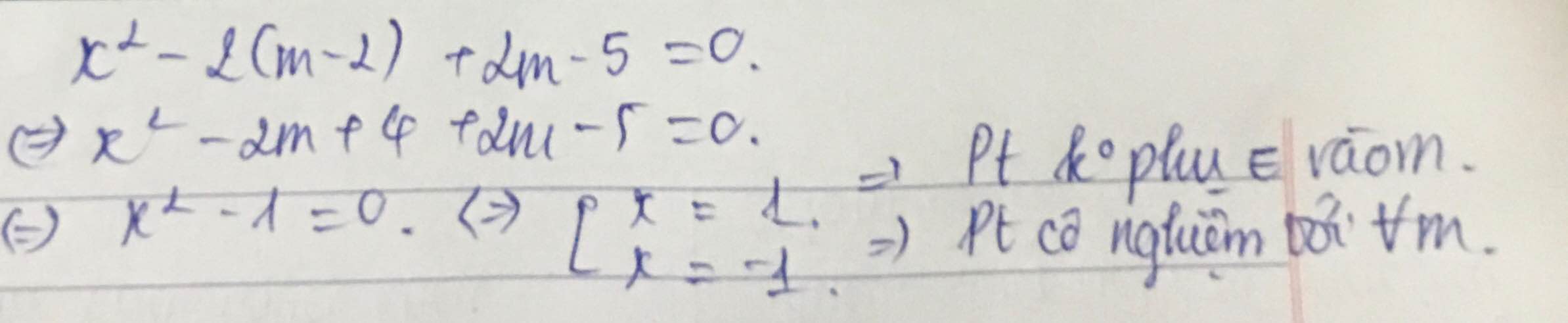ai đó giải hộ được không ạ  ' _ '

\(\Delta=\left(-m\right)^2-2.1.\left(m-1\right)\\ =m^2-2m+1\\ =\left(m-1\right)^2\)

Phương trình có hai nghiệm phân biệt :

\(\Leftrightarrow\Delta>0\\ \Rightarrow\left(m-1\right)^2>0\\ \Rightarrow m\ne1\)

Theo vi ét : 

\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)

\(x^2_1+x^2_2=x_1+x_2\\ \Leftrightarrow x^2_1+x^2_2=m\\ \Leftrightarrow\left(x^2_1+2x_1x_2+x_2^2\right)-2x_1x_2=m\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-m=0\\ \Leftrightarrow m^2-2\left(m-1\right)-m=0\\ \Leftrightarrow m^2-2m+2-m=0\\ \Leftrightarrow m^2-3m+2=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(loại\right)\\m=2\left(t/m\right)\end{matrix}\right.\)

Vậy \(m=2\)

\(\Delta=\left(2m+4\right)^2-4\left(3m+2\right)\)

\(=4m^2+16m+16-12m-8\)

\(=4m^2+4m+8\)

\(=\left(2m+1\right)^2+7>0\)

Do đó: Phương trình luôn có hai nghiệm phân biệt

Theo Vi-et, ta được:

\(\left\{{}\begin{matrix}x_1+x_2=2m+4\\x_1x_2=3m+2\end{matrix}\right.\)

Theo đề, ta có hệ phương trình:

\(\left\{{}\begin{matrix}x_1+x_2=2m+4\\-2x_1+x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_1=2m+1\\x_1+x_2=2m+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{2}{3}m+\dfrac{1}{3}\\x_2=2m+4-\dfrac{2}{3}m-\dfrac{1}{3}=\dfrac{4}{3}m+\dfrac{11}{3}\end{matrix}\right.\)

Ta có: \(x_1x_2=3m+2\)

nên \(\left(\dfrac{2}{3}m+\dfrac{1}{3}\right)\left(\dfrac{4}{3}m+\dfrac{11}{3}\right)=3m+2\)

\(\Leftrightarrow m^2\cdot\dfrac{8}{9}+\dfrac{22}{9}m+\dfrac{4}{9}m+\dfrac{11}{9}=3m+2\)

\(\Leftrightarrow m^2\cdot\dfrac{8}{9}-\dfrac{1}{9}m-\dfrac{7}{9}=0\)

\(\Leftrightarrow8m^2-m-7=0\)

\(\Leftrightarrow\left(m-1\right)\left(8m+7\right)=0\)

=>m=1 hoặc m=-7/8

a: Khi m=1 thì (1): x^2-2(1-2)x+1^2-5-4=0

=>x^2+2x-8=0

=>(x+4)(x-2)=0

=>x=2 hoặc x=-4

b: Δ=(2m-4)^2-4(m^2-5m-4)

=4m^2-16m+16-4m^2+20m+16

=4m+32

Để pt có hai nghiệm phân biệt thì 4m+32>0

=>m>-8

x1^2+x2^2=-3x1x2-4

=>(x1+x2)^2+x1x2+4=0

=>(2m-4)^2+m^2-5m-4+4=0

=>4m^2-16m+16+m^2-5m=0

=>5m^2-21m+16=0

=>(m-1)(5m-16)=0

=>m=16/5 hoặc m=1

Làm câu b)

Để phương trình có hai nghiệm phân biệt:

\(\Delta'\ge0\Leftrightarrow3^2-\left(m+1\right)\ge0\Leftrightarrow m\le8\)

Áp dụng định lí Vi-ét ta có:

\(\hept{\begin{cases}x_1+x_2=6\\x_1.x_2=m+1\end{cases}}\)(1)

Xét: \(x^2_1+x^2_2=3\left(x_1+x_2\right)\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=3\left(x_1+x_2\right)\)(2)

Từ 1, 2 ta có:

\(6^2-2\left(m+1\right)=3.6\Leftrightarrow m=8\)(tm)

Vậy ...

a) Với m= 2, ta có phương trình:  x 2 + 2 x − 3 = 0

Ta có:  a + b + c = 1 + 2 − 3 = 0                                                             

Theo định lý Viet, phương trình có 2 nghiệm: 

x 1 = 1 ;   x 2 = − 3 ⇒ S = 1 ;   − 3 .                                                                             

b) Chứng minh rằng phương trình luôn có nghiệm  ∀ m .

Ta có:  Δ ' = m − 1 2 − 1 + 2 m = m 2 ≥ 0 ;    ∀ m                                           

Vậy phương trình luôn có nghiệm  ∀ m .                                              

c) Theo định lý Viet, ta có: x 1 + x 2 = − 2 m + 2 x 1 . x 2 = 1 − 2 m                                                             

Ta có:

x 1 2 . x 2 + x 1 . x 2 2 = 2 x 1 . x 2 + 3 ⇔ x 1 . x 2 x 1 + x 2 − 2 = 6 ⇒ 1 − 2 m − 2 m + 2 − 2 = 6 ⇔ 2 m 2 − m − 3 = 0                  

Ta có: a − b + c = 2 + 1 − 3 = 0 ⇒ m 1 = − 1 ;   m 2 = 3 2                                                  

Vậy m= -1 hoặc m= 3/2