Cho tam giác ABC vuông tại A có AB=12cm; AC=16cm. Kẻ đường cao AH a) Chứng minh /\HBA~/\ABC b) Tính diện tích /\HBA bt tỉ số đồng dạng của/\ABC và /\HBA là 5/3

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB = 12cm, BC = 15cm. Diện tích tam giác ABC là :
\(S=\dfrac{12\cdot9}{2}=6\cdot9=54\left(cm^2\right)\)
Đúng 0
Bình luận (0)
bổ sung
A. 108cm2 B. 54cm C. 54cm2 D. 15cm2
Đúng 0
Bình luận (0)
a/ Cho tam giác ABC vuông tại B có AB=12cm,BC=16cm.Tính AC
b/ Cho tam giác DBC vuông tại C có CB=3cm,BD=5cm.Tính CD
Áp dụng định lí Pytago ta có
\(a,BC^2=AB^2+BC^2=12^2+16^2\\ =\sqrt{400}=20\\ b,BD^2=BC^2+CD^2\\ 5^2=3^2+CD^2\\ CD^2=5^2-3^2=\sqrt{16}=4\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có AB16cm,AC12cm. Kẻ AH vuông góc với BC tại H . Gọi S tam ABC là diện tích tam giác ABC 1) tính diện tích tam giác abc 2) tính BC,AH 3)tính BH,CH giúp...
Đọc tiếp
cho tam giác ABC vuông tại A có AB=16cm,AC=12cm. Kẻ AH vuông góc với BC tại H . Gọi S tam ABC là diện tích tam giác ABC 1) tính diện tích tam giác abc 2) tính BC,AH 3)tính BH,CH giúp mình vs ạ
1) Có \(\Delta ABC\) vuông
=> S\(\Delta ABC\) = \(\dfrac{AB.AC}{2}\) = \(\dfrac{16.12}{2}\) = 96 (cm2)
2) Có \(\Delta ABC\) vuông , theo định lý Pytago ta có :
AB2 + AC2 = BC2
=> 162 + 122 = BC2
=> 400 = BC2
=> BC = 20 (cm)
Ta có : S\(\Delta ABC\) = S\(\Delta ABH\) + S\(\Delta ACH\)
=> \(\dfrac{BH.AH}{2}+\dfrac{HC.AH}{2}=S\Delta ABC\)
=> \(\dfrac{BH.AH+HC.AH}{2}=S\Delta ABC\)
=> \(\dfrac{AH.\left(BH+HC\right)}{2}=S\Delta ABC\)
=> \(\dfrac{AH.BC}{2}\) = 96
=> AH = 96 . \(\dfrac{2}{BC}\) = 96 . \(\dfrac{2}{20}\) = 9.6 (cm)
3) Có \(\Delta ABH\) vuông , theo định lý Pytago ta có :
BH2 = AB2 - AH2
=>BH2 = 162 - 9.62 = 163.84
=> BH = 12.8 (cm)
=> CH = BC - BH = 20 - 12.8 = 7.2 (cm)
Đúng 2
Bình luận (0)
Bài 1: Cho tam giác MNP vuông tại N có MN=6cm, MP=10cm. Tính độ dài NP.
Bài 2; Cho tam giác ABC vuông tại A. Tính cạnh BC trong các TH sau:
a. AB=8cm; AC=6cm
b, AB=12cm; AC=16cm
c. AB=5cm; AC=12cm.
Bài 2:
a: \(BC=\sqrt{8^2+6^2}=10\left(cm\right)\)
b: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
c: \(BC=\sqrt{5^2+12^2}=13\left(cm\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC có BC = 12cm , AC = 5cm , AB = 13cm . Chọn khẳng định đúng
A . tam giác ABC là tam giác vuông tại A
B. tám giác ABC là tam giác nhọn
C. tam giác ABC là tam giác vuông tại C
D . tam giác ABC là tam giác tù
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, AB= 12cm, BC= 20cm. Giải tam giác ABC
Áp dụng định lý Py-ta-go vào tam giác vuông ABC ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}\)
\(\Rightarrow AC=\sqrt{20^2-12^2}=16\left(cm\right)\)
Mà: \(sinB=\dfrac{AC}{BC}=\dfrac{16}{20}\)
\(\Rightarrow sinB=\dfrac{4}{5}\Rightarrow\widehat{B}\approx53^o\)
\(\Rightarrow\widehat{C}=180^o-90^o-53^o\approx37^o\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB<AC) có đường cao AH, biết AB=12cm, AC=16cm
a) Tính BC và AH
b) Chứng minh tam giác BHA đồng dạng tam giác ABC
a: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
AH=12*16/20=192/20=9,6cm
b: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
góc B chung
=>ΔBHA đồng dạng với ΔBAC
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A có BC 15cm, AB 12cm. Tính AC,
B
^
A. AC 8 (cm);
B
^
≈
36
0
52
B. AC 9 (cm);
B
^
≈
36
0
52
C. AC 9 (cm);
B
^
≈
37...
Đọc tiếp
Cho tam giác ABC vuông tại A có BC = 15cm, AB = 12cm. Tính AC, B ^
A. AC = 8 (cm); B ^ ≈ 36 0 52 '
B. AC = 9 (cm); B ^ ≈ 36 0 52 '
C. AC = 9 (cm); B ^ ≈ 37 0 52 '
D. AC = 9 (cm); B ^ ≈ 36 0 55 '
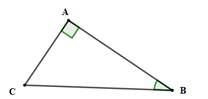
Xét tam giác ABC vuông tại A có:
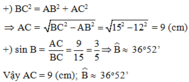
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có AB=12cm,Ac=16cm kẻ đường cao AH(h thuộc BC) tính diện tích tam giác ABC
Do tam gaics ABC vuông tại A nên:
\(S_{ABC}=\dfrac{1}{2}AB.AC=96\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có: BC 20cm; AC 12cm. Quay tam giác ABC cạnh AB ta được một hình nón có thể tích là: A. 2304
π
(
c
m
3
) B. 1024
π
(
c
m
3
) C. 786
π
(
c
m
3
) D. 768
π
(
c
m
3
)
Đọc tiếp
Cho tam giác ABC vuông tại A có: BC = 20cm; AC = 12cm. Quay tam giác ABC cạnh AB ta được một hình nón có thể tích là:
A. 2304 π ( c m 3 )
B. 1024 π ( c m 3 )
C. 786 π ( c m 3 )
D. 768 π ( c m 3 )


























