Cho hàm số y = (m + 1)sinx + mcosx - (m+2)x + 1. Tìm giá trị của m để y' = 0 có nghiệm
Cho hàm số y = (m + 1)sinx + mcosx – (m + 2)x + 1. Tìm giá trị của m để y’ = 0 có nghiệm?
A. 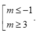
B. m ≥ 2.
C. -1 ≤ m ≤ 3.
D. m ≤ -2.
Chọn A.
y' = (m + 1)cosx – msinx – ( m + 2)
Phương trình y’ = 0 ⇔ (m + 1)cosx – msinx = (m + 2)
Điều kiện phương trình có nghiệm là a2 + b2 ≥ c2
⇔ (m + 1)2 + m2 ≥ (m + 2)2 ⇔ m2 – 2m – 3 ≥ 0 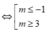
Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số y = 4x + (m+1)sinx+ mcosx đồng biến trên ℝ Số phần tử của S là.
A. 4.
B. 6.
C. 5.
D. Vô số.
cho hàm số y=(x-1)/(x+1) (C)
1,Khảo sát sự biến thiên và vẽ đồ thị hàm số
2,Tìm m để phương trình có nghiệm thuộc (0;π) : ((sinx-1)/(sinx+1))=m
Cho hàm số y = ( m - 1 ) sin x - 2 sin x - m . Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng ( 0 ; π 2 ) .
A.![]() .
.
B.![]() .
.
C.![]() .
.
D.![]() .
.
Chọn A
Điều kiện: ![]() . Điều kiện cần để hàm số
. Điều kiện cần để hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() là
là![]() .
.
Ta có : 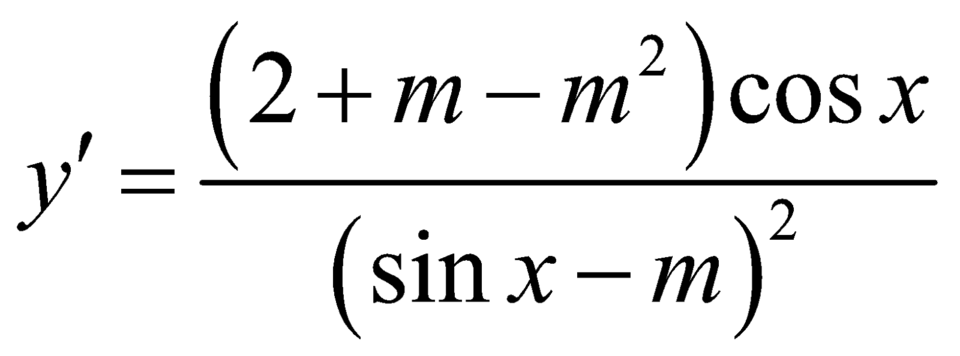 .
.
Ta thấy ![]()
![]() .
.
Để ham số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() là
là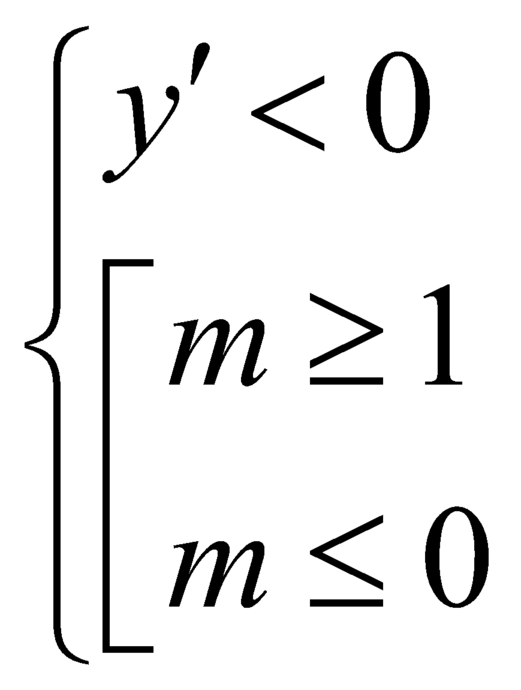
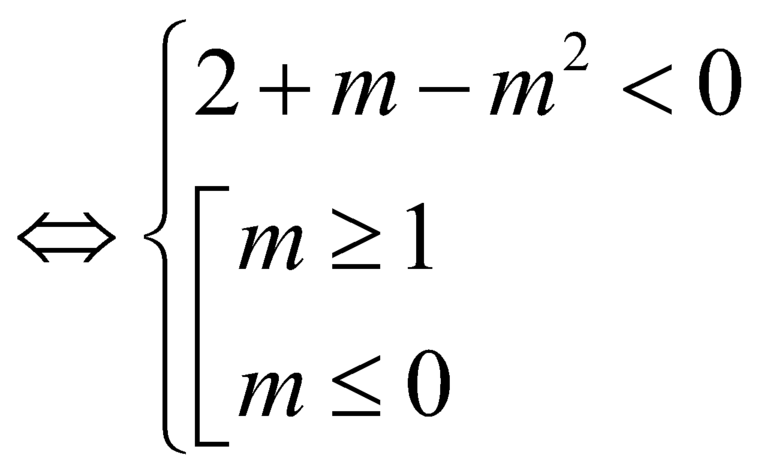
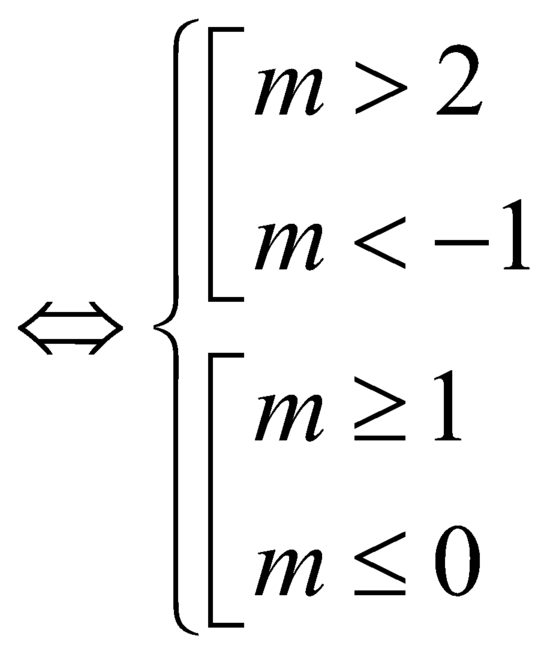
![]() .
.
Cho hàm số y = 2 cos 3 x - 3 cos 2 x - m cos x . Tìm tất cả các giá trị của m để hàm số đã cho nghịch biến trên khoảng 0 ; π 2
A. m ∈ [ - 3 2 ; + ∞ )
B. m ∈ - 2 ; 3 2
C. m ∈ 3 2 ; 2
D. m ∈ ( - ∞ ; - 3 2 ]
Cho hàm số y = 2 cos 3 x - 3 cos 2 x - m cos x . Tìm tất cả các giá trị của m để hàm số đã cho nghịch biến trên khoảng 0 ; π 2
A. m ∈ [ - 3 2 ; + ∞ )
B. m ∈ - 2 ; 3 2
C. m ∈ 3 2 ; 2
D. m ∈ ( - ∞ ; - 3 2 ]
Chọn D.
Cách 1:
![]()
![]()
Hàm số y = 2 cos 3 x - 3 cos 2 x - m cos x nghịch biến trên khoảng 0 ; π 2
![]()

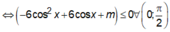
![]()
Xét 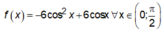
Đặt t = cosx
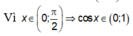
Ta có: ![]() là Parabol có đỉnh
là Parabol có đỉnh 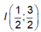 và hệ số a < 0 nên có giá trị lớn nhất là
3
2
tại t =
1
2
và hệ số a < 0 nên có giá trị lớn nhất là
3
2
tại t =
1
2
Để (1) xảy ra 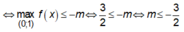
Cách 2:
Đặt t = cosx
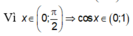
Ta có:
![]()
Hàm số y =
2
cos
3
x
-
3
cos
2
x
-
m
cos
x
nghịch biến trên khoảng
0
;
π
2
thì ![]() đồng biến trên khoảng (0;1)
đồng biến trên khoảng (0;1)
![]()
![]()
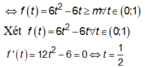
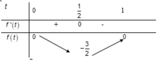
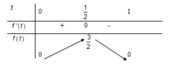
Dựa vào bảng biến thiên suy ra ![]()
Tìm các giá trị của tham số m để hàm số y=m sinx+7x-5m+3 có y' ≥ 0,với mọi x thuộc R
A.![]()
B. ![]()
C. ![]()
D. ![]()
1. Tìm tất cả các giá trị thực của tham số m để hàm số y= mx - sin3x đồng biến trên khoảng ( trừ vô cùng ; cộng vô cùng) 2. Tìm tất cả các giá trị thực của tham số m để hàm số y = x + mcosx đồng biến trên khoảng( trừ vô cùng ; cộng vô cùng)
1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)
1. Chứng minh phương trình x4 + (m2-m)x3 +mx2 - 2mx -2 = 0 luôn có nghiệm thuộc khoảng (0;2) với mọi giá trị của tham số m.
2. Cho hàm số y = \(\dfrac{x+1}{x-1}\) có đồ thị (C). Tìm tất cả giá trị của tham số m để đường thẳng (d): y = 2x + m cắt (C) tại hai điểm phân biệt mà hai tiếp tuyến của (C) tại hai điểm đó song song với nhau.
3. Chứng minh rằng với mọi giá trị của tham số m thì phương trình \(x^4+mx^3-4x^2-mx+1=0\) luôn có nghiệm trên khoảng (0;1).
4. Cho hàm số: y = \(\dfrac{1}{3}x^3-\left(m+1\right)x^2+\left(2m+4\right)x-3\) có đồ thị (Cm) (với m là tham số). Tìm m để trên đồ thị (Cm) có hai điểm phân biệt có hoành độ cùng dấu và tiếp tuyến của (Cm) tại mỗi điểm đó vuông góc với đường thẳng d: \(x+3y-6=0\)
5. Cho hàm số y = \(\dfrac{x+1}{x-2}\) có đồ thị (C); đường tròn (T) có tâm I(2;-5) và đi qua điểm E(3;-1). Tìm toạ độ các điểm M thuộc đồ thị (C) để tiếp tuyến của (C) tại M cắt đường tròn (T) tại hai điểm A, B sao cho tam giác EAB vuông tại E.
Toi mới làm được câu 2 thoi à :( Mấy câu còn lại để rảnh nghĩ thử coi sao
\(PTHDGD:\dfrac{x+1}{x-1}=2x+m\Leftrightarrow x+1=\left(2x+m\right)\left(x-1\right)\)
\(\Leftrightarrow x+1=2x^2-2x+mx-m\Leftrightarrow2x^2+\left(m-3\right)x-m-1=0\)
De ton tai 2 diem phan biet \(\Leftrightarrow\Delta>0\Leftrightarrow\left(m-3\right)^2+8m+8>0\Leftrightarrow m^2+2m+17>0\Leftrightarrow\left(m+1\right)^2+16>0\forall x\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=\dfrac{3-m}{2}\\x_1x_2=\dfrac{-m-1}{2}\end{matrix}\right.\)
Vi 2 tiep tuyen tai 2 diem x1, x2 song song voi nhau
\(\Rightarrow f'\left(x_1\right)=f'\left(x_2\right)\)
\(f'\left(x\right)=\dfrac{x-1-x-1}{\left(x-1\right)^2}=-\dfrac{2}{\left(x-1\right)^2}\)
\(\Rightarrow\dfrac{1}{\left(x_1-1\right)^2}=\dfrac{1}{\left(x_2-1\right)^2}\Leftrightarrow x_1^2-2x_1+1=x_2^2-2x_2+1\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)-2\left(x_1-x_2\right)=0\Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=x_2\left(loai\right)\\x_1+x_2=2\end{matrix}\right.\Leftrightarrow\dfrac{3-m}{2}=2\Leftrightarrow m=-1\)