Cho hình bình hành ABCD
AB=8cm, AD= 6cm
AM cắt BD tại I, cắt CD tại N
a) Tính \(\dfrac{IB}{ID}\)
b) Chứng minh tam giác MAB đồng dạng tam giác AND
c) Tính DN và CN
d) Chứng minh IA2=IM.IN
Những câu hỏi liên quan
Cho hình bình hành ABCD có AB = 8cm, AD = 6cm. Trên cạnh BC lấy M sao cho BM = 4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng DC tại N.a) Tính tỉ số IB/IDb) Chứng minh ΔMAB và ΔAND đồng dạngc) Tính độ dài DN và CNd) Chứng minh IA2 = IM.IN
đây là toán lớp 8 mà
Cho hình bình hành ABCD có
A
B
8
c
m
,
A
D
6
c
m
.
Trên cạnh BC lấy M sao cho BM 4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng DC tại N.a) Tính tỉ số IB/IDb) Chứng minh ΔMAB và ΔAND đồng dạngc) Tính độ dài DN và CNd) Chứng minh
I
A
2
...
Đọc tiếp
Cho hình bình hành ABCD có A B = 8 c m , A D = 6 c m . Trên cạnh BC lấy M sao cho BM = 4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng DC tại N.
a) Tính tỉ số IB/ID
b) Chứng minh ΔMAB và ΔAND đồng dạng
c) Tính độ dài DN và CN
d) Chứng minh I A 2 = I M . I N
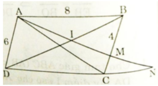
a) AD // BC (gt)
b) Xét ΔAMB và ΔNAD có:
∠BAM = ∠ AND (so le trong, AB // CD)
∠ABM = ∠ADN (góc đối của hình bình hành)
⇒ ΔAMB ∼ ΔNAD (g.g)
c) ΔAMB ∼ ΔNAD (cmt)
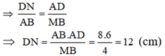
Do đó: CN = DN – DC = 12 – 8 = 4 (cm)
d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có
Tương tự, do AD // BM nên
Đúng 0
Bình luận (0)
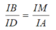
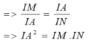
cho honhf bình hành abcd có ab=8cm, ad=6cm, trên cạnh bc lấy điểm m sao cho bm=4cm. đường thẳng am cắt đường chéo bd tại i cắt đường thẳng dc tại n
tính tỉ số ib/id, chứng minh tam giác mab, tam giác and đồng dạng ; tính độ dài dn và cn; chứng minh ia=im*in
Cho hình bình hành ABCD có AB=8cm, AD=6cm. Trên cạnh BC lấy M sao cho BM= 4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng DC tại N.
a) Chứng minh tam giác MAB đồng dạng tam giác AND
b) Tính độ dài DN và CN
Cho hình bình hành ABCD có AB= 8cm ,AD=6cm. Trên cạnh BC lấy điểm M sao cho BM=4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng BC tại N.
a. tính tỉ số IB = ID
b. CM: Tam giác AMB đồng dạng tam giác AND. Tính độ dài DN và CN
c. CM . IA^2 = IM.IN
cho hình bình hànhABCD có AD=6cm,AB=8cm . Trên cạnh BC lấy M sao cho BM=2/3BC. Đường thẳng AM cắt đường chéo BD tại I và cắt đường thẳng DC tại N
a) Chứng minh tam giác MAB đồng dạng tam giác AND
Từ (1) // CD AB // ND
(5)
Từ (1) (2 góc đối của hình bình hành) (6)
Từ (5), (6) (G-G)
Đúng 1
Bình luận (0)
cho hình bình hành ABCD có AB=8cm,AD=6cm.Trên cạnh BC lấy M sao cho BM=4cm.Đường thẳng AM cắt đường chéo BD tại I và cắt đường thẳng DC tại N.
a.Tính tỉ số IBIDIBID?
b.C/m tam giác AMB và tam giác AND đồng dạng.
Tính DN,CN?
c.C/m IA2=IM.IN
Cho hình bình hành ABCD có BA=8cm,AD=6cm,trên cạnh BC lấy điểm M sao cho BM=4cm.đường thẳng AM cắt BD tại i,AM cắt đường thẳng DC tại N.
a,tính tỉ số IB/ID
b,Tính DN,CN
c,Chứng minh AI2=IM.IN
Bài 1: Cho hình vuông ABCD và hai đường chéo AC và BD cắt nhau tại O. Lây điểm N thuộc đoạn AC sao cho AN = ½ NC. DN cắt AB tại I. a) Chứng minh: tam giác ANI đồng dạng với tam giác CND b) Chứng minh: OI// AD c) Gọi E là trung điểm của đoạn OA, đường thắng DE cắt AB tại F. Chứng minh AFN = AEI d) Chứng minh: DE. DF = DN. DI
a) Xét ΔANI và ΔCND có
\(\widehat{ANI}=\widehat{CND}\)(hai góc đối đỉnh)
\(\widehat{IAN}=\widehat{DCN}\left(=45^0\right)\)
Do đó: ΔANI\(\sim\)ΔCND(g-g)
Đúng 0
Bình luận (0)