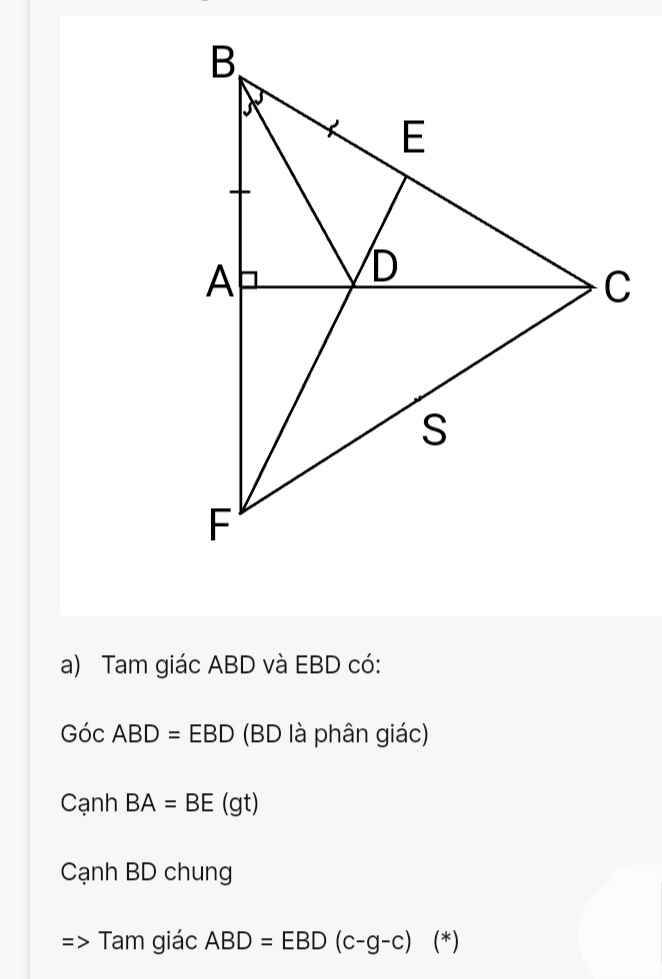
Cho tam giác ABC vuông tại A.Phân giác của góc B cắt AC tại D.Kẻ DE vuông góc BC tại E,DE cắt AB tại F a,Chứng minh tam giác ABD=tam giác EBD b, chứng minh BF=BC và BD vuông góc CF

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có BC=10cm;AB=6cm
a)Tính độ dài AC
b)Tia phân giác của góc ABC cắt AC tại D.Kẻ DE vuông góc BC tại E
Chứng minh tam giác ABD= tam giác EBD
c) Gọi F lafd giao điểm của hai đường thẳng AB và DE
So sánh DE với DF và chứng minh BD vuông góc CF
a, tam giác ABC vuông tại A (gt)
=> AB^2 + AC^2 = BC^2 (đl Pytago)
có AB = 6; BC = 10
=> AC = 8 do AC > 0
b, xét tam giác DAB và tam giác DEB có : BD chung
^DAB = ^DEB = 90
^ABD = ^EBD do BD là phân giác của ^ABC (gt)
=> tg DAB = tg DEB (ch-gn)
c, tg DAB = tg DEB (câu b)
=> DA = DE (Đn)
xét tg DAF và tg DEC có : ^DAF = ^DEC = 90
^ADF = ^EDC (Đối đỉnh)
=> tg DAF = tg DEC (cgv-gnk)
=> DF = DC (đn)
có DC > DE
=> DE < DF
+ xét tg CFB có : CA _|_ FB; FE _|_ BC mà FE cắt CA tại D
=> BD _|_ CF
Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc ABC cắt AC tại D. Từ D kẻ DE vuông góc với BC tại E.
a) Chứng minh tam giác ABD bằng tam giác EBD .
b) Gọi F là giao điểm của AB và DE. Chứng minh BF = BC.
c) Kẻ đường cao AH của AFC . Chứng minh AE vuông góc với AH
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc FBE chung
=>ΔBEF=ΔBAC
=>BF=BC
c: ΔBFC cân tại B
mà BD là phân giác
nên BD vuông góc CF
=>BD//AH
=>AH vuông góc AE
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A,có B=600 và AB=5cm.Tia phân giác của góc B cắt AC tại D.Kẻ DE vuông góc với BC tại E.
a)Chứng minh:△ABD=△EBD và BA=BE.
b)Chứng minh:△ABE là tam giác đều.
c)Tính độ dài cạnh BC.
`a)`
+, `Delta ABC` vuông tại `A(GT)=>hat(A)=90^0`
`DE⊥BC(GT)=>hat(BED)=90^0`
`BD` là p/g của `hat(ABC)(GT)=>hat(B_1)=hat(B_2)`
Xét `Delta ABD` và `Delta EBD` có :
`{:(hat(A)=hat(BED)(=90^0)),(BD-chung),(hat(B_1)=hat(B_2)(cmt)):}}`
`=>Delta ABD=Delta EBD(c.h-g.n)(đpcm)`
+, Có `Delta ABD=Delta EBD(cmt)`
`=>BA=BE` ( 2 cạnh t/ứng ) `(đpcm)`
`b)`
Có `BA=BE(cmt)`
`=>Delta ABE` cân tại `B`
mà `hat(ABE)=60^0(hat(ABC)=60^0)`
nên `Delta ABC` đều `(đpcm)`
`c)`
Có `Delta ABC` vuông tại `A=>hat(ABC)+hat(C)=90^0`
hay `60^0+hat(C)=90^0`
`=>hat(C)=90^0-60^0=30^0` (1)
`Delta ABE` đều `(cmt)=>hat(A_1)=60^0`
`=>hat(A_2)=30^0` (2)
Từ `(1)` và `(2)=>Delta EAC` cân tại `E`
`=>AE=EC`
Có `Delta ABE` đều `(cmt)=>AB=AE`
mà `AE=EC(cmt)`
`{:(nên EC=AB),(mà AB=EB(cmt);AB=5cm):}}`
`=>EC=EB=5cm`
Vậy `BC=EC+EB=5+5=10(cm)`
Đúng 2
Bình luận (0)
a: Xet ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE
b: BA=BE và góc ABE=60 độ
=>ΔBAE đều
c: Xét ΔABC vuông tại A có cos B=AB/BC
=>5/BC=1/2
=>CB=10cm
Đúng 3
Bình luận (0)
cho tam giác ABC vuông tại A tia phân giác góc ABC cat AC tại D vẽ DE vuông góc với BC(E thuộc BC) AE cắt BD tại F đường thẳng vuông góc với BC tại B cắt CA tại M gọi I là giao điểm bất kỳ thuộc đường thẳng AB trên tia đối AB lấy J sao cho AJBIa) chứng minh tam giác ABD tam giác EBD và AD DEb) chứng minh ADDC c) chứng minh CF là trung tuyến của tam giác ACEd) chứng minh RJ vuông góc JC
Đọc tiếp
cho tam giác ABC vuông tại A tia phân giác góc ABC cat AC tại D vẽ DE vuông góc với BC(E thuộc BC) AE cắt BD tại F đường thẳng vuông góc với BC tại B cắt CA tại M gọi I là giao điểm bất kỳ thuộc đường thẳng AB trên tia đối AB lấy J sao cho AJ=BI
a) chứng minh tam giác ABD = tam giác EBD và AD = DE
b) chứng minh AD<DC
c) chứng minh CF là trung tuyến của tam giác ACE
d) chứng minh RJ vuông góc JC
Xin lỗi mk ko biết vẽ hình trên máy
a) Xét tam giác ABD và tan giác EBD có :
BD chung
góc ABD = góc EBD ( vì BD la phân giác góc B )
góc A = góc E ( = 90 )
=> Tam giác ABD = tam giác EBD ( cạnh huyền- góc nhọn )
=> AD = DE
Chúc bạn hc tốt
Đúng 1
Bình luận (1)
Cho tam giác vuông ABC vuông tại A có AB < AC. Tia phân giác của góc ABC cắt AC tại D. Qua D kẻ DE vuông góc với BC.
a. Chứng minh tam giác ABD bằng tam giác EBD.
b. Tia ED cắt tia BA tại F. Chứng minh BF = BC.
c. Chứng minh AE // CF.
d. Chứng minh DC^2 - DA^2 = (BC - BA)^2
Câu 4: Cho tam giác ABC vuông tại A(AB < AC) phân giác góc B cắt AC tại D .Kẻ DE vuông góc BC tại E. a/Chứng minh tam giác ABD = tam giác EBD b/Chứng minh BD là đường trung trực của đoạn thẳng AB. c/ Chứng minh: AB + AC > BC + DF
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=goc EBD
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>BA=BE; DA=DE
=>BD là trung trực của AE
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AB= 3cm, AC= 4cm. Phân giác của góc B cắt AC tại D. Kẻ DE vuông góc BC tại E a. Tính BC b. Chứng minh tam giác ABD= tam giác EBD c. So sánh BD với BC+CD từ đó chứng minh BD+DA < BC+AC
Cho tam giác ABC vuông tại A (AB<AC), kẻ BD là phân giác của góc ABC (D thuộc AC). Vẽ DE vuông góc với BC tại E. a) Chứng minh tam giác ABD = tam giác EBD. b) AE cắt BD tại I. Chứng minh BD vuông góc với AE và I là trung điểm AE. c) Cẽ tia Cx vuông góc với tia BD tại H. Trên tia đối của tia AB lấy điểm F sao cho AF = EC. Chứng minh 3 điểm C,H,F thẳng hàng và AE // FC.
a) Ta có:
- Góc ABD là góc giữa hai phân giác của góc ABC, nên ABD = CBD.
- Góc EBD là góc giữa phân giác của góc ABC và đường thẳng DE, nên EBD = CBD.
Vậy tam giác ABD = tam giác EBD.
b) Ta có:
- Góc ABD = góc EBD (do chứng minh ở câu a).
- Góc ADB = góc EDB (do cùng là góc vuông).
- Vậy tam giác ABD = tam giác EBD (do hai góc bằng nhau và góc giữa hai cạnh bằng nhau).
- Do đó, BD vuông góc với AE.
- Ta có AE cắt BD tại I, vậy I là trung điểm của AE.
c) Ta có:
- Tia Cx vuông góc với tia BD tại H.
- Trên tia đối của tia AB, lấy điểm F sao cho AF = EC.
- Ta cần chứng minh 3 điểm C, H, F thẳng hàng và AE // FC.
- Vì AF = EC và tam giác ABD = tam giác EBD (do chứng minh ở câu a), nên tam giác AFB = tam giác EFC (do hai cạnh bằng nhau và góc giữa hai cạnh bằng nhau).
- Vậy 3 điểm C, H, F thẳng hàng và AE // FC.
Đúng 1
Bình luận (0)
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>BA=BE và DA=DE
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD vuông góc với AE tại trung điểm I của AE
c: Xét ΔBFC có \(\dfrac{BA}{AF}=\dfrac{BE}{EC}\)
nên AE//CF
Ta có: BD\(\perp\)AE
AE//CF
Do đó: BD\(\perp\)CF
mà BD\(\perp\)CH
và CH,CF có điểm chung là C
nên C,H,F thẳng hàng
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, biết AC =12cm, BC=13cm
a) Tính AB
b) Tia phân giác BD cắt AC tại D, trên tia BC lấy điểm E sao ch BE=BA. Chứng minh tam giác ABD= tam giác EBD
c) Chứng minh DE vuông góc BC
d) DE cắt AB tại F. Chứng minh AF=EC
xl mình ko làm đc
`Answer:`

a. Vì `\triangleABC` vuông tại `A` nên theo định lí Pytago, ta có:
\(AB^2=BC^2-AC^2\Leftrightarrow AB^2=13^2-12^2\Leftrightarrow AC^2=169-144=25\Leftrightarrow AC=5cm\)
b. Xét `\triangleABD` và `\triangleEBD:`
`BD` chung
`BA=BE`
`\hat{ABD}=\hat{EBD}`
`=>\triangleABD=\triangleEBD(c.g.c)`
c. Theo phần b. `\triangleABD=\triangleEBD`
`=>\hat{BAD}=\hat{BED}=90^o`
`=>DE⊥BC`
d. Xét `\triangleADF` và `triangleEDC:`
`AD=DE`
`\hat{DAF}=\hat{DEC}=90^o`
`\hat{ADF}=\hat{EDC}`
`=>\triangleADF=\triangleEDC(g.c.g)`
`=>AF=BC`