Xét vị trí tương đối của mp x-2y-2z+1=0 và mặt cầu x^2+y^2 -2x+4y+8z-4=0

Những câu hỏi liên quan
Vị trí tương đối của hai mặt cầu:
x
2
+
y
2
+
z
2
+ 2x - 2y - 2z - 7 0 và
x
2
+
y
2
+
z
2
+ 2x + 2y + 4z + 5 0 là: A. ở ngoài nhau B. tiếp xúc C. cắt nhau D....
Đọc tiếp
Vị trí tương đối của hai mặt cầu: x 2 + y 2 + z 2 + 2x - 2y - 2z - 7 = 0 và x 2 + y 2 + z 2 + 2x + 2y + 4z + 5 = 0 là:
A. ở ngoài nhau
B. tiếp xúc
C. cắt nhau
D. chứa nhau
Đáp án C
Mặt cầu: x 2 + y 2 + z 2 + 2x - 2y – 2z – 7 = 0 có tâm I(-1; 1;1) và
Mặt cầu: x 2 + y 2 + z 2 + 2x + 2y + 4z + 5= 0 có tâm I’( -1; -1; -2) và R’ = 1
![]()
Do đó, hai mặt cầu này cắt nhau.
Đúng 0
Bình luận (0)
Xét vị trí tương đối của mỗi cặp đường thẳng sau
a) \({d_1}:3x + 2y--5 = 0\) và \({d_2}:x - 4y + 1 = 0\) ;
b) \({d_3}:x - 2y + 3 = 0\) và \({d_4}: - {\rm{ }}2x + 4y + 10 = 0\) ;
c) \({d_5}:4x + 2y - 3 = 0\) và \({d_6}:\left\{ \begin{array}{l}x = - \frac{1}{2} + t\\y = \frac{5}{2} - 2t\end{array} \right.\)
a) Tọa độ giao điểm của hai đường thẳng \({d_1},{d_2}\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}3x + 2y - 5 = 0\\x - 4y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{9}{7}\\y = \frac{4}{7}\end{array} \right.\)
Hệ phương trình có nghiệm duy nhất nên 2 đường thẳng cắt nhau.
b) Tọa độ giao điểm của hai đường thẳng \({d_3},{d_4}\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x - 2y + 3 = 0\\ - 2x + 4y + 10 = 0\end{array} \right.\) .
Hệ phương trình vô nghiệm.nên 2 đường thẳng song song với nhau
c) Tọa độ giao điểm của hai đường thẳng \({d_5},{d_6}\) tương ứng với t thỏa mãn phương trình:
\(4\left( { - \frac{1}{2} + t} \right) + 2\left( {\frac{5}{2} - 2t} \right) - 3 = 0 \Leftrightarrow 0t = 0\) .
Phương trình này có nghiệm với mọi t. Do đó \({d_5} \equiv {d_6}\).
Đúng 0
Bình luận (0)
Xét vị trí tương đối của đường thẳng Δ: x – 2y + 1 = 0 với mỗi đường thẳng sau:
d1: -3x + 6y – 3 = 0;
d2: y = -2x;
d3: 2x + 5 = 4y.
Xét Δ và d1, hệ phương trình: 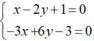 có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
Xét Δ và d2, hệ phương trình: 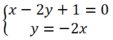 có nghiệm duy nhất (-1/5; 2/5) nên
có nghiệm duy nhất (-1/5; 2/5) nên
Δ cắt d2 tại điểm M(-1/5; 2/5).
Xét Δ và d3, hệ phương trình: 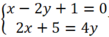 vô nghiệm
vô nghiệm
Vậy Δ // d3
Đúng 0
Bình luận (0)
Xét vị trí tương đối của các cặp đường thẳng sau
a) d:3x+y-1=0; d’:4x+2y+5=0
b) d:x-2y+5;d’:2x-4y+1=0
c) d:8x+10y-108=0;d’:4x+5y-54=0
d)d: {x=5+t ; d’:x-4/2 = y+7/3
y=-3+2t
e) d: {x=5+t ; d’:x-y-4=0
y=-1-t
xét các vị trị tương đối của mỗi cặp phẳng cho bởi các phương trình sau.
a) x+2y-z+5=0 và 2x+3y-7z-4=0
b) x-2y+z-3=0 và 2x-y+4z-2=0
c) x+y+z-1=0 và 2x+2y+2z+3=0
d) 3x-2y+3z+5=0 và 9x-6y-9z-5=0
e) x-y+2z-4=0 và 10x-10y+20z-40=0
a) Hai mặt phẳng cắt nhau, vì 1: 2: (-1) ≠ 2: 3: (-7)
b) Hai mặt phẳng cắt nhau, vì: 1: (-2): 1 ≠ 2: (-1): 4
c) Hai mặt phẳng song song, vì: 1/2=1/2=1/2 ≠ -1/3
d) Hai mạt phẳng cắt nhau, vì: 3: (-2): 3 ≠ 9: (-6): (-9)
e) Hai mặt phẳng trung nhau, vì: 1/10=-1/(-10)=2/20=-4/(-40).
#rin
Cho mp anpha: x+2y+3z-1=0 . Mp nào sau đây vuông góc với mp anpha
A. (P): 2x+4y+6z-2 =0
B. (R): 2x-4y+6z-2 = 0
C. (Q): x-1y+2z-2 = 0
D. (S): x-y+2z-3= 0
\(\overrightarrow{n_{\left(\alpha\right)}}=\left(1;2;3\right)\)
\(\overrightarrow{n_{\left(P\right)}}=\left(2;4;6\right)\)
\(\overrightarrow{n_{\left(R\right)}}=\left(2;-4;6\right)\)
\(\overrightarrow{n_{\left(Q\right)}}=\left(1;-1;2\right)\)
\(\overrightarrow{n_{\left(S\right)}}=\left(1;-1;2\right)\)
Tích vô hướng của \(\overrightarrow{n_{\left(\alpha\right)}}\) với cả 4 vecto kia đều khác 0 nên ko mặt phẳng nào vuông góc với \(\left(\alpha\right)\)
Bạn coi lại đề bài
Đúng 0
Bình luận (0)
Xét vị trí tương đối của các cặp mặt phẳng cho bởi phương trình tổng quát sau đây: ( α 3 ): x – y + 2z – 4 = 0, ( α ' 3 ): 10x − 10y + 20z – 40 = 0
Xét vị trí tương đối của cặp đường thẳng \({d_1}\)và \({d_2}\)sau đây:
a) \({d_1}:x - y + 2 = 0\) và \({d_2}:x + y + 4 = 0\)
b) \({d_1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + 5t\end{array} \right.\) và \({d_2}:5x - 2y + 9 = 0\)
c) \({d_1}:\left\{ \begin{array}{l}x = 2 - t\\y = 5 + 3t\end{array} \right.\) và \({d_2}:3x + y - 11 = 0\)
a) \({d_1}\)và \({d_2}\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {1; - 1} \right),\overrightarrow {{n_2}} = \left( {1;1} \right)\)
Ta có \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 1.1 + ( - 1).1 = 0\) nên \(\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \)
Giải hệ phương trình \(\left\{ \begin{array}{l}x - y + 2 = 0\\x + y + 4 = 0\end{array} \right.\) ta được nghiệm \(\left\{ \begin{array}{l}x = - 3\\y = - 1\end{array} \right.\)
Suy ra hai đường thẳng \({d_1}\)và \({d_2}\) vuông góc và cắt nhau tại \(M\left( { - 3; - 1} \right)\)
b) \({d_1}\)và \({d_2}\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {5; - 2} \right),\overrightarrow {{n_2}} = \left( {5; - 2} \right)\)
\(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) trùng nhau nên hai vectơ pháp tuyến cùng phương. Suy ra \({d_1}\)và \({d_2}\)song song hoặc trùng nhau
Lấy điểm \(A(1;3)\) thuộc \({d_1}\), thay tọa độ của A vào phương trình \({d_2}\), ta được \(5.1 - 2.3 + 9 = 8 \ne 0\), suy ra A không thuộc đường thẳng \({d_2}\)
Vậy hai đường thẳng \({d_1}\)và \({d_2}\) song song
c) \({d_1}\)và \({d_2}\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {3;1} \right),\overrightarrow {{n_2}} = \left( {3;1} \right)\)
Suy ra hai vectơ pháp tuyến cùng phương. Suy ra \({d_1}\)và \({d_2}\)song song hoặc trùng nhau
Lấy điểm \(A(2;5)\) thuộc \({d_1}\), thay tọa độ của A vào phương trình \({d_2}\), ta được \(3.2 + 5 - 11 = 0\), suy ra A thuộc đường thẳng \({d_2}\)
Vậy hai đường thẳng \({d_1}\)và \({d_2}\) trùng nhau
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): \(x^2+y^2+z^2-2x+6y-8z-10=0\) và mặt phẳng (P): \(x+2y-2z=0\). Viết phương trình mặt phẳng (Q) song song với (P) và tiếp xúc với (S).


















