(x-1/3)^2022+ (1/4-y)^2024 =0

Những câu hỏi liên quan
Tìm x , y biết: (2x -5)2022 + (3y +4)2024 ≤ 0
Vì : \(\left(2x-5\right)^{2022}\ge0\forall x,\left(3y+4\right)^{2024}\ge0\forall y\\ =>\left(2x-5\right)^{2022}+\left(3y+4\right)^{2024}\ge0\)
Do đó đề bài xảy ra khi và chỉ khi :
\(\left\{{}\begin{matrix}\left(2x-5\right)^{2022}=0\\\left(3y+4\right)^{2024}=0\end{matrix}\right.\\ =>\left(x;y\right)=\left(\dfrac{5}{2};-\dfrac{4}{3}\right)\)
Đúng 2
Bình luận (0)
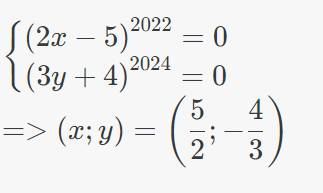 Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
Đúng 0
Bình luận (0)
(x-2022)^2024+|y-2023|< hoặc =0
\(\left(x-2022\right)^{2024}+\left|y-2023\right|\le0\left(1\right)\)
Nhận thấy : \(\left(x-2022\right)^{2024}\ge0\forall x\inℝ,\left|y-2023\right|\ge0\forall y\inℝ\)
\(=>\left(x-2022\right)^{2024}+\left|y-2023\right|\ge0\forall x,y\inℝ\)
Do đó (1) xảy ra khi :
\(\left(x-2022\right)^{2024}=0,\left|y-2023\right|=0\)
\(=>\left(x;y\right)=\left(2022;2023\right)\)
Đúng 2
Bình luận (0)
Cho em xin hỏi bài toán này ạ! Em xin cảm ơn !
1/2021×2022+1/2022×2023+1/2023×2024+1/2024×2025-4/2021×2025=
trong các cách rút gọn sau đây cách rút gọn nào là đúng đối với S=1+3 mũ 2+3 mũ 4+...+3 mũ 2022
a:3 mũ 2024:2+1 b:3 mũ 2024+1:2 c: 3 mũ 2022:2+1 d: không đáp án nào đúng
\(S=1+3^2+3^4+...+3^{2022}\)
\(3^2S=9S=3^2+3^4+3^6+...+3^{2024}\)
\(S=\dfrac{9S-S}{8}=\left(3^{2024}-1\right):8\)
d, không đáp án nào đúng
Đúng 3
Bình luận (0)
Lời giải:
$S=1+3^2+3^4+....+3^{2022}$
$9S=3^2S=3^2+3^4+3^6+...+3^{2024}$
$\Rightarrow 9S-S=3^{2024}-1$
$\Rightarrow S=\frac{3^{2024}-1}{8}$
Đáp án D.
Đúng 1
Bình luận (0)
Tìm số nguyên dương x sao cho 5x +13 là bội của 2x+1
Tìm x biết (2x-18).(3x+12)=0
Tính S= 1-2-3+4+
5-6-7+8+...+2021-2022-2023+2024+2025
1. Giải:
Do \(5x+13B\in\left(2x+1\right)\Rightarrow5x+13⋮2x+1.\)
\(\Rightarrow2\left(5x+13\right)⋮2x+1\Rightarrow10x+26⋮2x+1.\)
\(\Rightarrow5\left(2x+1\right)+21⋮2x+1.\)
Do 5(2x+1)⋮2x+1⇒ Ta cần 21⋮2x+1.
⇒ 2x+1 ϵ B(21)=\(\left\{1;3;7;21\right\}.\)
Ta có bảng:
| 2x+1 | 1 | 3 | 7 | 21 |
| x | 0 | 1 | 3 | 10 |
| TM | TM | TM | TM |
Vậy xϵ\(\left\{0;1;3;10\right\}.\)
2. Giải:
Do (2x-18).(3x+12)=0.
⇒ 2x-18=0 hoặc 3x+12=0.
⇒ 2x =18 3x =-12.
⇒ x =9 x =-4.
Vậy xϵ\(\left\{-4;9\right\}.\)
3. S= 1-2-3+4+5-6-7+8+...+2021-2022-2023+2024+2025.
S= (1-2-3+4)+(5-6-7+8)+...+(2021-2022-2023+2024)+2025 Có 506 cặp.
S= 0 + 0 + ... + 0 + 2025.
⇒S= 2025.
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của các bthuc sau
vd; P=x^2-2x+2023
= x^2-2x.1+2022
tại (x-1)^2 lớn hơn/bằng 0, với mọi x
=> (x-1)^2+2022 lớn hơn hoặc bằng 2022 với mọi x
vậy P đạt giá trị nhỏn nhất bằng 2022 kkhi x=1
BT:
P=x^2+2x-2024
P = (x^2 + 2x) - 2024
= (x^2 + 2x + 1) - 1 - 2024
= (x + 1)^2 - 2025
Với mọi giá trị của x, (x + 1)^2 luôn lớn hơn hoặc bằng 0. Do đó, giá trị nhỏ nhất của P là khi (x + 1)^2 đạt giá trị nhỏ nhất, tức là bằng 0.
Khi (x + 1)^2 = 0, ta có x + 1 = 0, từ đó suy ra x = -1.
Vậy, giá trị nhỏ nhất của biểu thức P là P = (-1 + 1)^2 - 2025 = -2025.
Đúng 0
Bình luận (0)
\(P\left(x\right)\)=\(x^{2023}-2024.x^{2022}+2024.x^{2021}-2024.x^{2020}+.....+2024.x-1\)
tính P ( 2023)
Giải nhanh giúp mik ạ !! đang cânf gấp O(∩_∩)O
Với x = 2023
<=> x + 1 = 2024
Khi đó P(2023) = x2023 - (x + 1).x2022 + ... + (x + 1).x - 1
= x2023 - x2023 - x2022 + .. + x2 + x - 1
= x - 1 = 2023 - 1 = 2022
Đúng 1
Bình luận (0)
Tìm x:
a) (2x - 5)2022
b) (3x + 4)2024
Có thể đưa ra lời giải cụ thể ko ạ, 0-0
a,Nghiệm của (2\(x\) - 5)2022 là giá trị của \(x\) thỏa mãn
(2\(x\) - 5)2022 = 0
2\(x\) - 5 = 0
2\(x\) = 5
2\(x\) = 5:2
\(x\) = 2,5
b, Nghiệm của (3\(x\) + 4)2024 là giá trị của \(x\) thỏa mãn:
(3\(x\) + 4)2024 = 0
3\(x\) + 4 = 0
3\(x\) = -4
\(x\) = - 4 : 3
\(x\) = -\(\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
1) Tính hợp lý :
P=1-2-3+4+5-6-7+8+.........+2021-2022-2023+2024
P=[(1-2)+(-3+4)+(5-6)+(-7+8)+...+(993-994)+(-995+996)]+997
P=[(-1)+1+(-1)+1+...+(-1)+1+(-1)+1]+997
P= 0 +0 +...+ 0 +997
P=997
Đúng 0
Bình luận (0)



















