tìm xác xuất để 2 người gặp ngẫu nhiên ngoài đường trùng sinh nhâtj nhau . giả sử 1 năm 365

Những câu hỏi liên quan
tìm xác suất để 2 người gặp ngẫu nhiên ngoài đường trùng sinh nhâtj nhau . (giả sử 1 năm 365)
Biến cố đối là hai người này có ngày sinh khác nhau
=>Xác suất của biến cố là: \(1-\dfrac{364\cdot365}{365^2}=1-\dfrac{364}{365}=\dfrac{1}{365}\)
Đúng 0
Bình luận (0)
Trong chương trình giao lưu gồm có 15 người ngồi vào 15 ghế theo một hàng ngang. Giả sử người dẫn chương trình chọn ngẫu nhiên 3 người trong 15 người để giao lưu với khán giả. Xác suất để trong 3 người được chọn đó không có 2 người ngồi kề nhau A.
2
5
B.
13
35
C.
22
35
D.
3
5
Đọc tiếp
Trong chương trình giao lưu gồm có 15 người ngồi vào 15 ghế theo một hàng ngang. Giả sử người dẫn chương trình chọn ngẫu nhiên 3 người trong 15 người để giao lưu với khán giả. Xác suất để trong 3 người được chọn đó không có 2 người ngồi kề nhau
A. 2 5
B. 13 35
C. 22 35
D. 3 5
Trong chương trình giao lưu gồm có 15 người ngồi vào 15 ghế theo một hàng ngang. Giả sử người dẫn chương trình chọn ngẫu nhiên 3 người trong 15 người để giao lưu với khán giả. Xác suất để trong 3 người được chọn đó không có 2 người ngồi kề nhau A.
2
5
B.
13
35
C.
22
35
D.
3
5
Đọc tiếp
Trong chương trình giao lưu gồm có 15 người ngồi vào 15 ghế theo một hàng ngang. Giả sử người dẫn chương trình chọn ngẫu nhiên 3 người trong 15 người để giao lưu với khán giả. Xác suất để trong 3 người được chọn đó không có 2 người ngồi kề nhau
A. 2 5
B. 13 35
C. 22 35
D. 3 5
Trong chương trình giao lưu gồm có 15 người ngồi vào 15 ghế theo một hàng ngang. Giả sử người dẫn chương trình chọn ngẫu nhiên 3 người trong 15 người để giao lưu với khán giả. Xác suất để trong 3 người được chọn đó không có 2 người ngồi kề nhau là
A
.
2
5
B
.
13
35
C
.
22
35...
Đọc tiếp
Trong chương trình giao lưu gồm có 15 người ngồi vào 15 ghế theo một hàng ngang. Giả sử người dẫn chương trình chọn ngẫu nhiên 3 người trong 15 người để giao lưu với khán giả. Xác suất để trong 3 người được chọn đó không có 2 người ngồi kề nhau là
A . 2 5
B . 13 35
C . 22 35
D . 3 5
Chọn C
Ta có: ![]()
Gọi A là biến cố “trong 3 người được chọn đó không có 2 người ngồi kề nhau”
=> A ¯ là biến cố “trong 3 người đươc chọn có ít nhất 2 người ngồi kề nhau”
![]()

TH 1: 3 người ngồi kề nhau có 13 cách chọn.
TH 2: có 2 người ngồi cạnh nhau
- Hai người ngồi cạnh nhau ngồi đầu hàng có 2 cách chọn, với mỗi cách chọn như vậy có 12 cách chọn người còn lại vậy có: 2.12=24 cách.
- Hai người ngồi cạnh nhau không ngồi đầu hàng có 12 cách chọn, với mỗi cách chọn như vậy có 11 cách chọn người còn lại vậy có: 11.12=132 cách.
![]()
Đúng 0
Bình luận (0)
Hai người hẹn gặp nhau tại thư viện từ 8 giờ đến 9 giờ. Người đến trước đợi quá 10 phút mà không gặp thì rời đi. Tìm xác suất để hai người đi ngẫu nhiên mà gặp nhau? A.
7
36
B.
11
36
C.
10
36
D.
13
36
Đọc tiếp
Hai người hẹn gặp nhau tại thư viện từ 8 giờ đến 9 giờ. Người đến trước đợi quá 10 phút mà không gặp thì rời đi. Tìm xác suất để hai người đi ngẫu nhiên mà gặp nhau?
A. 7 36
B. 11 36
C. 10 36
D. 13 36
Hai người hẹn gặp nhau tại thư viện từ 8 giờ đến 9 giờ. Người đến trước đợi quá 10 phút mà không gặp thì rời đi. Tìm xác suất để hai người đi ngẫu nhiên mà gặp nhau? A. B. C. D.
Đọc tiếp
Hai người hẹn gặp nhau tại thư viện từ 8 giờ đến 9 giờ. Người đến trước đợi quá 10 phút mà không gặp thì rời đi. Tìm xác suất để hai người đi ngẫu nhiên mà gặp nhau?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án B.
Gọi x (phút) là thời gian mà bạn A đến chờ ở thư viện.
Gọi y (phút) là thời gian mà bạn B đến chờ ở thư viện.
Điều kiện: ![]()
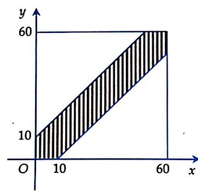
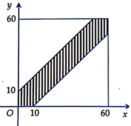
![]() (là diện tích hình vuông cạnh 60)
(là diện tích hình vuông cạnh 60)
Điều kiện gặp nhau là
![]() (*)
(*)
Do điểm ![]() thỏa điều kiện (*) thuộc lục giác gạch sọc giới hạn bởi 2 đường thẳng
thỏa điều kiện (*) thuộc lục giác gạch sọc giới hạn bởi 2 đường thẳng ![]() là hình vuông của không gian mẫu.
là hình vuông của không gian mẫu.
Lục giác có diện tích
![]()
Vậy xác suất để 2 người gặp nhau là:
![]()
Đúng 0
Bình luận (0)
Một bài trắc nghiệm có 10 câu hỏi ,mỗi câu có 4 phương án lựa chọn trong đó có một đáp án đúng . Giả sử mỗi câu trả lời đúng được 5 điểm sai bị trừ 2 điểm . Một học sinh không học bài nên chọn ngẫu nhiên một phương án . Tính xác xuất để học sinh nhận điểm dưới 1
Giả sử học sinh đó chọn x câu đúng (với \(0\le x\le10\)), như vậy sẽ có \(10-x\) câu sai
Số điểm học sinh đó đạt được là:
\(5x-2\left(10-x\right)=7x-20\)
Điểm dưới 1 \(\Rightarrow7x-20< 1\Rightarrow x< 3\)
Vậy học sinh đó trả lời đúng 0,1 hoặc 2 câu
Xác suất đúng khi chọn mỗi câu hỏi là 1/4 còn xác suất sai là 3/4 nên xác suất học sinh đó dưới 1 điểm là:
\(C_{10}^0.\left(\dfrac{1}{4}\right)^0.\left(\dfrac{3}{4}\right)^{10-0}+C_{10}^1.\left(\dfrac{1}{4}\right)^1.\left(\dfrac{3}{4}\right)^{10-1}+C_{10}^2.\left(\dfrac{1}{4}\right)^2.\left(\dfrac{3}{4}\right)^{10-2}=...\)
Đúng 3
Bình luận (1)
Thế hệ xuất phát của một quần thể ngẫu phối có 0,5AA : 0,4Aa : 0,1aa. Giả sử kiểu hình lặn (aa) không có khả năng sinh sản. Ở thế hệ F3, lấy ngẫu nhiên 2 cá thể, xác suất thu được 2 cá thể có kiểu gen dị hợp là bao nhiêu?
A. 0,025
B. 0,065
C. 0,038
D. 0,13
Tần số alen ở thế hệ xuất phát là: a = 0,22
Tần số alen ở thế hệ F2 là: a = q/(1+2q) = 0,15; A = 1 - 0,15 = 0,85
Tỉ lệ kiểu gen ở F3=0,852AA+2.0,85.0,15Aa+0,152aa=1
Tỉ lệ kiểu gen dị hợp là 2.0,85.0,15 = 0,255; tỉ lệ kiểu gen đồng hợp = 1 - 0,255= 0,745
Vậy lấy ngẫu nhiên 2 cá thể ở F3, xác xuất thu được cả 2 cá thể có kiểu gen dị hợp là:
0,255×0,255 = 0,065
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
để chuẩn bị thi một sinh viên được cho hai tập câu hỏi để ôn tập mỗi tập gồm 10 câu. Giả sử trước khi thi anh ta học thuộc 9 câu của tập 1 và 8 câu ở tập 2. Để thi gồm 3 câu thiết kế như sau: Chọn ngẫu nhiên một tập câu hỏi rồi ngẫu nhiên chọn 2 câu . Câu thứ 3 chọn ngẫu nhiên từ tập còn lại. Tính xác suất để sinh viên trả lời đúng 2 câu.